
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{11}{26}+\dfrac{32}{39}-\left(-\dfrac{14}{52}\right)\)
=\(\dfrac{97}{78}+\dfrac{14}{52}\)
=\(\dfrac{59}{39}\)



\(A=1^2+2^2+3^2+....+10^2\\ A=1^{ }+\left(1+1\right)\cdot2+3\cdot\left(2+1\right)+.....+10\cdot\left(9+1\right)\\ A=1+2\cdot1+2+3\cdot2+3+....+10\cdot9+10\\ A=\left(1+2+3...+10\right)+\left(1\cdot2+3\cdot2+.....+10\cdot9\right)\)
Gọi 1+2+3+...+10 là P
Số số hạng là: (10 - 1) : 1 +1 = 10 (số)
P = (10+1) . 10 : 2 = 55
P = 55
Gọi \(1\cdot2+2\cdot3+....+9\cdot10\) là C
\(C=1\cdot2+2\cdot3+....+9\cdot10\\ 3\cdot C=1\cdot2\cdot3+2\cdot3\cdot3+....+9\cdot10\cdot3\\ 3\cdot C=1\cdot2\cdot3+2\cdot3\cdot\left(4-1\right)+....+9\cdot10\cdot\left(11-8\right)\\ 3\cdot C=1\cdot2\cdot3+2\cdot3\cdot4-1\cdot2\cdot3+.....+9\cdot10\cdot11-8\cdot9\cdot10\\ 3\cdot C=9\cdot10\cdot11\\ 3\cdot C=990\\ C=330\)
\(=>A=P+C\\ =>A=55+330\\ A=385\)
b)
\(B=5^2+10^2+15^2+...+50^2\\ B=5^2+\left(2\cdot5\right)^2+\left(3\cdot5\right)^2+....+\left(5\cdot10\right)^2\\ B=5^2+2^2\cdot5^2+3^2\cdot5^2+...+5^2\cdot10^2\\ B=5^2\cdot\left(1+2^2+3^2+....+10^2\right)\\ B=25\cdot\left(1+2^2+3^2+....+10^2\right)\)
\(\left(1+2^2+3^2+....+10^2\right)=A\)
\(=>B=25\cdot A\\ B=25\cdot385\\ B=9625\)

https://olm.vn/cau-hoi/a-cho-a12211216211002-ctr-a12-b-cho-p122132142120232-ctr-p-khong-la-so-tu-nhien-c-cho-c132152172120211.8293222842881
Cô làm rồi em nhá

Câu a, xem lại đề bài
Câu b:
P = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{4^2}\) + ...+ \(\dfrac{1}{2023^2}\)
Vì \(\dfrac{1}{2^2}\) < \(\dfrac{1}{1.2}\) = \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\)
\(\dfrac{1}{3^2}\) < \(\dfrac{1}{2.3}\) = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)
\(\dfrac{1}{4^2}\) < \(\dfrac{1}{3.4}\) = \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\)
........................
\(\dfrac{1}{2023^2}\) < \(\dfrac{1}{2022.2023}\) = \(\dfrac{1}{2022}\) - \(\dfrac{1}{2023}\)
Cộng vế với vế ta có:
0< P < 1 - \(\dfrac{1}{2023}\) < 1
Vậy 0 < P < 1 nên P không phải là số tự nhiên vì không tồn tại số tự nhiên giữa hai số tự nhiên liên tiếp
Câu c:
C = \(\dfrac{1}{3^2}\) + \(\dfrac{1}{5^2}\) + \(\dfrac{1}{7^2}\) + ....+ \(\dfrac{1}{2021^2}\) + \(\dfrac{1}{2023^2}\) = C
B = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{4^2}\) + \(\dfrac{1}{6^2}\)+.......+ \(\dfrac{1}{2020^2}\) + \(\dfrac{1}{2023^2}\) > 0
Cộng vế với vế ta có:
C+B = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + \(\dfrac{1}{4^2}\) + \(\dfrac{1}{5^2}\)+ \(\dfrac{1}{6^2}\)+...+ \(\dfrac{1}{2023^2}\) > C + 0 = C > 0
Mặt khác ta có:
1 > \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\)+...+ \(\dfrac{1}{2023^2}\) (cm ở ý b)
Vậy 1 > C > 0 hay C không phải là số tự nhiên (đpcm)


3 câu đầu bn Võ Quang Huy lm đúng nhưng câu cuối là bằng -22 nhé bn

a) x+ 22 + ( -14) + 52
=x+22 - 14 + 52
= x+(22+52-14)
=x+ (74-14)
=x + 60
b)(-90) - ( p + 10) + 100
=-90 - p - 10+100
=(-90 - 10 + 100) - p
=(-100 +100) - p
= -p

a) -48 + (-35 + 19) - (32 + 45 + 21)
= -48 - 35 + 19 - 32 - 45 - 21
= (-48 - 32) - (35 + 45) + (19 - 21)
= -80 - 80 - 2
= -162
b) -47 + (38 - 13) - (-52 + 31 - 91)
= -47 + 38 - 13 + 52 - 31 + 91
= (-47 - 13) + (38 + 52) - 31
= -60 + 90 - 31
= 30 - 31 = -1
c) 54 + (-37) - (+70) + (-163) - (-246) + (-230
= 54 - 37 - 70 - 163 + 246 - 230
= (54 + 246) - (37 + 163) - (70 + 230)
= 300 - 200 - 300
= -200
còn lại tự lm
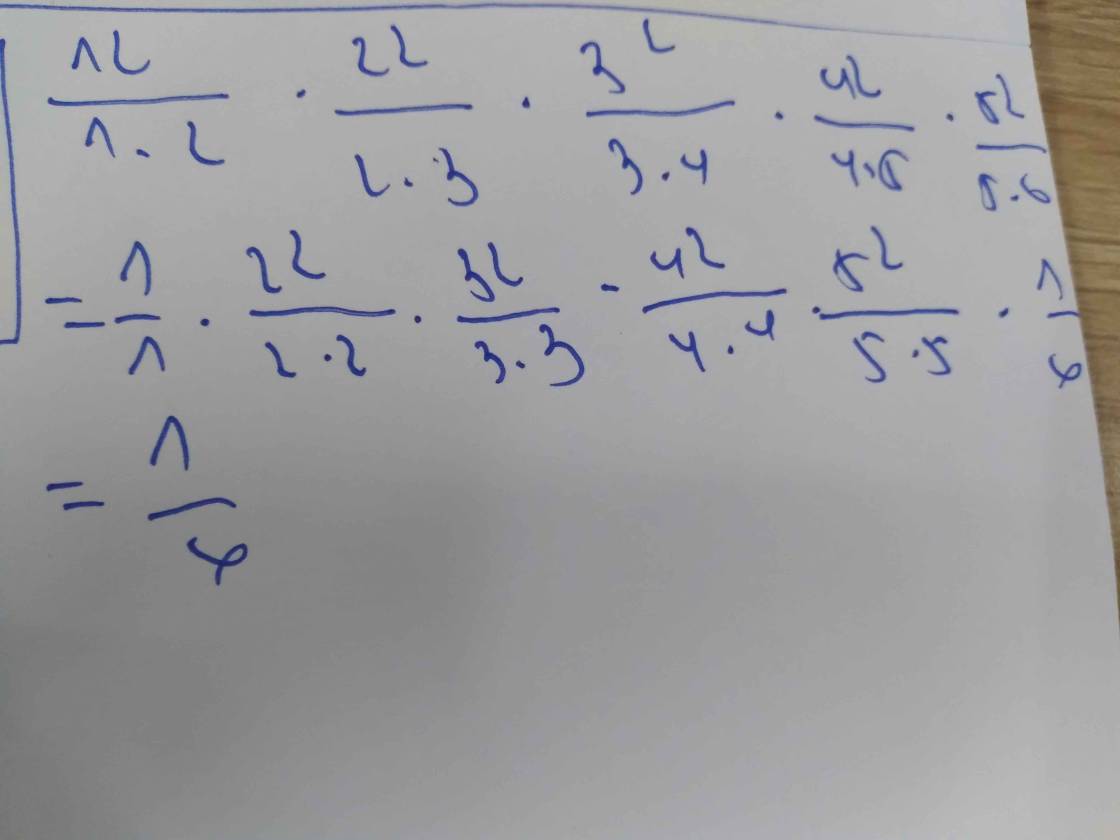
C=2^2+3^2+4^2+5^2+.... +50^2
C=(2+3+4+5+... +50) ^2
Tập C có số số hạng là :
(50-2) :2+1=25 số
=>C=[(50+2) ×25÷2]^2
C=650^2
C=422500