Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hai tam giác vuông ABC và CDB, ta có:
∠ (BAC) = ∠ (DCB) = 90 0 (1)
Mà: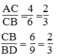
Suy ra: 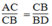 (2)
(2)
Từ (1) và (2) suy ra: △ ABC đồng dạng △ CDB (cạnh huyền và cạnh góc vuông tỉ lệ)
Suy ra: ∠ (ACB) = ∠ (CBD)
⇒ BD//AC ( hai góc ở vị trí so le trong bằng nhau )

áp dụng định lý pitago vào tam giác vuông ABC:
\(AB^2\)+\(AC^2_{ }=BC^2\)
=>\(AB^2=BC^2-AC^2\)
<=>\(AB^2=6^2-4^2=20=>AB=\sqrt[]{20}\)
ÁP dụng định lý pitago vào tam giác vuông BCD
\(BC^2+DC^2=BD^2=>DC^2=BD^2-BC^2=9^2-6^2=45=>DC=\sqrt[]{45}\)
TA CÓ
\(\dfrac{AB}{CD}=\dfrac{\sqrt[]{20}}{\sqrt[]{45}}=\dfrac{2}{3}\) (1)
\(\dfrac{DC}{BC}=\dfrac{6}{9}=\dfrac{2}{3}\) (2)
TỪ 1 và 2 => \(\Delta ABC\sim\Delta BCD\)
=>\(\widehat{DBC}=\widehat{ACB}\) mà 2 góc này ở vị trí so le trong => BD//AC

a: Xét ΔBAC vuông tại A và ΔDCB vuông tại C có
BA/DC=AC/CB
=>ΔBAC đồng dạng với ΔDCB
b: ΔBAC đồng dạng với ΔDCB
=>góc ACB=góc CBD
=>AC//BD

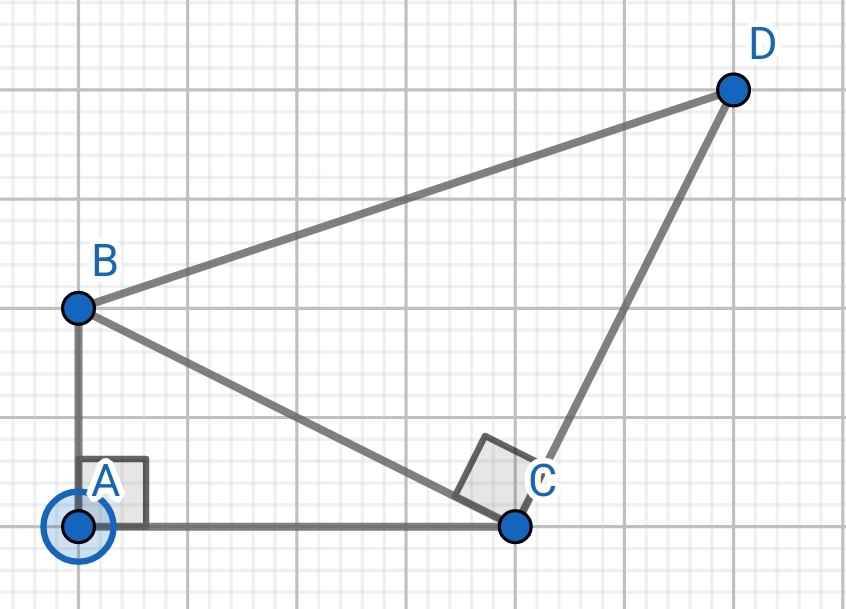
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
⇒ AB² = BC² - AC²
= 12² - 8²
= 80
⇒ AB = \(4\sqrt{5}\) (cm)
∆CDB vuông tại C
⇒ BD² = CD² + BC² (Pytago)
⇒ CD² = BD² - BC²
= 18² - 12²
= 180
⇒ CD = \(6\sqrt{5}\) (cm)
Xét ∆ABC và ∆CDB có:
\(\dfrac{BC}{BD}=\dfrac{12}{18}=\dfrac{2}{3}\)
\(\dfrac{AB}{CD}=\dfrac{4\sqrt{5}}{6\sqrt{5}}=\dfrac{2}{3}\)
\(\dfrac{AC}{BC}=\dfrac{8}{12}=\dfrac{2}{3}\)
⇒ \(\dfrac{BC}{BD}=\dfrac{AB}{CD}=\dfrac{AC}{BC}=\dfrac{2}{3}\)
Vậy ∆ABC ∽ ∆CDB (c-c-c)
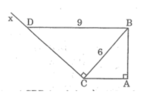



làm hộ mk với