
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`(-3737)/(4141)=(-37xx101)/(41xx101)=(-37)/41`
Vì `37/41>34/41`
`=>(-37)/41<(-34)/41`
Hay `(-3737)/(4141)<(-34)/41`
\(\dfrac{-3737}{4141}=\dfrac{-37\cdot101}{41\cdot101}=\dfrac{-37}{41}\)
Mà \(\dfrac{-37}{41}< \dfrac{-34}{41}\) (vì \(-37< -34\))
Nên \(\dfrac{-3737}{4141}< \dfrac{-34}{41}\)

a: \(\dfrac{-2}{37}=\dfrac{-82}{37\cdot41}\)
\(\dfrac{-3}{41}=\dfrac{-3\cdot37}{41\cdot37}=\dfrac{-111}{41\cdot37}\)
mà -82>-111
nên \(-\dfrac{2}{37}>-\dfrac{3}{41}\)
b: \(\dfrac{57}{47}=1+\dfrac{10}{47}\)
\(\dfrac{557}{547}=1+\dfrac{10}{547}\)
mà 10/47>10/547
nên \(\dfrac{57}{47}>\dfrac{557}{547}\)
hay \(-\dfrac{57}{47}< -\dfrac{557}{447}\)
c: \(\dfrac{139}{155}=1-\dfrac{16}{155}\)
\(\dfrac{141}{157}=1-\dfrac{16}{157}\)
mà 16/155>16/157
nên \(\dfrac{139}{155}< \dfrac{141}{157}\)


Có: \(3^{41}=3\cdot3^{40}=3\cdot\left(3^2\right)^{20}=3\cdot9^{20}\)
và \(2^{61}=2\cdot2^{60}=2\cdot\left(2^3\right)^{20}=2\cdot8^{20}\)
Lại có: \(3>2\)và \(9>8\)
\(\Leftrightarrow3>2\) và \(9^{20}>8^{20}\)\(\Leftrightarrow3\cdot3^{20}>2\cdot2^{20}\)\(\Leftrightarrow3^{41}>2^{61}\)

So sánh (-514)19 và (-14)41
Ta xét: 51419 và 1441
51419 > 51219 = 2171
1441 < 1641 = 2164
Ta có: 1441 < 1641 < 51219 < 51419
Do đó 1441 < 51419
< = > (-14)41 > (-514)19

Ta thấy:
\(11^{1979}< 11^{1980}\)
\(11^{1980}=\left(11^3\right)^{660}=1331^{660}\)
Và:
\(37^{1320}=\left(37^2\right)^{660}=1369^{660}\)
Mà: \(1331^{660}< 1369^{660}\)
\(\Rightarrow11^{1979}< 37^{1320}\)
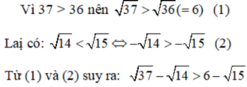
- \(\dfrac{3737}{4141}\) = - \(\dfrac{3737:101}{4141:101}\) = \(\dfrac{-37}{41}\)
vậy - \(\dfrac{3737}{4141}=-\dfrac{37}{41}\)
bằng nhau