
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


xét hthang ABCD có :E là trung điểm của AD và F là t/đ của BC => EF là đg trung bình của hthang ABCD=>EF=(AB+CD)/2
=>2EF=AB+CD (1)
+) chu vi hthang ABCD= AB +CD+AD+BC=AB +CD+2ED+2FC(vì E là t/đ của AD,F là t/đ của BC) (2)
thay (1) vào (2) ta đc: CV hthang ABCD=2(EF+DE+FC)=2.5=10cm(vì È+DE+FC=5cm)


Do ABCD là hình thang cân
\(\Rightarrow AD=BC\) và \(\widehat{FDA}=\widehat{FCB}\)
Do F là trung điểm của CD (gt)
\(\Rightarrow FC=FD\)
Xét \(\Delta ADF\) và \(\Delta BCF\) có:
\(AD=BC\) (cmt)
\(\widehat{FDA}=\widehat{FCB}\) (cmt)
\(FD=FC\) (cmt)
\(\Rightarrow\Delta ADF=\Delta BCF\) (c-g-c)
\(\Rightarrow AF=BF\) (hai cạnh tương ứng)
\(\Delta FAB\) có:
\(AF=BF\) (cmt)
\(\Rightarrow\Delta FAB\) cân tại F
Lại có E là trung điểm của AB
\(\Rightarrow FE\) là đường trung tuyến của \(\Delta FAB\)
\(\Rightarrow FE\) cũng là đường cao của \(\Delta FAB\)
\(\Rightarrow FE\perp AB\)
Mà AB // CD (gt)
\(\Rightarrow FE\perp CD\)
Vậy EF vuông góc với AB và CD

Gọi O là giao điểm của AC và BD.
Chứng minh: OE ^ AB.
Tương tự, có OF ^ CD.
Suy ra OF ^ AB. Vậy EF ^ AB

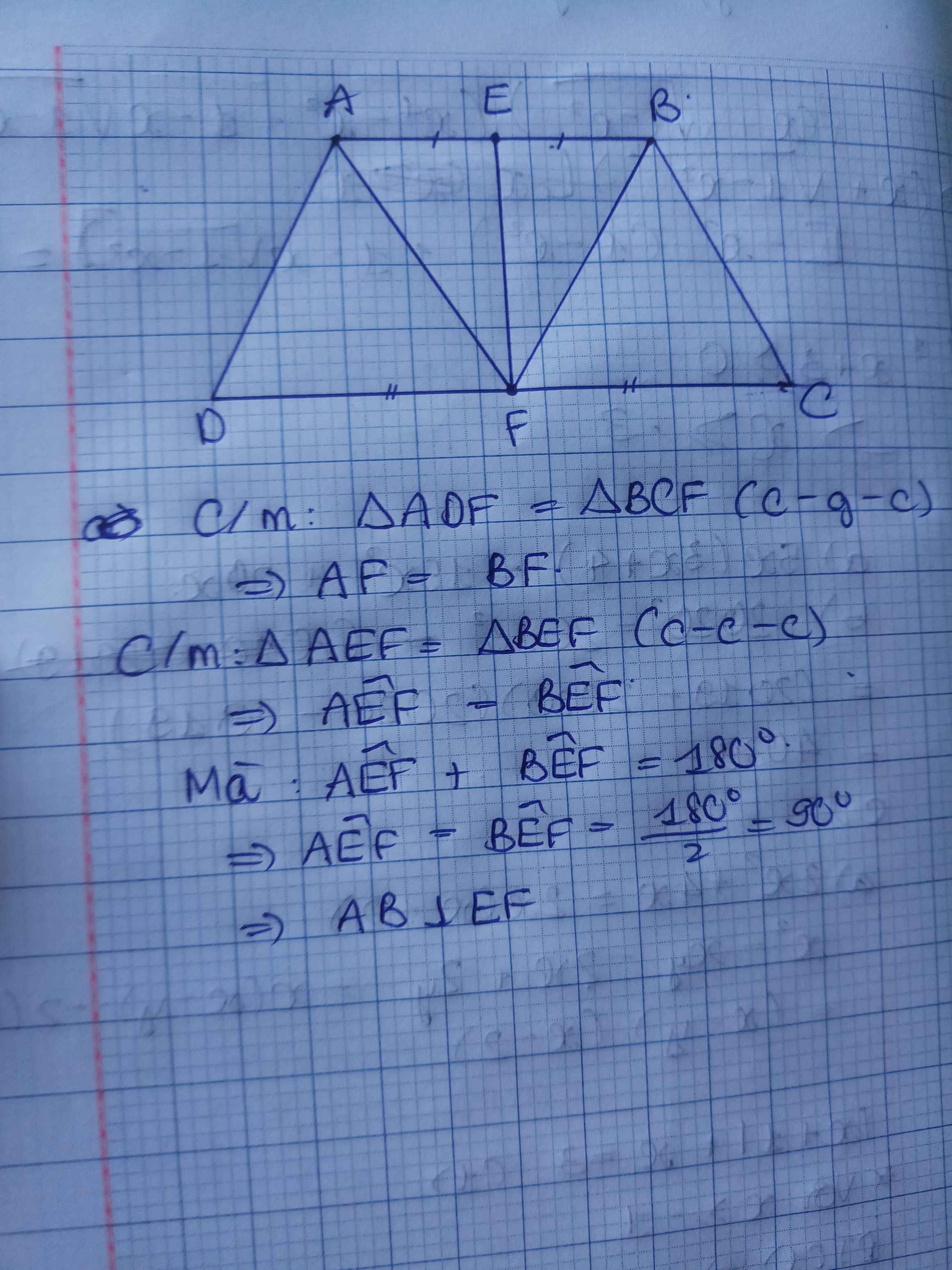
Xét ΔADF và ΔBCF có
AD=BC
\(\widehat{D}=\widehat{C}\)
FD=FC
Do đó: ΔADF=ΔBCF
Suy ra: FA=FB
Xét ΔFAB có FA=FB
nên ΔFAB cân tại F
mà FE là đường trung tuyến ứng với cạnh đáy AB
nên FE là đường cao ứng với cạnh AB
hay FE\(\perp\)AB

Ta có CD//EF
\(\Rightarrow\widehat{C}+\widehat{F}=180^0\)
Ta lại có: \(\Rightarrow\widehat{C}-\widehat{F}=66^0\)nên ta có hệ
\(\left\{{}\begin{matrix}\widehat{C}+\widehat{F}=180^0\\\widehat{C}-\widehat{F}=66^0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{C}=123^0\\\widehat{F}=57^0\end{matrix}\right.\)