K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KV
6 tháng 11 2023
A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... 2¹⁶) ⋮ 5
Vậy A ⋮ 5
16 tháng 4 2020
CÂU 10:
a, -x - 84 + 214 = -16 b, 2x -15 = 40 - ( 3x +10 )
x = - ( -16 -214 + 84 ) 2x + 3x = 40 -10 +15
x = 16 + 214 - 84 5x = 45
x = 146 x = 9
c, \(|-x-2|-5=3\) d, ( x - 2)(2x + 1) = 0
\(|-x-2|=8\) => x - 2 = 0 hoặc 2x + 1 = 0
=> - x - 2 = 8 hoặc x + 2 = 8 \(\orbr{\begin{cases}x-2=0\\2x+1=0\end{cases}=>}\orbr{\begin{cases}x=2\\x=-\frac{1}{2}\end{cases}}\)
\(\orbr{\begin{cases}-x-2=8\\x+2=8\end{cases}=>\orbr{\begin{cases}x=-10\\x=6\end{cases}}}\)
TH
5
9 tháng 1 2022
\(\left(n-4\right)⋮\left(n-1\right)\Rightarrow\left(n-1-3\right)⋮\left(n-1\right)\)
\(Mà\left(n-1\right)⋮\left(n-1\right)\Rightarrow-3⋮\left(n-1\right)\Rightarrow n-1\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\Rightarrow n\in\left\{-2;0;2;4\right\}\)
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Gọi 6 số đó là:
\(x,\left(x+1\right),\left(x+2\right),\left(x+3\right),\left(x+4\right),\left(x+5\right)\)
Mà: \(x\left(x+1\right)\) là hai số tự nhiên liên tiếp nên sẽ chia hết cho 2
\(\left(x+2\right)\left(x+3\right)\) là hai số tự nhiên liên tiếp nên sẽ chia hết cho 2
\(\Rightarrow x\left(x+1\right)\left(x+2\right)\left(x+3\right)\) chia hết cho 2.2 = 4
Mà: \(x\left(x+1\right)\left(x+2\right)\) chia hết cho 3
\(x\left(x+1\right)\left(x+2\right)\left(x+3\right)\) sẽ chia hết cho 4.3 = 12
Và: \(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)\) sẽ chia hết cho 4 nên
\(x\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)\) sẽ chia hết cho 12.4 = 48
XO
16 tháng 4 2023
a) Ta có : \(A=\dfrac{x^2+y^2+5}{x^2+y^2+3}=1+\dfrac{2}{x^2+y^2+3}\)
Dễ thấy \(x^2\ge0;y^2\ge0\forall x;y\)
nên \(x^2+y^2+3\ge3\)
\(\Leftrightarrow\dfrac{1}{x^2+y^2+3}\le\dfrac{1}{3}\)
<=> \(\dfrac{2}{x^2+y^2+3}\le\dfrac{2}{3}\)
\(\Leftrightarrow A=1+\dfrac{2}{x^2+y^2+3}\le\dfrac{5}{3}\)
\(\Rightarrow A_{max}=\dfrac{5}{3}\)(Dấu "=" xảy ra khi x = y = 0)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 12 2023
Câu 1: Vì p và 10p + 1 là các số nguyên tố lớn hơn 3 nên p ≠ 2 vậy p là các số lẻ.
Ta có: 10p + 1 - p = 9p + 1
Vì p là số lẻ nên 9p + 1 là số chẵn ⇒ 9p + 1 = 2k
17p + 1 = 8p + 9p + 1 = 8p + 2k = 2.(4p + k) ⋮ 2
⇒ 17p + 1 là hợp số (đpcm)
AH
Akai Haruma
Giáo viên
28 tháng 12 2023
Câu 1:
Vì $p$ là stn lớn hơn $3$ nên $p$ không chia hết cho $3$. Do đó $p$ có dạng $3k+1$ hoặc $3k+2$.
Nếu $p=3k+2$ thì:
$10p+1=10(3k+2)+1=30k+21\vdots 3$
Mà $10p+1>3$ nên không thể là số nguyên tố (trái với giả thiết)
$\Rightarrow p$ có dạng $3k+1$.
Khi đó:
$17p+1=17(3k+1)+1=51k+18=3(17k+6)\vdots 3$. Mà $17p+1>3$ nên $17p+1$ là hợp số
(đpcm)
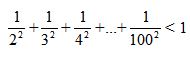
Ta có:
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{100}\)
Mà \(1-\dfrac{1}{100}< 1\)
\(=>\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< 1\)
122+132+142+...+11002<11.2+12.3+13.4+...+199.100122+132+142+...+11002<11.2+12.3+13.4+...+199.100
122+132+142+...+11002<1−12+12−13+13−14+...+199−1100122+132+142+...+11002<1−12+12−13+13−14+...+199−1100
122+132+142+...+11002<1−1100122+132+142+...+11002<1−1100
Mà 1−1100<11−1100<1
=>122+132+142+...+11002<1