
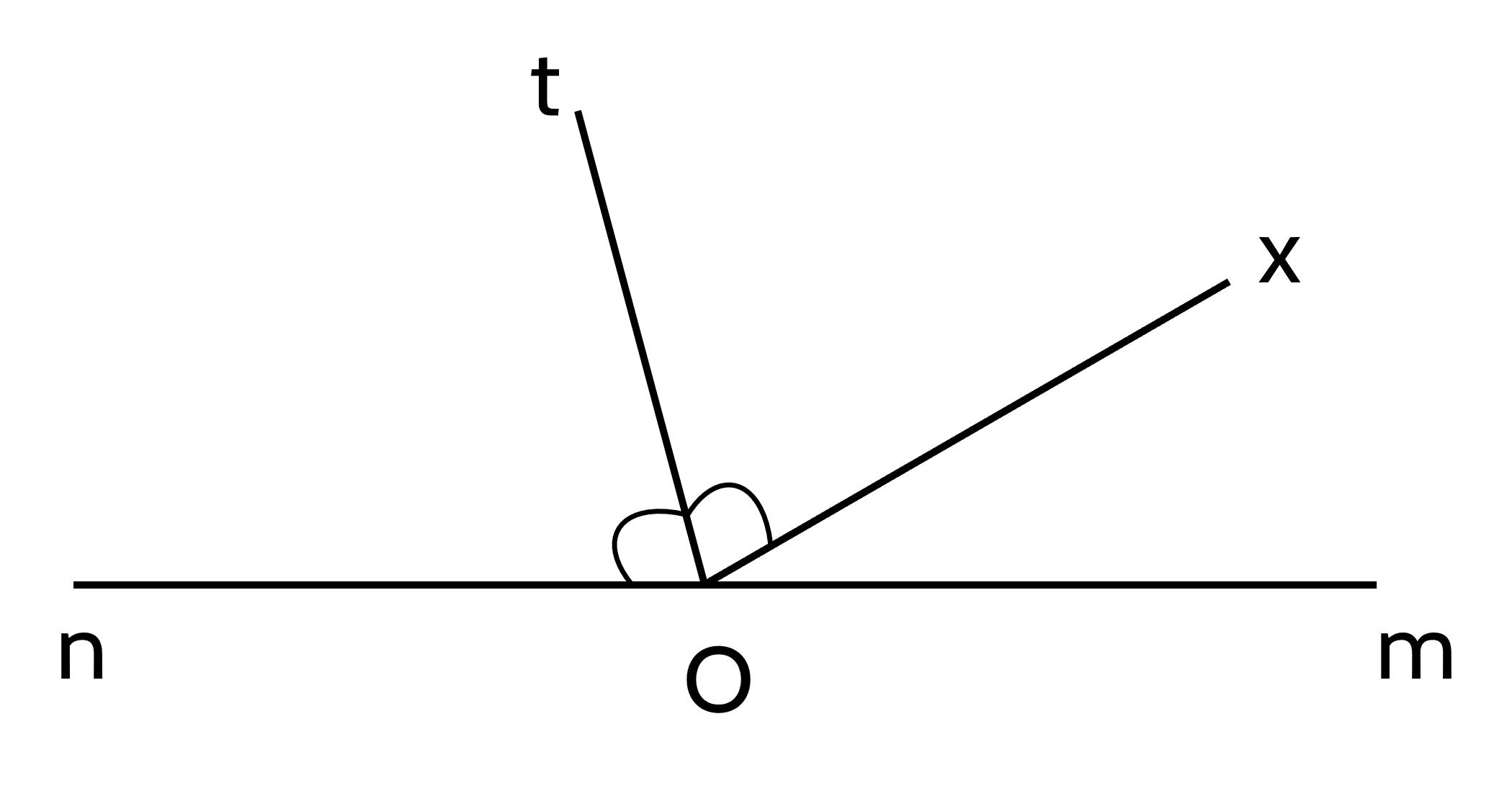
a) Ta có:
∠mOx + ∠nOx = 180⁰ (kề bù)
⇒ ∠nOx = 180⁰ - ∠mOx
= 180⁰ - 30⁰
= 150⁰
Do Ot là tia phân giác của ∠nOx
⇒ ∠nOt = ∠nOx : 2
= 150⁰ : 2
= 75⁰
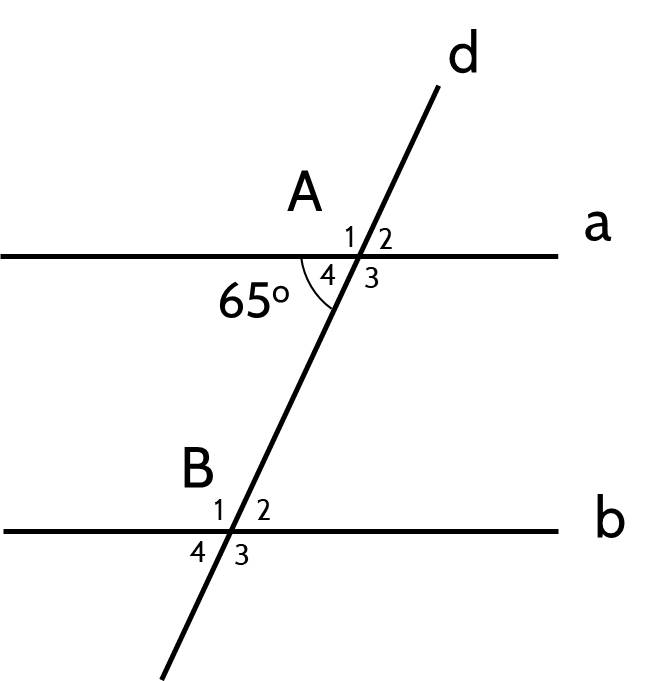
b) Do a // b
⇒ ∠B₄ = ∠A₄ = 65⁰ (đồng vị)
Ta có:
∠B₃ + ∠B₄ = 180⁰ (kề bù)
⇒ ∠B₃ = 180⁰ - ∠B₄
= 180⁰ - 65⁰
= 115⁰
Tính số đo góc �3^B3.
Hướng dẫn giải:a) ���^+���^=180∘mOx+xOn=180∘
Vậy ���^=180∘−30∘=150∘nOx=180∘−30∘=150∘.
��Ot là tia phân giác của ���^nOx, suy ra ���^=12.���^=75∘nOt=21.nOx=75∘.
b) a // b suy ra �4^=�2^=65∘A4=B2=65

\(a)d\perp m,ab\perp m\Leftrightarrow d//ab\)( từ vuông góc đến song song)
\(b)\widehat{ABA}=60^0\)( câu này bạn tự tính )
\(c)\widehat{HBA}=\frac{\widehat{ABa}}{2}=\frac{120^0}{2}=60^0\)và \(\widehat{HAB}=60^0\)
\(\Rightarrow\widehat{AHB}=60^0\)
\(d)\)Vì Ba là tia đối của BN nên \(\widehat{ABA},\widehat{CBN}\)là 2 góc đối nhau nên 2 tia phân giác của nó đối nhau hay BH và Bt đối nhau
ài 1 a)như hình vẽ ta thấy góc A= góc B=90° => a//b( vì có 2 góc so le trong bằng nhau) b) vì a//b nên D1=E2=60°( hai góc đồng vị) Mà E1+E2=180°=> E1=180-60=130°

\(a)\hept{\begin{cases}\text{Ta có:}\widehat{A_4}=\widehat{B_2}=110^0\\\text{Mà chúng so le trong}\end{cases}}\)
\(\Rightarrow a//b\)
\(b)\hept{\begin{cases}\text{Ta có:}c\perp a\left(gt\right)\\\text{Mà }a//b\left(cmt\right)\end{cases}}\)
\(\Rightarrow c\perp b\)
\(c)\text{Ta có:}\widehat{B_1}+\widehat{B_2}=180^0\left(\text{kề bù}\right)\)
\(\Rightarrow\widehat{B_1}=180^0-\widehat{B_2}\)
\(\Rightarrow\widehat{B_1}=180^0-110^0=70^0\)
\(\text{Ta có:}\widehat{B_1}=\widehat{B_3}=70^0\left(\text{đối đỉnh}\right)\)
\(\text{Ta có:}\widehat{B_3}=\widehat{C_3}\left(\text{Đồng vị}\right)\)
\(\Rightarrow\widehat{B_3}=\widehat{C_3}=70^0\)
a) Ta có: {ˆA4=110∘ˆB2=110∘⇒ˆA4=ˆB2=110∘{A4^=110∘B2^=110∘⇒A4^=B2^=110∘.
Mà hai góc ờ vị trí so le trong ⇒⇒ a//ba//b.
b) Ta có: {c⊥aa//b⇒c⊥b{c⊥aa//b⇒c⊥b
c) Vì a//b⇒ˆA4+ˆB1=180

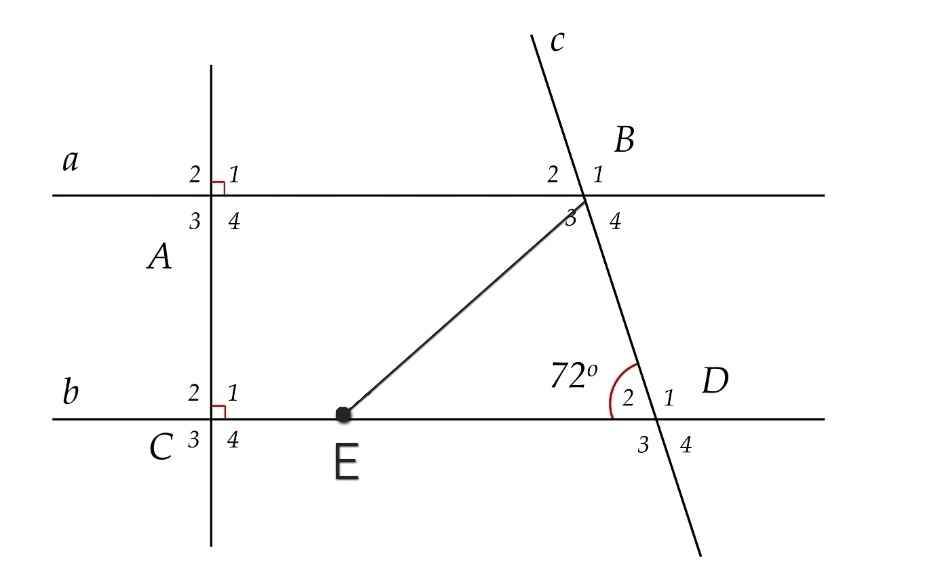 a) Ta có:
a) Ta có:
∠A₁ = ∠C₁ = 90⁰
Mà ∠A₁ và ∠C₁ là hai góc đồng vị
⇒ a // b
b) Ta có:
∠D₁ + ∠D₂ = 180⁰ (kề bù)
⇒ ∠D₁ = 180⁰ - ∠D₂
= 180⁰ - 72⁰
= 108⁰
Do a // b (cmt)
⇒ ∠ABD = ∠D₁ = 108⁰ (so le trong)
c) Do BE là tia phân giác của ∠ABD
⇒ ∠ABE = ∠ABD : 2
= 108⁰ : 2
= 54⁰




Kẻ tia CxCx là tia phân giác của ˆACDACD^ và DyDy là tia phân giác của ˆBDCBDC^, hai tia CxCx và DyDy cắt nhau tại EE.
ˆC1=ˆC2=60∘C1^=C2^=60∘ và ˆD1=ˆD2=30∘D1^=D2^=30∘
Kẻ tia Ez//m//nEz//m//n, tính ˆE1=60∘E1^=60∘ và
Đúng(2)
Kẻ tia CxCx là tia phân giác của \widehat{A C D}ACD và DyDy là tia phân giác của \widehat{B D C}BDC, hai tia CxCx và DyDy cắt nhau tại EE.
\widehat{C_1}=\widehat{C_2}=60^{\circ}C1=C2=60∘ và \widehat{D_1}=\widehat{D_2}=30^{\circ}D1=D2=30∘
Kẻ tia Ez / / m // nEz//m //n, tính \widehat{E_1}=60^{\circ}E1=60∘ và \widehat{E_2}=30^{\circ}E