Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

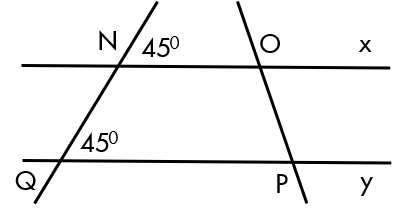
ta có góc QNO = 1800 - 450 = 1350
vì tổng 4 góc của một tứ giác bằng 3600
xét tứ giác QNOP
ta có góc NOP + góc QPO = 3600 - ( 450 + 1350) = 1800 (đpcm)

a/
\(Ax\perp m\left(gt\right);By\perp m\left(gt\right)\) => Ax//By (cùng vuông góc với m)
Mà Cz//Ax (gt)
=> Cz//By (cùng // với Ax)
b/
\(\widehat{BCz}=\widehat{ACB}-\widehat{C}=110^o-30^o=80^o\)
Ta có
Cz//By (cmt) \(\Rightarrow\widehat{BCz}=\widehat{CBy}=80^o\) (góc so le trong)
c/
\(CD\perp Ax\left(gt\right)\Rightarrow\widehat{ADC}=90^o\)
Cz//Ax (gt) \(\Rightarrow\widehat{A}=\widehat{C}=30^o\) (Góc so le trong)
Xét tg vuông ACD có
\(\widehat{ACD}=\widehat{ADC}-\widehat{A}=90^o-30^o=60^o\)

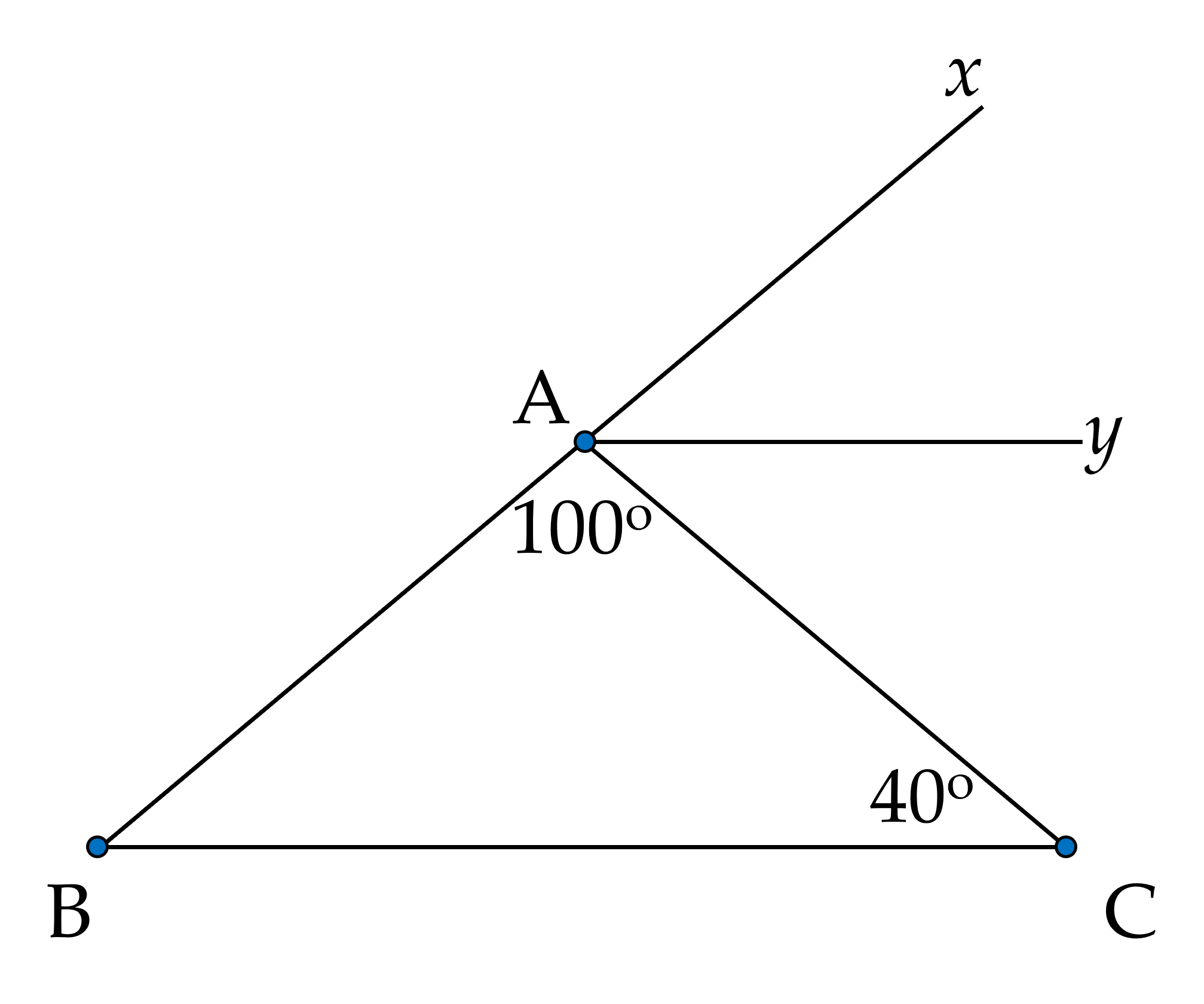
a) Ta có:
∠CAx + ∠CAB = 180⁰ (kề bù)
⇒ ∠CAx = 180⁰ - ∠CAB
= 180⁰ - 100⁰
= 80⁰
b) Do Ay là tia phân giác của ∠CAx
⇒ ∠CAy = ∠xAy = ∠CAx : 2
= 80⁰ : 2
= 40⁰
⇒ ∠CAy = ∠ACB = 40⁰
Mà ∠CAy và ∠ACB là hai góc so le trong
⇒ Ay // BC
c) Do Ay // BC
⇒ ∠ABC = ∠xAy = 40⁰ (đồng vị)

a/
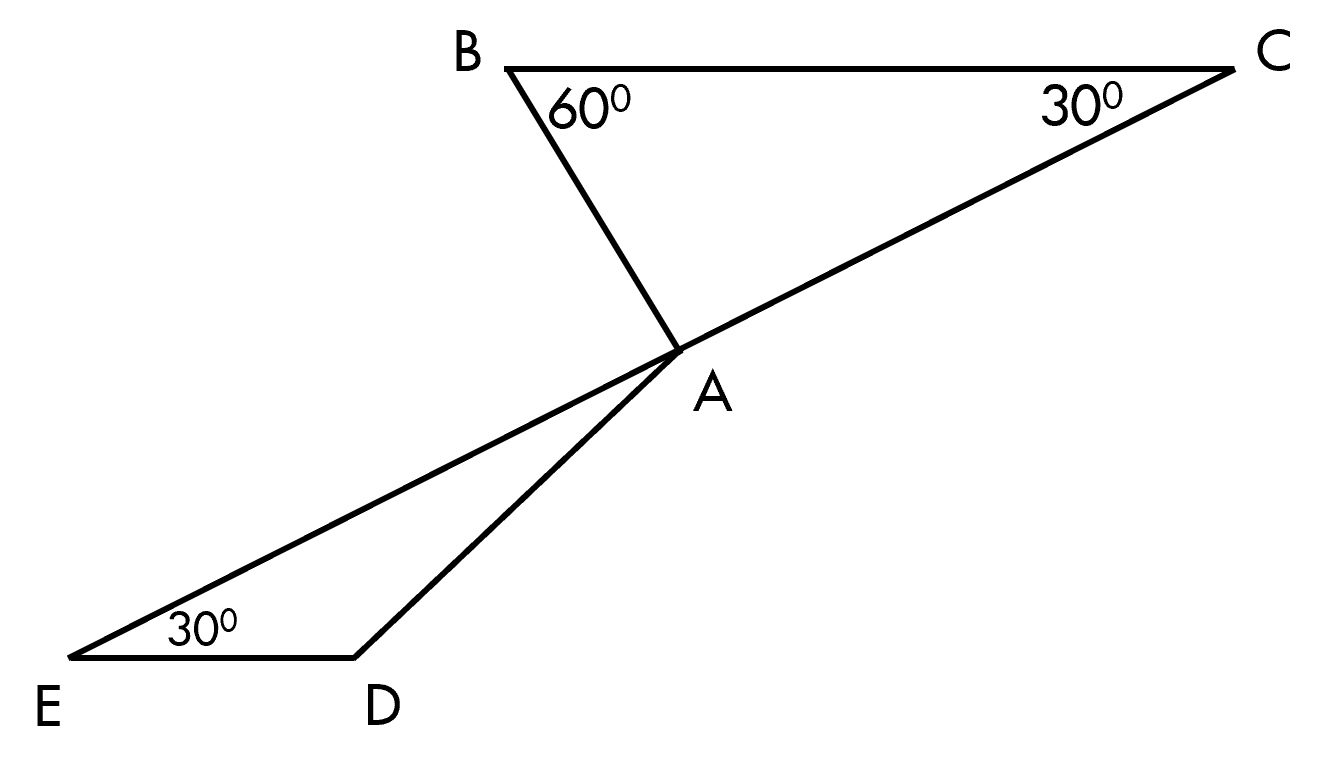
\(\widehat{BCE}=\widehat{CED}=30^o\)
Hai góc trên ở vị trí sole trong => BC//DE
b/
Ta có
BC//DE (cmt) \(\Rightarrow\widehat{AFB}=180^o-\widehat{EDF}\) (Hai góc trong cùng phía bù nhau)
\(\Rightarrow\widehat{AFB}=180^o-135^o=45^o\)

a) Vẽ hình
 b) Ta có:
b) Ta có:
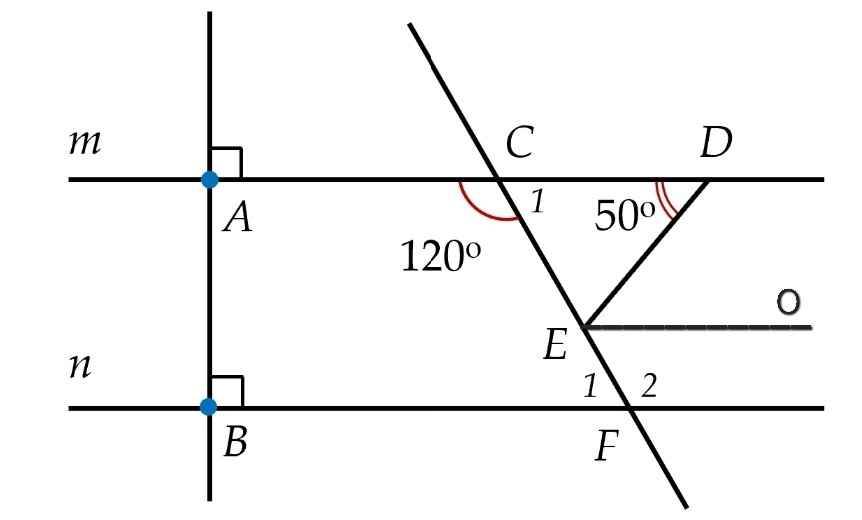
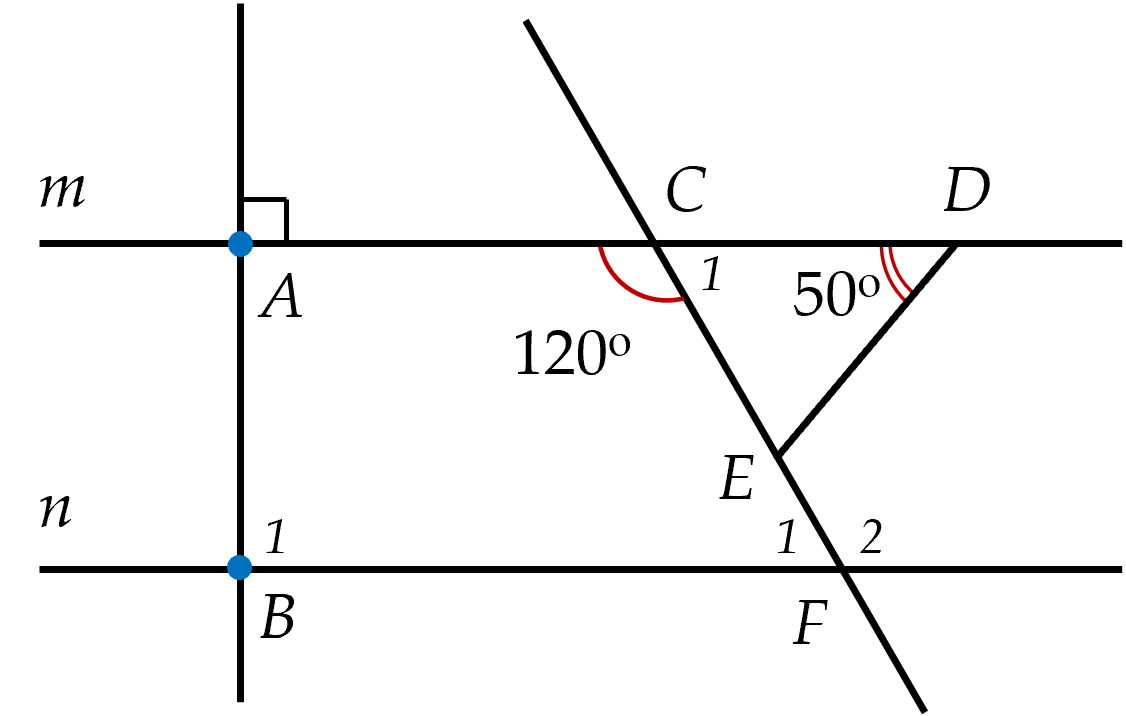
∠C₁ + ∠ACF = 180⁰ (kề bù)
⇒ ∠C₁ = 180⁰ - ∠ACF
= 180⁰ - 120⁰
= 60⁰
Do m // n (gt)
⇒ ∠F₁ = ∠C₁ = 60⁰ (so le trong)
c) Do AB ⊥ m (gt)
m // n (gt)
⇒ AB ⊥ n
d) Vẽ tia Eo // m // n như hình
Do Eo // m
⇒ ∠DEo = ∠ADE = 50⁰ (so le trong)
Do Eo // n
⇒ ∠FEo = ∠F = 60⁰ (so le trong)
⇒ ∠DEF = ∠DEo + ∠FEo
= 50⁰ + 60⁰
= 110⁰

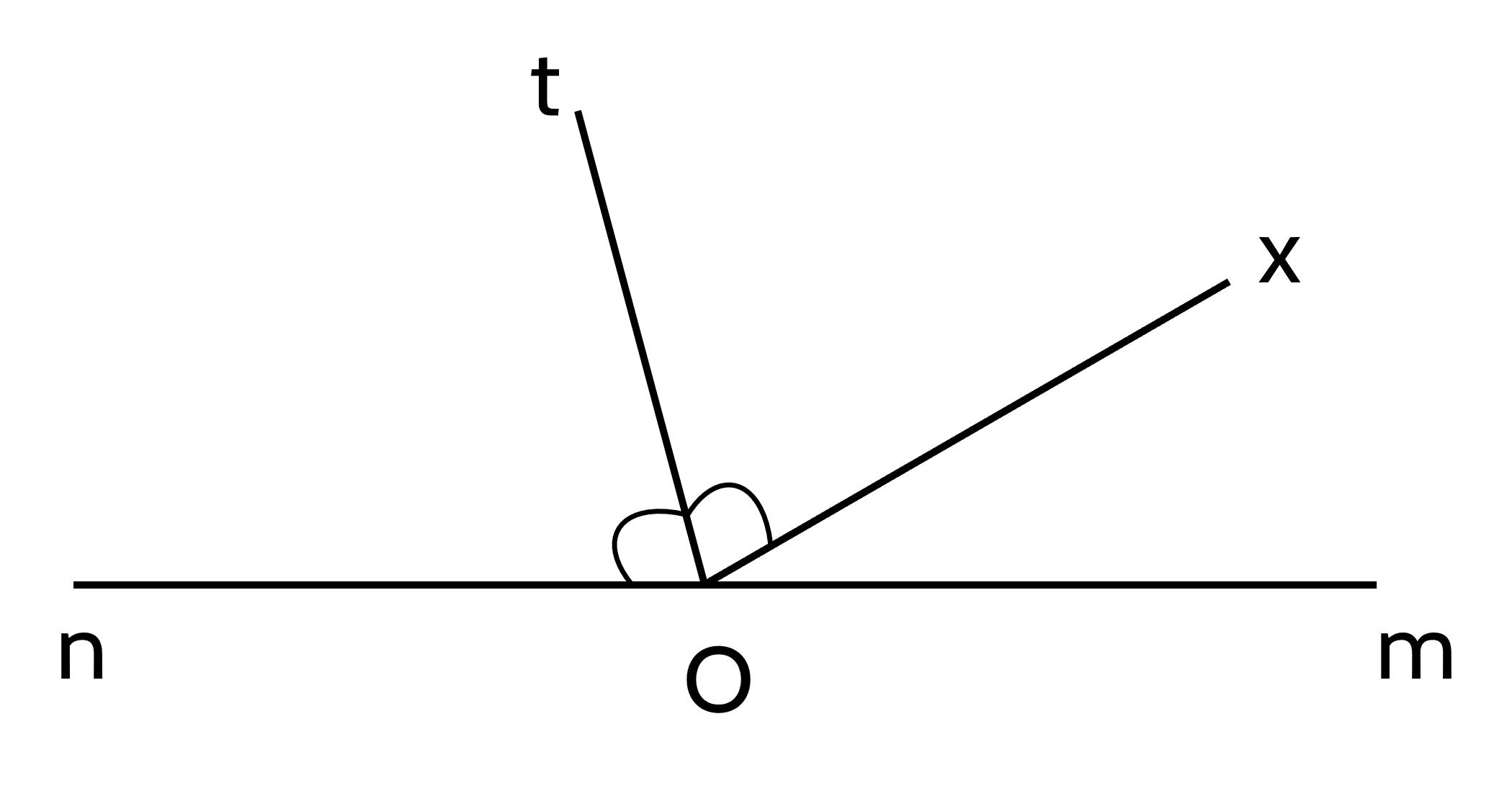
a) Ta có:
∠mOx + ∠nOx = 180⁰ (kề bù)
⇒ ∠nOx = 180⁰ - ∠mOx
= 180⁰ - 30⁰
= 150⁰
Do Ot là tia phân giác của ∠nOx
⇒ ∠nOt = ∠nOx : 2
= 150⁰ : 2
= 75⁰
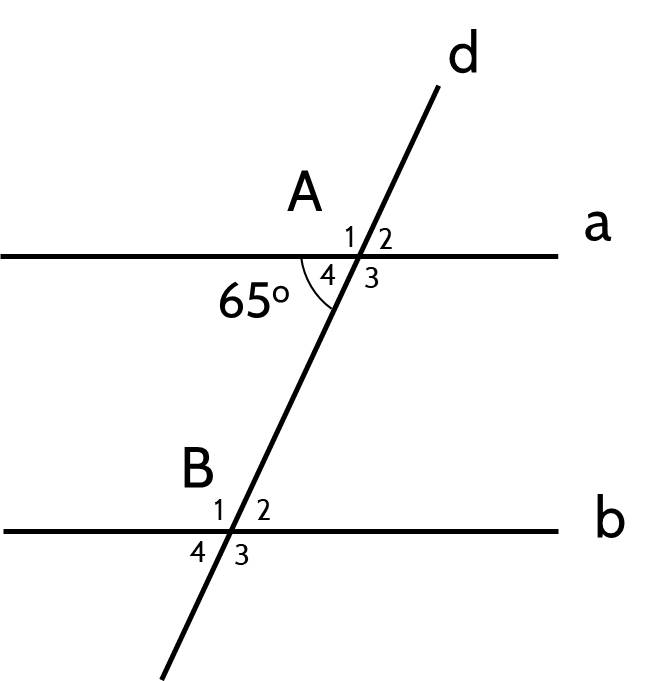
b) Do a // b
⇒ ∠B₄ = ∠A₄ = 65⁰ (đồng vị)
Ta có:
∠B₃ + ∠B₄ = 180⁰ (kề bù)
⇒ ∠B₃ = 180⁰ - ∠B₄
= 180⁰ - 65⁰
= 115⁰
Tính số đo góc �3^B3.
Hướng dẫn giải:a) ���^+���^=180∘mOx+xOn=180∘
Vậy ���^=180∘−30∘=150∘nOx=180∘−30∘=150∘.
��Ot là tia phân giác của ���^nOx, suy ra ���^=12.���^=75∘nOt=21.nOx=75∘.
b) a // b suy ra �4^=�2^=65∘A4=B2=65

 a) Ta có:
a) Ta có:
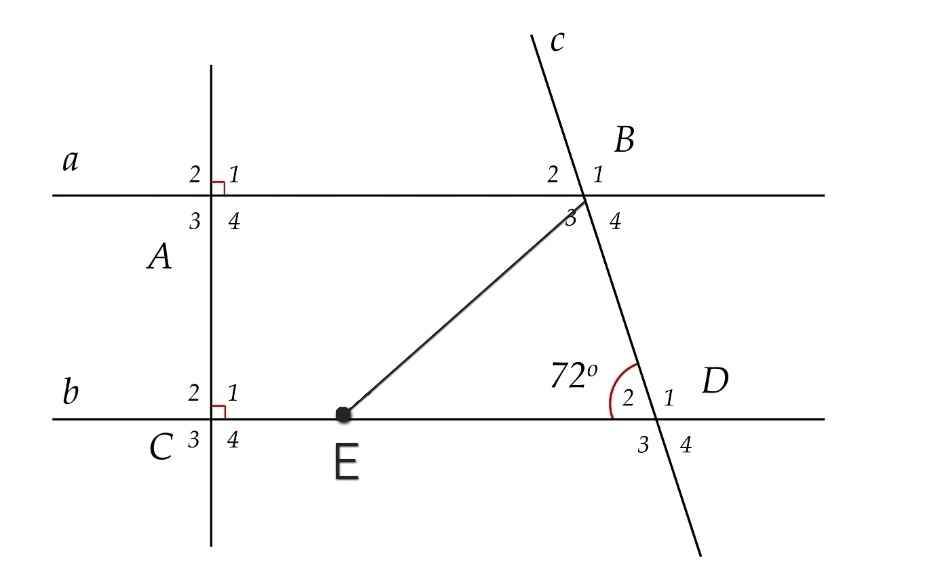
∠A₁ = ∠C₁ = 90⁰
Mà ∠A₁ và ∠C₁ là hai góc đồng vị
⇒ a // b
b) Ta có:
∠D₁ + ∠D₂ = 180⁰ (kề bù)
⇒ ∠D₁ = 180⁰ - ∠D₂
= 180⁰ - 72⁰
= 108⁰
Do a // b (cmt)
⇒ ∠ABD = ∠D₁ = 108⁰ (so le trong)
c) Do BE là tia phân giác của ∠ABD
⇒ ∠ABE = ∠ABD : 2
= 108⁰ : 2
= 54⁰

a: góc O1=góc O2=140/2=70 độ
góc O3=góc O4=180-70=110 độ
b: góc O1+góc O3=360/2=180 độ
góc O2+góc O4=180 độ
Góc O1 và O3 là hai góc kề bù rồi nên mặc nhiên tổng của hai góc đó bằng 180 độ nha bạn
Tương tự với cặp góc O2 và O4
=>Không tính được
c: góc O2=góc O1
nên góc O2-góc O1=10 độ là sai đề rồi bạn

a, các cặp góc đối đỉnh là :
\(\widehat{O_1}\) và \(\widehat{O_3}\)
\(\widehat{O_2}\) và \(\widehat{O_4}\)
b, Ta có : \(\widehat{O_1}+\widehat{O_3}=110^0\)
Mà \(\widehat{O_1}\) đối đỉnh với \(\widehat{O_2}\)
\(\Rightarrow\widehat{O_1}=\widehat{O_3}=\dfrac{110^0}{2}=55^0\)
\(\Rightarrow\widehat{O_1}+\widehat{O_2}=180^0\)
\(\Rightarrow\widehat{O_2}=180^0-55^0=125^0\)
Mà \(\widehat{O_2}\) đối đỉnh với \(\widehat{O_4}\)
\(\Rightarrow\widehat{O_2}=\widehat{O_4}=125^0\)



Suy ra \widehat{O_1} = \widehat{O_2} + 70^{\circ}O1= O2+70∘
Mà \widehat{O_1}O1 và \widehat{O_2}O2 là hai góc kề bù nên \widehat{O_1} + \widehat{O_2} = 180^{\circ}O1+ O2=180∘.
Thay \widehat{O_1} = \widehat{O_2} + 70^{\circ}