Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số bé là a, số lớn là b
Theo bài ra ta có:
a: b= 2: 5
=> a/2 = b/5
Đặt a/2= b/5 = k
=> a= 2k , b=5k
=> a . b = 2k .5 k = 10 . k^2 mà a .b = 40
=> 10 . k^2 = 40 => k^2= 4
=> k= 2 hoặc -2
TH: k = 2 => a = 2 x 2 = 4 ; b = 2 x 5 = 10
TH : k = -2 => a= -2 x 2= -4 ; b = -2 x 5 = -10
Vậy hai số đó là 4 và 10 hoặc -4 và -10
đúng nhé
Gọi 2 số đó là a và b (a>b; b khác 0) ta có:
\(a:b=\frac{2}{5}\) và \(a\times b=40\)
=> \(a:b\times a\times b=\frac{2}{5}\times40\)
\(a\times a=16\)
-> \(a=4\) hoặc \(a=-4\)
+ Nếu a=4 thì \(4:b=\frac{2}{5}\)
\(b=4:\frac{2}{5}\)
\(b=10\)
+ Nếu a= -4 thì \(-4:b=\frac{2}{5}\)
\(b=-4:\frac{2}{5}\)
\(b=-10\)
Vậy có hai cặp số là a=4 và b = 10 ; a= -4 và b = -10

Ý nghĩa gcvh và các bác nhé ạ chưa được phân phối các sản sapa và cắt tóc nam nữ tính ibffggy đâu ạ

ba=52 nên a = 2k , b = 5k (k\inℤ,k\ne0)(k∈Z,k̸=0)
Từ a . b = 40 \Rightarrow2k\cdot5k=40⇒2k⋅5k=40
\Rightarrow k^2=40:(2\cdot5)⇒k2=40:(2⋅5)
\Rightarrow k^2=40:10⇒k2=40:10
\Rightarrow k^2=4\Rightarrow k=\pm2⇒k2=4⇒k=±2
Vậy : a = 4 b = 10 (k=2)(k=2)
a = -4 b = -10 (k=-2)(k=−2)
\(\frac{a}{b}=\frac{2}{5}\) nên a = 2k , b = 5k \((k\inℤ,k\ne0)\)
Từ a . b = 40 \(\Rightarrow2k\cdot5k=40\)
\(\Rightarrow k^2=40:(2\cdot5)\)
\(\Rightarrow k^2=40:10\)
\(\Rightarrow k^2=4\Rightarrow k=\pm2\)
Vậy : a = 4 b = 10 \((k=2)\)
a = -4 b = -10 \((k=-2)\)

Cho phân số \(\dfrac{a}{b}=\dfrac{2}{5}\) \(\rightarrow\) \(a=2k\) \(,\) \(b=5k\) \(\left(k\in Z,k\ne0\right)\)
Từ \(a.b=40\) \(\Rightarrow\) \(2k.5k=40\) \(\Rightarrow\) \(k^2=4\Rightarrow k=\pm2\)
Vậy \(a=4\) \(,\) \(b=10\) \(\left(k=2\right)\) và \(a=-4\) \(,\) \(b=-10\) \(\left(k=-2\right)\)
Gọi hai số cần tìm là m và n. Ta có: 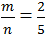
Vì
Suy ra:
Vì n2 = 100 nên n = 10 hoặc n = -10
Nếu n = 10 thì m = 2/5. 10 = 4
Nếu n = -10 thì m = 2/5. (-10) = 4
Vậy hai số cần tìm là m = 4 , n = 10 hoặc m = -4 , n = -10
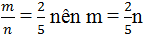
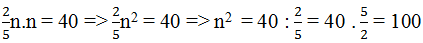
nếu số đó là 5 và 10 thì ps đó là :
\(\frac{5}{10}=\frac{1}{2}\)
4 và 10