Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-hình bạn tự ve
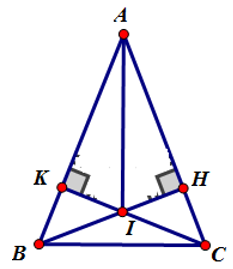
a) CM : AH = AK
xét tam giác kbc và tam giác hcb có:
góc b = góc c(ll)
bc: cahj chung
góc hbc= góc hcb
=> hai tam giác trên = nhau
mà tam giác abc cân tại a
=> ab=ac
mà kb=hc (tương ứng)
=> ak = ah( ak= ab- kb, ah= ac-hc)
thôi làm luôn câu b
nối a và i thành đg thẳng ta sẽ có 2 tam giác aki và ahi
xét tam giác aki và ahi ta có
ak= ah (câu a)
goác aki = góc ahi( đều 90 độ=> ll ở câu a)
ki = hi ( ll ở câu a
=> hai tam giác trên = nhau
mà 2 tam giác bằng nhau thì 2 góc tg ứng = nhau => góc kai= hai
=> ai là tia phan giac cua goc a
máy cái tam giác mk ko ghi in hoa đâu đó nha

K B A C H I M x y
a) Xét \(\Delta ABH\)và\(\Delta ACK\)có:
\(\widehat{A}\)chung
\(AB=AC\)(\(\Delta ABC\)cân)
\(\widehat{K}=\widehat{H}=90^o\)
\(\Rightarrow\Delta ABH=\Delta ACK\left(g.c.g\right)\)
\(\Rightarrow AH=AK\)(2 cạnh tương ứng)
\(\Leftrightarrow\widehat{ABH}=\widehat{ACK}\)(2 góc tương ứng)
\(\Leftrightarrow BH=CK\)(2 cạnh tương ứng)
\(\Leftrightarrow KB=HC\)(2 cạnh tương ứng)
b) Xét \(\Delta AIB\)và\(\Delta AIC\)có:
\(AB=AC\)(\(\Delta ABC\)cân)
\(\widehat{ABH}=\widehat{ACK}\left(cmt\right)\)
\(AH=CK\left(cmt\right)\)
\(\Rightarrow\Delta AIB=\Delta AIC\left(c.g.c\right)\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\)(2 góc tương ứng)
c) Bạn tự làm nha.
d) Vì \(Cx\perp AC\)và \(By\perp AB\)\(\Rightarrow\widehat{ABM}=\widehat{ACM}=90^o\)
mà \(\Delta ABC\)cân nên \(\widehat{ABC}=\widehat{ACB}=x\left(x< 90^o\right)\)
Ta có: \(\widehat{ABM}-\widehat{ABC}=\widehat{ACM}-\widehat{ACB}=90^o-x=\widehat{CBM}=\widehat{BCM}\)
Do \(\widehat{CBM}=\widehat{BCM}\Rightarrow\Delta MBC\)cân tại M
Xét \(\Delta BKI\)và \(\Delta CHI\)có:
\(\widehat{BKC}=\widehat{CHB}=90^o\)
\(BK=CH\)(theo a)
\(\widehat{ABH}=\widehat{ACK}\)(theo a)
\(\Rightarrow\Delta BKI=CHI\left(g.c.g\right)\)
\(\Leftrightarrow IB=IC\)(2 cạnh tương ứng)
Vì \(\Delta BIC\)có \(IB=IC\) nên \(\Delta BIC\)là tam giác cân tại I

a) Xét ΔABH vuông tại H và ΔACK vuông tại K có:
AB = AC (Do ΔABC cân tại A)
góc A chung
Nên ΔABH = ΔACK (cạnh huyền – góc nhọn) ⇒ AH = AK (hai cạnh tương ứng).
b) Xét ΔAIK vuông tại K và ΔAIH vuông tại H có:
AH = AK (theo phần a)
AI chung
⇒ ΔAIK = ΔAIH (cạnh huyền – cạnh góc vuông).
⇒ góc IAK = góc IAH (hai góc tương ứng)
Vậy AI là tia phân giác của góc A.