Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x z y O
gọi đường vuông góc với Oy mà MP.
gọi đường vuông góc với Ox là MQ.
xét tam giác OMP và tam giác OMQ, ta có: OM chung.
\(\widehat{MPO}=\widehat{MQO}=90^o\)
\(\widehat{POM}=\widehat{QOM}\)(tia phân giác của Oz).
=> tam giác OMP = QMQ (ch-gn)
=> MP = MQ (cạnh tương ứng)
mà MP = 5 cm
=> MQ = 50 cm
=> khoảng cách từ M -> Ox là 5cm
vì khoảng cách từ M -> Ox là 5 cm nên khoảng cách từ M -> Ox là 5 cm (tính chất của tia phân giác).

Vì M thuộc Oz là tia phân giác của góc x O y ^ nên M cách đều hai tia Ox và Oy
Vậy khoảng cách từ M đến Ox bằng khoảng cách từ M đến Oy và bằng 5 cm.
Chọn đáp án B

Gọi Đường vuông góc với Oy là MP
Gọi đường vuông góc với Ox là MQ
Xét tam giác OMP và tam giác OMQ có:
OM chung
Góc MPO=MQO=900
POM=QOM( Phân giác Oz)
=> Tam giác OMP=tam giác OMQ(ch-gn)
=> MP=MQ(cạnh tương ứng)
Mà MP=5 cm
=> MQ=50
Vậy khoảng cách từ M đến Ox là 5 cm

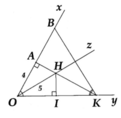
Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.
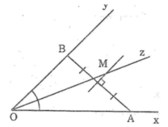

Có Oz là tia phân giác của \(\widehat{xOy}\)
Nên khoảng cách từ điểm M sẽ cách đều 2 cạnh ( Đlý)
mà khoảng cách từ M đến Oy là 5cm
Suy ra khoảng cách từ điểm M đến Ox là 5cm