Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để phương trình có một trong các nghiệm là x=2 nên
Thay x=2 vào phương trình, ta được:
\(\left(m+2\right)^2-\left(2-3m\right)^2=0\)
\(\Leftrightarrow\left(m+2+2-3m\right)\left(m+2-2+3m\right)=0\)
\(\Leftrightarrow4m\cdot\left(-2m+4\right)=0\)
mà 4>0
nên m(-2m+4)=0
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\-2m+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\-2m=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)
Vậy: Để phương trình có 1 trong các nghiệm là x=2 thì \(m\in\left\{0;2\right\}\)
`x=2` là nghiệm phương trình nên thay x=2 vào ta có:
`(2+m)^2-(2-3m)^2=0`
`=>(2+m-2+3m)(2+m+2-3m)=0`
`=>4m(4-2m)=0`
`=>m(2-m)=0`
`=>` \left[ \begin{array}{l}m=0\\m=1\end{array} \right.

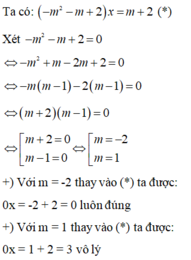
Vậy với m = -2 thì phương trình đã cho có vô số nghiệm.
Đáp án cần chọn là: C

a: Để đây là phương trình bậc nhất một ẩn thì 3m-2<>0
=>m<>2/3
b: x=-2 là nghiệm của phương trình
=>-2(3m-2)+5=m
=>-6m+4+5-m=0
=>9-7m=0
=>m=9/7

\(\left(3m-2\right)x+5=m\)
\(\Leftrightarrow\left(3m-2\right)x+5=0\)
Để PT trên là bậc nhất một ẩn thì :
\(3m-2\text{≠}0\) \(\Leftrightarrow3m\text{≠}2\Leftrightarrow m\text{≠}\dfrac{2}{3}\)
b) \(\left(3m-2\right)x+5=m\)
\(\Leftrightarrow\left(3m-2\right)\cdot2+5=m\)
\(\Leftrightarrow6m-4+5=m\)
\(\Leftrightarrow5m=-1\)
\(\Leftrightarrow m=\left(-1\right)\div5\)
\(\Leftrightarrow m=-\dfrac{1}{5}\)
Vậy \(m=-\dfrac{1}{5}\) thì phương trình nhận \(x=2\) nghiệm
theo đề ta có
(m2-m)x=m2 +3m+2x+1
lại có : m2 +3m+1=\(m+2m\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{5}{4}\\ \left(m+\dfrac{3}{2}\right)^2-\dfrac{5}{4}#0\)
nên m2 +3m+2x+1#0
để pt vô nghiệm thì (m2-m)x=0
suy ra : (m2-m)x=2x
=> m2-m-2=0
<=> (m-2)(m+1)=0
<=> m=2; hoặc m=-1 thì pt vô nghiệm
(có gì sai xin mọi người sửa giùm cho !!!)
\(m^2+3m+1=m^2+2m\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{5}{4}\\ =\left(m+\dfrac{3}{2}\right)^2-\dfrac{5}{4}\)
nên m2 +3m+1#0(ở dưới mình đánh máy bị sai thứ lỗi nha)