Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

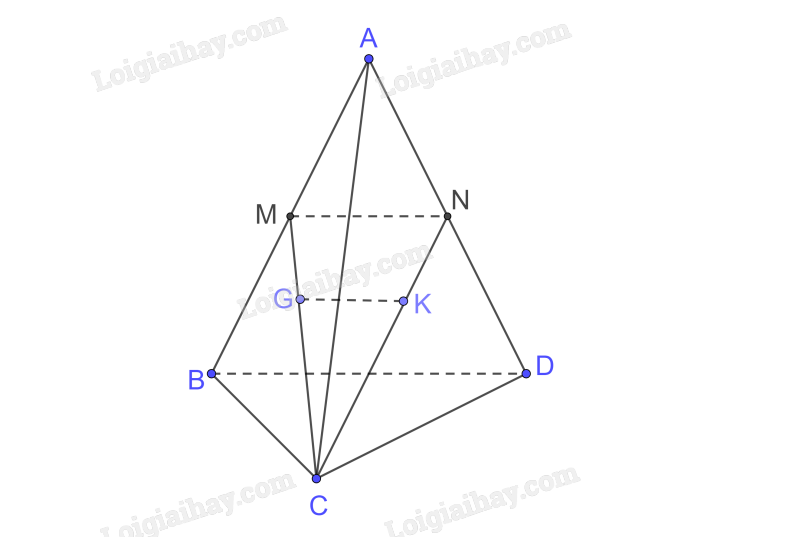
a) Xét tam giác ABD có
M, N tương ứng là trung điểm của AB, AD
\( \Rightarrow \) MN là đường trung bình của tam giác ABD
\( \Rightarrow \) MN // BD mà BD \( \bot \) BC (\(\widehat {CBD} = {90^0}\))
\( \Rightarrow \) MN \( \bot \) BC.
b) Vì G, K tương ứng là trọng tâm của các tam giác ABC, ACD nên \(\frac{{CG}}{{CM}} = \frac{{CK}}{{CN}} = \frac{2}{3}\)
\( \Rightarrow \) GK // MN (Định lý Talet) mà MN \( \bot \) BC
\( \Rightarrow \) GK \( \bot \) BC.

a: SO vuông góc (ABC)
=>(SGO) vuông góc (ABC)
b: ((SAB);(ABC))=(SG;AG)=góc SGA
\(AG=\dfrac{a\sqrt{3}}{3}\)
cos SGA=AG/SA=căn 3/3:2=căn 3/6
=>góc SGA=73 độ

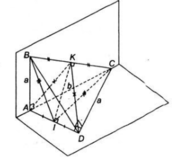


Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.

a: ABCD.A'B'C'D là hình lập phương
=>BB'C'C là hình vuông
=>BB'\(\perp\)BC
b: ABCD.A'B'C'D là hình lập phương
=>ABB'A' là hình vuông
=>BB'\(\perp\)AB
c: Ta có: ABCD.A'B'C'D' là hình lập phương
=>A'B'C'D' là hình vuông
=>A'D'//B'C'
mà B'C'\(\perp\)BB'(BCC'B' là hình vuông)
nên BB'\(\perp\)A'D'

a: ABCD.A'B'C'D' là hình lập phương
=>ABCD là hình vuông
=>AB\(\perp\)BC
b: Ta có: A'B'\(\perp\)B'C'(A'B'C'D' là hình vuông)
A'B'\(\perp\)BB'(A'B'BA là hình vuông)
B'C',BB' cùng thuộc mp(BCB')
Do đó: A'B'\(\perp\)(BCB')
=>A'B'\(\perp\)BC
