Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
tìm p/s tối giản biết tích của tử và mẫu = 220 . p/s tối giản đó có thể biểu diễn bởi 1 số thập phân

tìm p/s tối giản biết tích của tử và mẫu = 220 . p/s tối giản đó có thể biểu diễn bởi 1 số thập phân

tìm p/s tối giản biết tích của tử và mẫu = 220 . p/s tối giản đó có thể biểu diễn bởi 1 số thập phân

tìm p/s tối giản biết tích của tử và mẫu = 220 . p/s tối giản đó có thể biểu diễn bởi 1 số thập phân

Ta có phân số AB trên BA(xin lỗi vì tui ko viết đc phân số,nên phân số)
Ta tách 2 phân số: AB và BA
AB x BA=220
(Ax10+B) x (Bx10+A)=220
(A x10-A) x (Bx10-B)=220
Ax11 x Bx11=220
ABx11=220
AB =220:11
AB =20
=> BA= 11 vì 11x20=220(hoặc 220:20=11)
Vậy P/s đó là 11 trên 20
Ta có thể chia nó thành số thập phân dưới dạng:11:20=0,55
Đs:11 trên 20
Nhớ tích tôi nhé bạn,nếu chưa hiểu thì hỏi tui nhé
Chúc cậu học tốt ^_^
Ta có phân số AB trên BA(xin lỗi vì tui ko viết đc phân số,nên phân số)
Ta tách 2 phân số: AB và BA
AB x BA=220
(Ax10+B) x (Bx10+A)=220
(A x10-A) x (Bx10-B)=220
Ax11 x Bx11=220
ABx11=220
AB =220:11
AB =20
=> BA= 11 vì 11x20=220(hoặc 220:20=11)
Vậy P/s đó là 11 trên 20
Ta có thể chia nó thành số thập phân dưới dạng:11:20=0,55
Đs:11 trên 20
Nhớ tích tôi nhé bạn,nếu chưa hiểu thì hỏi tui nhé
Chúc cậu học tốt ^_^

220 = 4. 5. 11 nên ta có các phân số tối giản sau đây thỏa mãn các điều kiện của bài toán:
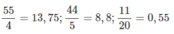

220= \(2^2\).5.11 nên ta có các phân số tối giản sau đây thỏa mãn các điều kiện của bài toán:
\(\dfrac{55}{4}=13,75;\dfrac{44}{5}=8,8;\dfrac{11}{20}=0,55\)
220 = 22. 5. 11 nên ta có các phân số tối giản sau đây thỏa mãn các điều kiện của bài toán:

Để chứng minh \(\frac{n+2011}{n+2012}\) là phân số tối giản => ( n+2011; n+2012 ) = 1
Gọi d là \(ƯCLN\left(n+2011;n+2012\right)\)
\(\Rightarrow\hept{\begin{cases}n+2011⋮d\\n+2012⋮d\end{cases}\Rightarrow\left(n+2012\right)-\left(n+2011\right)⋮d}\)
\(\Rightarrow1⋮d\Rightarrow d=1\)
\(\Rightarrow\frac{n+2011}{n+2012}\) là phân số tối giản.
gọi d là UCLN(n+2011,n+2012)
\(\Rightarrow\orbr{\begin{cases}n+2011⋮\\n+2012⋮\end{cases}}d\)
\(\Rightarrow\left(n+2012\right)-\left(n+2011\right)⋮d\)
\(\Rightarrow n+2012-n-2011⋮d\)
\(\Rightarrow1⋮d\Rightarrow d\inƯCLN\left(1\right)=\left\{\pm1\right\}\)
=> UCLN(N+2011,2012) = 1
=>\(\frac{2011}{2012}\)Là phân số tối giản
Chúc bạn học tốt !
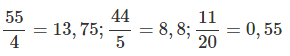
xin lỗi mik tưởng là 120 ...xl bn nhìu