Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án A
Phương pháp: Cường độ dòng điện hiệu dụng I = U/Z
Đoạn mạch gồm RLC mắc nối tiếp : 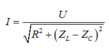 (1)
(1)
Khi nối tắt tụ : 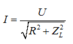
Từ (1) và (2)
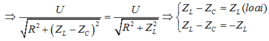
![]()

Câu 1:
R thay đổi để PR max thì: \(R=\sqrt{r^2+(Z_L-Z_C)^2}=Z_{NB}\)
\(\Rightarrow U_R=U_{NB}=80\sqrt 3\) (V) (1)
\(U^2=(U_R+U_r)^2+(U_L-U_C)^2=240^2\) (2)
Và: \(U_{NB}^2=U_r^2+(U_L-U_C)^2=3.80^2\) (3)
Lấy (2) - (3) vế với vế ta có: \((U_R+2U_r).U_R=6.80^2\Rightarrow U_r=40\sqrt 3\)
Vậy hệ số công suất: \(\cos\varphi=\dfrac{U_r+U_R}{U}=\dfrac{\sqrt 3}{2}\)

Đáp án C
Do dòng điện trong mạch sớm pha 450 so với điện áp hai đầu đoạn mạch nên ta có độ lệch pha giữa u và i là φ = -π/4 rad.
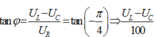
![]()
![]()
![]()

\(Z_L=\omega L=100\sqrt{3}\Omega\)
C thay đổi để Uc max khi: \(Z_C=\frac{R^2+Z_L^2}{Z_L}=\frac{100^2+3.100^2}{100\sqrt{3}}=\frac{4}{\sqrt{3}}.100\Omega\)
\(U_{cmax}=U\frac{\sqrt{R^2+Z_L^2}}{R}=100\frac{\sqrt{100^2+3.100^2}}{100}=200V\)

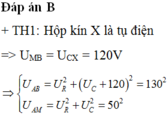
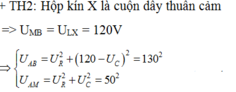
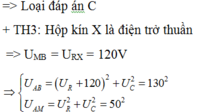
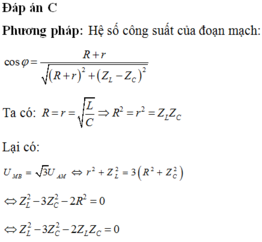

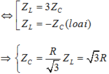
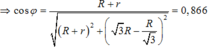
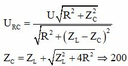
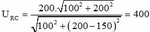
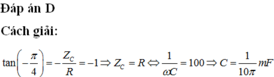
U U X R U α
Dùng định lý trong tam giác \(\cos \alpha = \frac{U_R^2+U^2 - U_X^2}{2U_RU} = \frac{0,8^2+1^2-0,5^2}{2.0,8} = 0,8687.\)
Chọn đáp án A.0,87