Gọi trọng tâm của tam giác ABC là G

Vì G là trọng tâm tam giác ABC 

\(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)

+) Xét \(\overrightarrow{\text{AA}'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\overrightarrow{0}\)

\(\Leftrightarrow\overrightarrow{AG}+\overrightarrow{GA'}+\overrightarrow{BG}+\overrightarrow{GB'}+\overrightarrow{CG}+\overrightarrow{GC'}=\overrightarrow{0}\)

\(\Leftrightarrow\left(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}\right)+\left(\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}\right)=\overrightarrow{0}\)

\(\Leftrightarrow\left(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}\right)-\overrightarrow{0}=\overrightarrow{0}\)

=> G đồng thời là trọng tâm của tam giác A'B'C'

Tổng số bạn đăng kí clb Tiếng Anh hoặc clb Nhạc hoặc cả `2` clb là:

              `16+19-9=26` (bạn)

Vậy còn lại số bạn không đăng kí câu lạc bộ nào là:

              `40-26=14` (bạn)

16

\(48=2^4.3\\ 36=2^2.3^2\\ \RightarrowƯCLN_{\left(48;36\right)}=2^2.3=12\\ \Rightarrow A\cap B=ƯC_{\left(48;36\right)}=Ư_{\left(12\right)}=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)

`A={1;2;3;4;6;8;12;16;24;48}`

`B={1;2;3;4;6;9;12;18;36}`

 `=>A nn B={1;2;3;4;6;12}`

Tổng quãng đường đi được thì có lẽ là : 8 + 3 + 4 = 15km

Nhưng độ lớn dịch chuyển thì đơn giản chỉ là 4 km. Để làm được chúng ta cần vẽ ra giấy hoặc có thể tưởng tượng nhưng mà phải biết các hướng đông tây nam bắc. Khi biết rồi thì rất dễ. Chúc học tốt !!

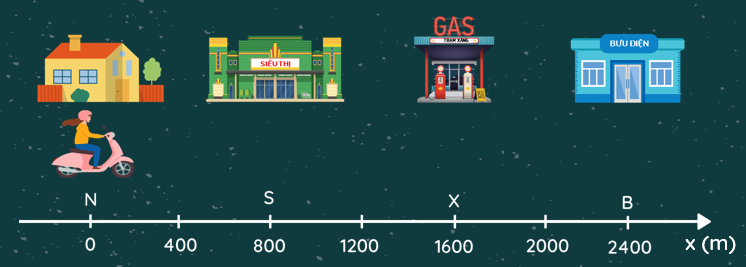
quãng đường người đó đã đi:

S = NS+NB = 800+2400 =3200m=3.2km

độ dời của người đó bằng khoảng cách từ vị trí ban đầu đến bưu điện bằng NB = 2400m = 2.4km

Quãng đường người đó đã đi được là: \(NS+SX+XN+NB=800+\left(1600-800\right)+1600+2400=5600\left(km\right)\)

Độ dời của người đó là: \(NS+SX-XN+NB=800+\left(1600-800\right)-1600+2400=2400\left(km\right)\)

Chọn vật 3 là đất, vật 2 là ô tô A, vật 1 là ô tô B.

Áp dụng công thức cộng vận tốc, vận tốc của B so với A là:

Do hai xe chạy cùng chiều, nên chiếu các vecto vận tốc lên phương chuyển động.

v12 = v13 – v23 = 60 – 45 = 15 km/h.

Vận tốc của A so với B là: v21 = v23 – v31 = 45 – 60 = - 15 km/h.

15

\(-5\left(x+4\right)+2\left(y+1\right)=-5x+2y-18\)

Hay đó mà giỏi