Gọi vận tốc bè gỗ là v₁ (km/h) (v₁ > 0)

=> Vận tốc thuyền : v₁ + 4 km/h (v₁ + 4 > 0)

Đổi : 3 giờ 20 phút = 10/3 giờ

Ta có v₁.10/3 + v₁.\(\frac{10}{v_1+4}\) = (v₁ + 4).\(\frac{10}{v_1+4}\) (= 10)

=> v₁.10/3 + v₁.\(\frac{10}{v_1+4}\) = v₁.\(\frac{10}{v_1+4}\)+ 4\(\frac{10}{v_1+4}\)

=> \(\frac{v_1.10}{3}=\frac{40}{v_1+4}\)

=> 3.40 = (v₁+ 4).v₁.10

=> (v₁ + 4).v₁ = 12

=> (v₁)² + 4.v₁ - 12 = 0

=> (v₁ + 2)(v₁ - 6) = 0

=> \(\orbr{\begin{cases}v_1+2=0\\v_1-6=0\end{cases}}\Rightarrow\orbr{\begin{cases}v_1=-2\left(\text{loại}\right)\\v_1=6\left(tm\right)\end{cases}}\)

Vậy vận tốc của bè là 6km/h

+) Áp dụng bất đẳng thức Cauchy-Schwarz, ta được: \(A=\sqrt{7-x}+\sqrt{2+x}\le\sqrt{2\left(7-x+2+x\right)}=3\sqrt{2}\)

Đẳng thức xảy ra khi \(7-x=2+x\Leftrightarrow x=\frac{5}{2}\)

+) \(A=\sqrt{7-x}+\sqrt{2+x}\Rightarrow A^2=9+2\sqrt{\left(7-x\right)\left(2+x\right)}\ge9\Rightarrow A\ge3\)

Đẳng thức xảy ra khi \(\left(7-x\right)\left(2+x\right)=0\Leftrightarrow\orbr{\begin{cases}x=7\\x=-2\end{cases}}\)

Vậy \(MinA=3\Leftrightarrow x\in\left\{7;-2\right\};MaxA=3\sqrt{2}\Leftrightarrow x=\frac{5}{2}\)

bài 1 ta có 

\(\left(\frac{1}{a}+\frac{1}{b}\right)\left(2020a+2021b\right)\ge\left(\sqrt{2020}+\sqrt{2021}\right)^2\)  ( BDT Bunhia )

do đó

\(a+b=ab.\left(\frac{1}{a}+\frac{1}{b}\right)\ge\left(\frac{1}{a}+\frac{1}{b}\right)\left(2020a+2021b\right)\ge\left(\sqrt{2020}+\sqrt{2021}\right)^2\)

vậy ta có đpcm.

bài 2.

ta có \(VT=\sqrt{x-3}+\sqrt{5-x}\le2\)( BDT Bunhia )

\(VP=y^2+2.\sqrt{2019}y+2021=\left(y+\sqrt{2019}\right)^2+2\ge2\)

suy ra PT có nghiệm \(\hept{\begin{cases}x-3=5-x\\y+\sqrt{2019}=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=4\\y=-\sqrt{2019}\end{cases}}}\)

Bạn tham khảo câu hỏi tương tự ở link: https://olm.vn/hoi-dap/detail/332134284249.html 

Mình đã trả lời trong đó rồi đó ạ. 

1. Kkksmmxkidmfnjf is the only one ☝️ can have the same name for the only one ☝️ in his life that I am going on a different time for a few days to see him and he has a little time in my mind and the ^{_{rest up ⬆️ and the rest of the family I love 💗 to see the kids iriiriiriiiiio}}
2. ^{_{iiiiirioeookdmdmfj and I am going to go}} 

Phương trình tọa độ giao điểm giữa \(\left(d\right)\)và \(\left(P\right)\)là: 

\(x^2=mx-m+1\)

\(\Leftrightarrow x^2-mx+m-1=0\)(*)

Để \(\left(d\right)\)và \(\left(P\right)\)cắt nhau tại hai điểm phân biệt thì (*) có hai nghiệm phân biệt \(x_1,x_2\).

\(\Delta=m^2-4\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2>0\Leftrightarrow m\ne2\).

Theo định lí Viete: \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}}\).

\(P=\frac{2x_1x_2+3}{x_1^2+x_2^2+2\left(x_1x_2+1\right)}=\frac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=\frac{2\left(m-1\right)+3}{m^2+2}=\frac{2m+1}{m^2+2}\)

mik chịu

Mình vẽ tạm trên Paint vì không biết vẽ nửa đường tròn trên đây nha '-'

Bài làm

a) Vì M là giao điểm của hai tiếp tuyến MN và Ax

=> OM là phân giác 

=> \(\widehat{O_2}=\widehat{O_3}\Rightarrow2\widehat{O_2}=\widehat{HOA}\)   

Vì N là giao điểm của hai tiếp tuyến MN và By

=> ON là phân giác

=> \(\widehat{O_1}=\widehat{O_4}\Rightarrow2\widehat{O_1}=\widehat{HOB}\)

Ta có: \(\widehat{HOA}+\widehat{HOB}=180^0\)(hai góc kề bù)

hay \(2\widehat{O_1}+2\widehat{O_2}=180^0\)

=> \(2\left(\widehat{O_1}+\widehat{O_2}\right)=180^0\)

=> \(\widehat{MON}=\frac{180^0}{2}=90^0\)

Vậy \(\widehat{MON}=90^0\)

b)  Vì M là giao điểm của hai tiếp tuyến MN và Ax

=> AM = MH ( tính chất hai tiếp tuyến cắt nhau)

Vì N là giao điểm của hai tiếp tuyến MN và By

=> NB = NH (tính chất hai tiếp tuyến cắt nhau)

Ta có: MN = MH + NH

hay MN = AM + BN (đpcm)

c) Xét tam giác MON vuông tại O có:

OH là đường cao

Theo quan hệ giữa cạnh và đường cao

=> OH² = MH . NH

hay R² = MA . BN

Vậy AM . BN = R²

Đề bạn rối sao ý, mình chỉnh như này không biết có đúng không nhưng mình sẽ làm theo đề mình đưa ra:

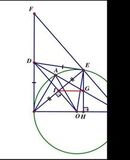
Cho (O) và điểm A ∉ (O) sao cho OA = 2R. Vẽ tiếp tuyến AB với (O), BH là đường cao của △ABO, BH cắt (O) tại C.

*Hình:

O A B H C d K E G I

Bài làm

a) Xét đường tròn tâm O có:

CB là dây cung

OA vuông góc với CB tại H

=> H là trung điểm CB (Tính chất đường cao với dây cung)

Xét tam giác ABC có:

AH là đường cao

AH là trung tuyến (Do H là trung điểm CB)

=> Tam giác ABC cân tại A

=> AB  = AC

Xét tam giác OCA và tam giác OBA có:

AC = AB (Chứng minh trên)

OA chung

OC = OB (bằng R)

=> Tam giác OCA = tam giác OBA (c.c.c)

=> \(\widehat{ABO}=\widehat{ACO}\)

Mà \(\widehat{ABO}=90^0\)

=> \(\widehat{ACO}=90^0\)

Và C thuộc (O)

=> AC là tiếp tuyến của (O)

b) Kẻ KE vuông góc với OA cắt (O) tại E.

Vì A là giao điểm của hai đường tiếp tuyến AB và AC

=> AO là phân giác của góc AOB

Xét tam giác KAE có:

AO là phân giác của góc AOB

AO vuông góc với KE

=> Tam giác KAE cân tại A

=> AK = AE (1)

=> AO là trung tuyến

Gọi giao điểm của AO và KE là G

=> KG = GE

Xét tam giác KGO và tam giác EGA có:

\(\widehat{OKG}=\widehat{GEA}\)(Là hai góc so le trong do OK // AB vì cùng vuông góc với OB.)

KG = GE (Chứng minh trên)

\(\widehat{KGO}=\widehat{EGA}\)(đối)

=> Tam giác KGO = tam giác EGA (g.c.g)

=> OK = AE (2)

Từ (1) và (2) => KA = KO

Từ từ để mình nghĩ nốt c với d