x=y=z=2

b) Xét phương trình 2 có 
(1-x² )/(1+xy)² - (x+y)²    - y² =1
=>(1-x²)/1+2xy+x²y²-x²-2xy-y²   -y²=1
=>(1-x²) /(1-x² )-y²(1-x²)       -y² =1
=>(1-x²)/(1-x²)(1-y²)       -y²=1
=>1/(1-y²)    -y²=1
=>1=(1-y²)²
=>1=1-2y²+y4
=>y⁴-2y²=0
=>y²(y²-2)=0
=>y=0
y²-2=0
=> y=+√2
=> y=-√2
 Thay y vào phương trình 1 là ra x 

à nhầm ... sửa lại dòng 6 
=> 1/(1-y²) - y²=1
=> 1/(1-y²)=1+y²
=> 1=1-y⁴
=> y=0
=>x=3
=> x=-3
 

\(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+3y^3=2023\)

\(\Leftrightarrow\left[\left(x+1\right)\left(x+7\right)\right]\left[\left(x+3\right)\left(x+5\right)\right]+3y^3=2023\)

\(\Leftrightarrow\left(x^2+8x+7\right)\left(x^2+8x+15\right)+3y^3=2023\)  (*)

Đặt \(x^2+8x+11=t\left(t\inℤ;t\ge-5\right)\), pt (*) trở thành \(\left(t-4\right)\left(t+4\right)+3y^3=2023\) 

\(\Leftrightarrow t^2-16+3y^3=2023\)

\(\Leftrightarrow t^2+3y^3=2039\)        (1)

Xét pt (1), dễ thấy \(t^2\equiv0\left(mod3\right)\) hoặc \(t^2\equiv1\left(mod3\right)\), lại có \(3y^3\equiv0\left(mod3\right)\) nên \(VT\equiv0\left(mod3\right)\) hoặc \(VT\equiv1\left(mod3\right)\). Nhưng \(VP=2039\equiv2\left(mod3\right)\), điều này có nghĩa là (1) vô nghiệm.

Vậy phương trình đã cho không thể có nghiệm nguyên.

(x+1)(x+3)(x+5)(x+7)+3y3=2023

⇔[(�+1)(�+7)][(�+3)(�+5)]+3�3=2023⇔[(x+1)(x+7)][(x+3)(x+5)]+3y3=2023

⇔(�2+8�+7)(�2+8�+15)+3�3=2023⇔(x2+8x+7)(x2+8x+15)+3y3=2023  (*)

Đặt �2+8�+11=�(�∈Z;�≥−5)x2+8x+11=t(t∈Z;t≥−5), pt (*) trở thành (�−4)(�+4)+3�3=2023(t−4)(t+4)+3y3=2023 

⇔�2−16+3�3=2023⇔t2−16+3y3=2023

⇔�2+3�3=2039⇔t2+3y3=2039        (1)

Xét pt (1), dễ thấy �2≡0(���3)t2≡0(mod3) hoặc �2≡1(���3)t2≡1(mod3), lại có 3�3≡0(���3)3y3≡0(mod3) nên $VT\equiv 0\left(mod3\right)$ hoặc $VT\equiv 1\left(mod3\right)$. Nhưng $VP=2039\equiv 2\left(mod3\right)$, điều này có nghĩa là (1) vô nghiệm.

Vậy phương trình đã cho không thể có nghiệm nguyên

em khong biet

a. Khoảng cách từ vật đến thấu kính lớn hơn tiêu cự của thấu kính (d > f)

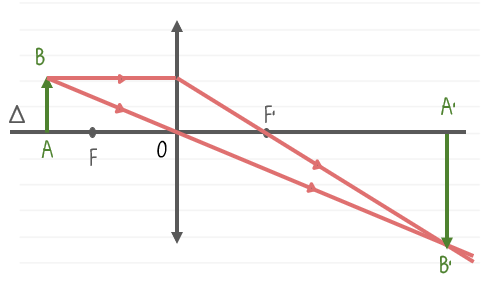
Khi vật đặt ngoài khoảng tiêu cự, ảnh thật ngược chiều với vật. 

b.. Khoảng cách từ vật đến thấu kính nhỏ hơn tiêu cự của thấu kính (d < f).

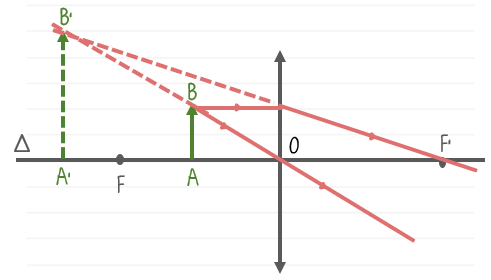
Khi vật đặt trong khoảng tiêu cự, ảnh ảo cùng chiều với vật và lớn hơn vật.

00000000

Hello 

Hello xin chào 

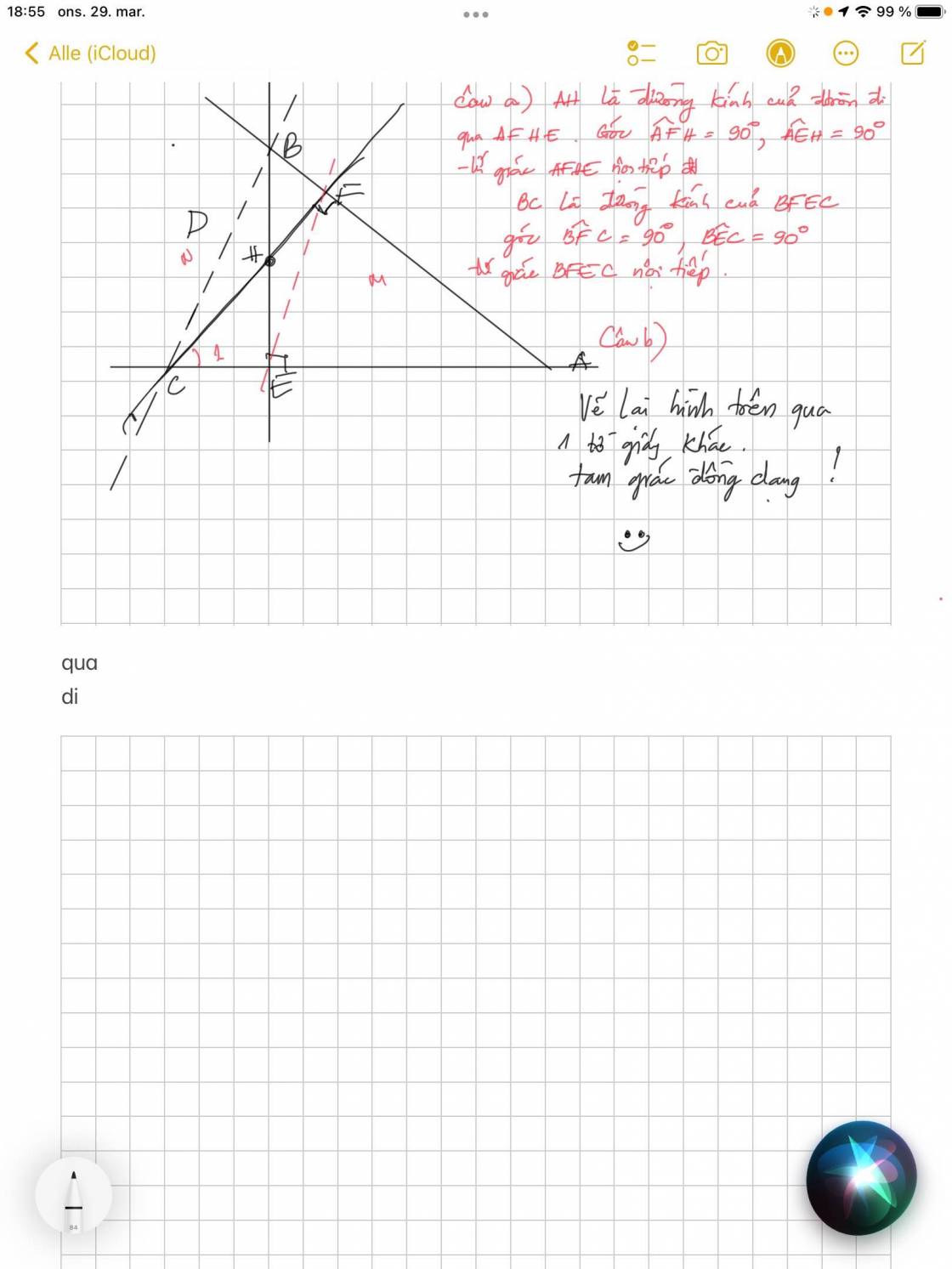
a. Muốn dựng ảnh A'B' của AB qua thấu kính (AB vuông góc với trục chính của thấu kính, A nằm trên trục chính), chỉ cần dựng ảnh B' của B bằng cách vẽ đường truyền của hai trong ba tia sáng đặc biệt, sau đó từ B' hạ vuông góc xuống trục chính ta có ảnh A' của A.

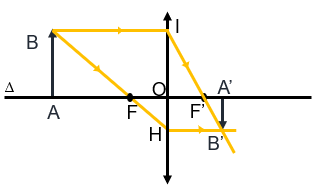
 Ảnh thu được là ảnh thật, ngược chiều vật.

b. $h=2cm;d=36cm;f=12cm$

Xét $\Delta ABF$ đồng dạng với $\Delta OHF$, ta có: \dfrac{AB}{OH}=\dfrac{AF}{OF}OHAB​=OFAF​

Vì OH=A'B'OH=A′B′ \Rightarrow\dfrac{AB}{A'B'}=\dfrac{AF}{OF}\Rightarrow\dfrac{h}{h'}=\dfrac{d-f}{f}⇒A′B′AB​=OFAF​⇒h′h​=fd−f​

\Rightarrow h'=\dfrac{hf}{d-f}=\dfrac{2.12}{36-12}=1cm⇒h′=d−fhf​=36−122.12​=1cm

Xét \Delta OIF'ΔOIF′ đồng dạng với \Delta A'B'F'ΔA′B′F′, ta có: \dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}A′B′OI​=A′F′OF′​

Vì OI=AB\Rightarrow\dfrac{AB}{A'B'}=\dfrac{OF'}{A'F'}\Rightarrow\dfrac{h}{h'}=\dfrac{f}{A'F'}OI=AB⇒A′B′AB​=A′F′OF′​⇒h′h​=A′F′f​

\Rightarrow A'F'=\dfrac{h'f}{h}=\dfrac{1.12}{2}=6cm⇒A′F′=hh′f​=21.12​=6cm

d'=OF'+A'F'=12+6=18cmd′=OF′+A′F′=12+6=18cm

Vậy ảnh A'B' cách thấu kính 18 cm và cao 1 cm.

a. ARN được tổng hợp theo 2 nguyên tắc là nguyên tắc bổ sung và nguyên tắc khuôn mẫu, ARN là bản sao của một đoạn ADN (tương ứng với một gen), ngoài ra ở một số virut ARN là vật chất di truyền.

Nôi dung nguyên tắc bổ sung: Trong di truyền học, sinh học phân tử, nguyên tắc bổ sung là nguyên tắc liên kết giữa một nucleotide và một nucleotide khác đối diện, trong các đại phân tử DNA hay RNA.

Nội dung nguyên tắc khuôn mẫu: các mạch ADN của mẹ làm mạch khuôn để tổng hợp mạch ADN mới (có ở nhân đôi ADN)

a) Điện trở tương đương của mạch là:

R_tđ=R₁+R₂=25+15=40 (Ω)

Cường độ dòng điện đi qua mỗi điện trở là:

I₁=I₂=I=U/R_tđ=12/40=0,3 (A)

b) Điện trở của R₂ là:

R₂=\(\dfrac{\rho\times l}{S}\)=15 (Ω)

<=> \(\dfrac{0,5\times10^{-6}\times l}{0,06\times10^{-6}}\)=15

<=>0,5.l=0,9

<=>l=1,8 (m)

c) Hiệu điện thế hai đầu R₂ là :

U₂=U-Uđ=12-6=6 (V)

Cường độ dòng điện đi qua R₁ là:

I₁=\(\dfrac{U_đ}{R_1}=\dfrac{6}{25}=0,24\) (A)

Cường độ dòng điện đi qua đèn là:

Iđ=\(\dfrac{P_đ}{U_đ}=\dfrac{3}{6}=0,5\)  (A)

Cường độ dòng điện đi qua R₂ là:

I₂=I=Iđ+I₁=0,5+0,24=0,74 (A)

Điện trở của R₂ lúc đó là:

R₂=U₂/I₂=6/0,74≈8,11 (Ω)

a)\(R_1ntR_2\Rightarrow\)\(R_tđ=R_1+R_2=25+15=40\)\(\Omega\)

\(I_1=I_2=I=\dfrac{U}{R_{tđ}}=\dfrac{12}{40}=0,3A\)

b)Điện trở dây: \(R=\rho\cdot\dfrac{l}{S}\)

\(\Rightarrow\)Chiều dài dây: \(l=\dfrac{R\cdot S}{\rho}=\dfrac{15\cdot0,06\cdot10^{-6}}{0,5\cdot10^{-6}}=1,8m\)

c)\(R_Đ=\dfrac{U^2_Đ}{P_Đ}=\dfrac{6^2}{3}=12\Omega;I_{Đđm}=\dfrac{P_Đ}{U_Đ}=\dfrac{3}{6}=0,5A\)

CTM: \(\left(R_1//Đ\right)ntR_2\)

Để đèn sáng bình thường\(\Rightarrow I_Đ=I_{Đđm}=0,5A\Rightarrow U_Đ=0,5\cdot12=6V\Rightarrow U_{1Đ}=6V\)

\(U_1=6V\Rightarrow I_1=\dfrac{6}{25}=0,24A\)

\(I_2=I_1+I_Đ=0,24+0,5=0,74A\)

\(U_2=U-U_{1Đ}=12-6=6V\)

\(R_2=\dfrac{U_2}{I_2}=\dfrac{6}{0,74}=\dfrac{300}{37}\approx8,108\Omega\)

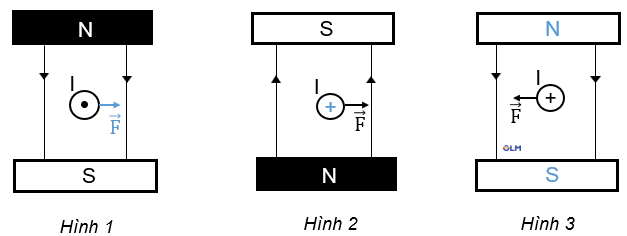
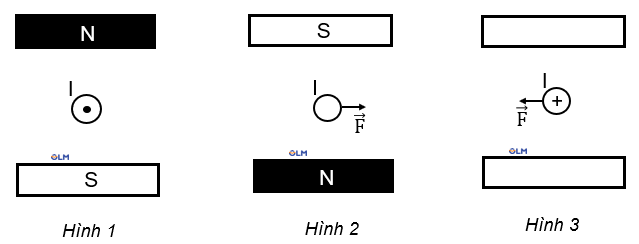
a. Quy tắc bàn tay trái: Đặt bàn tay trái sao cho các đường sức từ hướng vào lòng bàn tay, chiều từ cổ tay đến ngón tay giữa hướng theo chiều dòng điện thì ngón tay cái choãi ra 90° chỉ chiều của lực điện từ.

a. Quy tắc xác định chiều của lực điện từ (Quy tắc bàn tay trái): Đặt bàn tay trái sao cho các đường sức từ hướng vào lòng bàn tay, chiều từ cổ tay đến ngón tay giữa hướng theo chiều dòng điện thì ngón tay cái choãi ra 90o chỉ chiều của lực điện từ.

b. Hình 1 cần xác định chiều lực từ tác dụng lên dây dẫn.