cho hình thang abcd có ab//cd, đường cao bằng 4cm,đường chéo bd=5cm,hai đường chéo ac và bd vuông góc với nhau, tính diện tính hình thang abcd
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng quát:
\(\frac{1}{\sqrt{n}}=\frac{2}{\sqrt{n}+\sqrt{n}}>\frac{2}{\sqrt{n}+\sqrt{n+1}}=\frac{2\left(\sqrt{n+1}-\sqrt{n}\right)}{n+1-n}=2\left(\sqrt{n+1}-\sqrt{n}\right)\)
\(\frac{1}{\sqrt{n}}=\frac{2}{\sqrt{n}+\sqrt{n}}< \frac{2}{\sqrt{n}+\sqrt{n-1}}=\frac{2\left(\sqrt{n}-\sqrt{n-1}\right)}{n-\left(n-1\right)}=2\left(\sqrt{n}-\sqrt{n-1}\right)\)
Suy ra: \(2\left(\sqrt{n+1}-\sqrt{n}\right)< \frac{1}{\sqrt{n}}< 2\left(\sqrt{n}-\sqrt{n-1}\right)\)
\(A=1+\frac{1}{\sqrt{2}}+...+\frac{1}{\sqrt{100}}< 1+2\left(\sqrt{2}-\sqrt{1}+...+\sqrt{100}-\sqrt{99}\right)\)
\(=1+2\left(\sqrt{100}-\sqrt{1}\right)=19\)
\(A=1+\frac{1}{\sqrt{2}}+...+\frac{1}{\sqrt{100}}>2\left(\sqrt{2}-\sqrt{1}+\sqrt{3}-\sqrt{2}+...+\sqrt{100}-\sqrt{99}\right)\)
\(=2\left(\sqrt{100}-\sqrt{1}\right)=18\)
Do đó ta có đpcm.

Xét tam giác \(BGA\)vuông tại \(G\):
\(BA^2=BG^2+GA^2=\frac{4}{9}\left(BE^2+AM^2\right)\Leftrightarrow BE^2+\frac{BC^2}{4}=\frac{27}{2}\)(1)
Xét tam giác \(ABE\)vuông tại \(A\):
\(BE^2=AB^2+AE^2=6+\frac{1}{4}AC^2\)(2)
Từ (1) và (2) suy ra \(BC^2+AC^2=30\)
mà \(BC^2=AC^2+6\)
suy ra \(BC^2=18\Rightarrow BC=3\sqrt{2}\left(cm\right)\).

ĐK: \(y\ne0,xy\ge0\).
\(4x^2+9y^2=16xy\)
Chia cả hai vế cho \(y^2\)ta được:
\(4\left(\frac{x}{y}\right)^2+9=\frac{16x}{y}\)
\(\Leftrightarrow\frac{x}{y}=\frac{4\pm\sqrt{7}}{2}\)
Với \(y>0\)thì \(x\ge0\)
\(P=\frac{\sqrt{xy}+\sqrt{y^2}}{y}-\sqrt{\frac{x}{y}}=\frac{\sqrt{x}\sqrt{y}+y}{y}-\sqrt{\frac{x}{y}}=\sqrt{\frac{x}{y}}+1-\sqrt{\frac{x}{y}}=1\)
Với \(y< 0\)thì \(x\le0\):
\(P=\frac{\sqrt{xy}+\sqrt{y^2}}{y}-\sqrt{\frac{x}{y}}=\frac{\sqrt{-x}\sqrt{-y}-y}{y}-\sqrt{\frac{x}{y}}=-\sqrt{\frac{x}{y}}-1-\sqrt{\frac{x}{y}}=-2\sqrt{\frac{x}{y}}-1\)
\(=-2\sqrt{\frac{4\pm\sqrt{7}}{2}}-1=-\left(1\pm\sqrt{7}\right)-1=-2\pm\sqrt{7}\)

+) Xét n≥27n≥27
Ta có : A=427+42016+4n=427⋅(1+41989+4n−27)A=427+42016+4n=427⋅(1+41989+4n−27)
Dễ thấy 427=22⋅27=(227)2427=22⋅27=(227)2 là số chính phương
Do đó để A là số chính phương thì 1+41989+4n−271+41989+4n−27 là số chính phương
Đặt B2=1+41989+4n−27B2=1+41989+4n−27 và n−27=kn−27=k
Khi đó : B2=1+41989+4kB2=1+41989+4k
⇔B2−(2k)2=1+41989⇔B2−(2k)2=1+41989
⇔(B−2k)(B+2k)=1+41989⇔(B−2k)(B+2k)=1+41989
Ta có : B+2k≤1+41989B+2k≤1+41989 và B−2k≥1B−2k≥1
⇒B−2k+41989≥1+41989≥B+2k⇒B−2k+41989≥1+41989≥B+2k
Hay B−2k+41989≥B+2kB−2k+41989≥B+2k
⇔2⋅2k≤41989⇔2⋅2k≤41989
⇔2k+1≤23978⇔2k+1≤23978
⇔k+1≤3978⇔k+1≤3978
⇔k≤3977⇔k≤3977
Để n lớn nhất thì k lớn nhất,nên:
Nếu k=3977k=3977 ta có B2=1+41989+43977B2=1+41989+43977
⇔B2=(23977)2+2⋅23977+1⇔B2=(23977)2+2⋅23977+1
⇔B2=(23977+1)2⇔B2=(23977+1)2( đúng )
Vậy k=3977⇒n=3977+27=4004k=3977⇒n=3977+27=4004( thỏa )
+) Xét n≤27n≤27 nên hiển nhiên n≤4004n≤4004
Suy ra n lớn nhất để A là số chính phương thì n=4004
Nếu thấy đúng thì k cho mình nha
\(A=4^{27}+4^{2016}+4^n\)
Với \(n\ge27\):
\(A=4^{27}\left(1+4^{1989}+4^{n-27}\right)\)
\(A\)là số chính phương suy ra \(B=4^{n-27}+4^{1989}+1\)là số chính phương.
\(B=\left(2^{n-27}\right)^2+2^{3978}+1\)
\(=\left(2^{3977+n-4004}\right)^2+2.2^{3977}+1\)
Với \(n=4004\)thì:
\(B=\left(2^{3977}\right)^2+2.2^{3977}+1=\left(2^{3977}+1\right)^2\)là số chính phương.
Với \(n>4004\)thì:
\(B>\left(2^{3977+n-4004}\right)^2\)
\(B< \left(2^{3977+n-4004}\right)^2+2.2^{3977+n-4004}+1\)
\(=\left(2^{3977+n-4004}+1\right)^2\)
Suy ra \(\left(2^{3977+n-4004}\right)^2< B< \left(2^{3977+n-4004}+1\right)^2\)do đó \(B\)không là số chính phương.
Vậy giá trị lớn nhất của \(n\)là \(4004\).

\(n^2+2n+\sqrt{n^2+2n+18}+9\)là số chính phương thì \(\sqrt{n^2+2n+18}\)là số tự nhiên.
Khi đó \(n^2+2n+18=m^2\)
\(\Leftrightarrow\left(m-n-1\right)\left(m+n+1\right)=1.17\)
Do \(m,n\)là số tự nhiên nên
\(\hept{\begin{cases}m-n-1=1\\m+n+1=17\end{cases}}\Leftrightarrow\hept{\begin{cases}m=9\\n=7\end{cases}}\)
Với \(n=7\)thì \(n^2+2n+\sqrt{n^2+2n+18}+9=7^2+2.7+\sqrt{7^2+2.7+18}+9\)
\(=81=9^2\)là số chính phương (thỏa mãn).
Vậy \(n=7\).

\(2\ge2x+3y\ge2\sqrt{2x.3y}\Rightarrow xy\le\frac{1}{6}.\)
\(A=\frac{4}{4x^2+9y^2}+\frac{9}{xy}=\frac{4}{4x^2+9y^2}+\frac{4}{12xy}+\frac{26}{3xy}\ge\frac{\left(2+2\right)^2}{4x^2+9y^2+12xy}+\frac{26}{3xy}\)
\(\ge\frac{4^2}{2^2}+\frac{26}{3.\frac{1}{6}}=56\)
Dấu \(=\)khi \(\hept{\begin{cases}\frac{2}{4x^2+9y^2}=\frac{2}{12xy}\\2x=3y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{1}{3}\end{cases}}\)
Áp dụng bất đẳng thức Cô – si cho hai số dương, ta có: 2x + 3y ≥ 2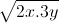
⇔ 2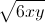 ≤ 2x + 3y
≤ 2x + 3y
Mà 2x + 3y ≤ 2
Do đó 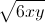 ≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
A = 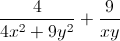 = 4(
= 4(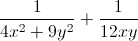 ) +
) + 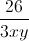 ≥ 4
≥ 4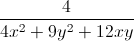 +
+ 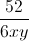 = 16
= 16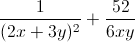 ≥ 16.
≥ 16.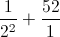 = 56
= 56
Dấu “ = “ xảy ra ⇔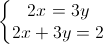 ⇔
⇔ 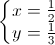
Vậy giá trị nhỏ nhất của biểu thức A là 56.

sửa đề : \(\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)
\(=\sqrt{5^2+2.5\sqrt{2}+2}-\sqrt{4^2+2.4\sqrt{2}+2}\)
\(=\sqrt{\left(5+\sqrt{2}\right)^2}-\sqrt{\left(4+\sqrt{2}\right)^2}=\left|5+\sqrt{2}\right|-\left|4+\sqrt{2}\right|\)
\(=5+\sqrt{2}-4-\sqrt{2}=1\)
=1 nha
t.i.c.k mình nha
bạn nào 10sp gúp mình đi

\(\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\frac{\sqrt{2}+\sqrt{3}+2+2+\sqrt{2}\sqrt{3}+\sqrt{2}\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\left(1+\sqrt{2}\right)\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=1+\sqrt{2}\)

\(x=\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4+\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8+2\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)\)
\(=2\)
Với \(x=2\):
\(\frac{\sqrt{\frac{1}{x}+4+4x}}{\sqrt{x}\left(2x^2-x-1\right)}=\frac{\sqrt{\frac{1}{2}+4+8}}{\sqrt{2}\left(8-2-1\right)}=\frac{1}{2}\)
Dựng hình bình hành \(ABEC\).
Khi đó \(E\in DC\).
Vì \(BD\perp AC\)mà \(AC//BE\)nên \(BE\perp BD\).
Kẻ \(BH\perp DE\).
Xét tam giác \(BED\)vuông tại \(B\)đường cao \(BH\):
\(\frac{1}{BH^2}=\frac{1}{BD^2}+\frac{1}{BE^2}\Leftrightarrow\frac{1}{4^2}=\frac{1}{5^2}+\frac{1}{BE^2}\Leftrightarrow BE=\frac{20}{3}\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.BD.BE=\frac{1}{2}.5.\frac{20}{3}=\frac{50}{3}\left(cm^2\right)\)
Có ai biết đổi tên cho mình hông?