Xin lỗi bạn , mình mới học lớp 5 thôi nên cũng không biết gì ...

~~~ Chúc bạn học giỏi ~~~

Mình cũng mới lớp 5 thôi.

  Mong bạn làm được !

A B C H K D 1 1 2 2

a) Xét \(\Delta KAC\)và \(\Delta HAB\)có:

\(\widehat{A}\)chung

\(AC=AB\)(vì \(\Delta ABC\)cân tại A)

\(\widehat{AKC}=\widehat{AHB}\left(=90^0\right)\)

\(\Rightarrow\Delta KAC=\Delta HAB\left(g.c.g\right)\)

\(\Rightarrow CK=BH\)(2 cạnh tương ứng) (điều phải chứng minh)

b) \(\Delta KAC=\Delta HAB\)(theo câu a))

\(\Rightarrow KA=HA\)(2 cạnh tương ứng)

\(\Rightarrow\Delta AHK\)cân tại A (điều phải chứng minh)

Lại \(\Delta KAC=\Delta HAB\)(theo câu a))

\(\Rightarrow\widehat{C_1}=\widehat{B_1}\)(2 góc tương ứng)

Ta có: \(\widehat{ABC}=\widehat{ACB}\)(vì \(\Delta ABC\)cân tại A)

Mà \(\widehat{B_1}+\widehat{B_2}=\widehat{ABC};\widehat{C_1}+\widehat{C_2}=\widehat{ACB}\)

\(\Rightarrow\widehat{B_1}+\widehat{B_2}=\widehat{C_1}+\widehat{C_2}\)

Mà \(\widehat{B_1}=\widehat{C_1}\)(chứng minh trên)

\(\Rightarrow\widehat{B_2}=\widehat{C_2}\)\(\Rightarrow\Delta DBC\)cân tại D (điều phải chứng minh)

-Dạng 1: Phương trình tích.

a) \(2x\left(x+1\right)=x^2-1\)\(\Leftrightarrow2x\left(x+1\right)=\left(x-1\right)\left(x+1\right)\)

\(\Leftrightarrow2x\left(x+1\right)-\left(x-1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(2x-x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)^2=0\)

\(\Leftrightarrow x+1=0\Leftrightarrow x=-1\)

Vậy phương trình có nghiệm duy nhất : x = -1

b) \(x^3+3x^2-2x-2=0\)\(\Leftrightarrow\left(x^3-x^2\right)+\left(4x^2-4x\right)+\left(2x-2\right)=0\)

\(\Leftrightarrow x^2\left(x-1\right)+4x\left(x-1\right)+2\left(x-1\right)=0\)

\(\Leftrightarrow\left(x^2+4x+2\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[\left(x+2\right)^2-2\right]\left(x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}\left(x+2\right)^2-2=0\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}\left(x+2\right)^2=2\\x=1\end{cases}}}\)

Xét phương trình \(\left(x+2\right)^2=2\)

\(\Leftrightarrow\orbr{\begin{cases}x+2=\sqrt{2}\\x+2=-\sqrt{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\sqrt{2}-2\\x=-\sqrt{2}-2\end{cases}}}\)

Vậy phương trình có tập nghiệm : \(S=\left\{1;\pm\sqrt{2}-2\right\}\)

Dạng 2  ; Phương trình chứa ẩn ở mẫu.

\(\frac{3}{1-5x}+\frac{5}{3-5x}=\frac{x-27}{\left(5x-1\right)\left(5x-3\right)}\left(ĐKXĐ:x\ne\frac{1}{5};x\ne\frac{3}{5}\right)\)

\(\Leftrightarrow\frac{3}{1-5x}+\frac{5}{3-5x}=\frac{x-27}{\left(1-5x\right)\left(3-5x\right)}\)(phần này bạn nhớ đọc kĩ bên vế phải)

\(\Leftrightarrow\frac{3\left(3-5x\right)}{\left(1-5x\right)\left(3-5x\right)}+\frac{5\left(1-5x\right)}{\left(3-5x\right)\left(1-5x\right)}=\frac{x-27}{\left(1-5x\right)\left(3-5x\right)}\)

\(\Rightarrow3\left(3-5x\right)+5\left(1-5x\right)=x-27\)

\(\Leftrightarrow9-15x+5-25x=x-27\)

\(\Leftrightarrow14-40x=x-27\)

\(\Leftrightarrow-40x-x=-27-14\)

\(\Leftrightarrow-41x=-41\)

\(\Leftrightarrow x=1\)(thỏa mãn ĐKXĐ)

Vậy phương trình có nghiệm duy nhất : x = 1.

\(M=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...-\frac{1}{2018}+\frac{1}{2019}\)

\(M=\left(1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{2019}\right)-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...+\frac{1}{2018}\right)\)

\(M=\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2018}+\frac{1}{2019}\right)-2\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...+\frac{1}{2018}\right)\)

\(M=\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2019}\right)-\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{1009}\right)\)

\(M=\frac{1}{1010}+\frac{1}{1011}+...+\frac{1}{2019}=N\)

Suy ra \(\left(M-N\right)^2=0\).

\(\left(\frac{1}{a};\frac{1}{b};c\right)=\left(x;y;z\right)\)\(\Rightarrow\)\(x+y+z\le2\)

\(P=\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}+x+y+z=\Sigma\left(\frac{1}{x^2}+\frac{27}{8}x+\frac{27}{8}x\right)-\frac{23}{4}\left(x+y+z\right)\ge\frac{35}{4}\)

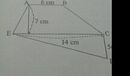
Diện tích hình thang \(ABCE\)là: 

\(\left(14+6\right)\div2\times7=70\left(cm^2\right)\)

Diện tích tam giác \(DCE\)là: 

\(5\times14\div2=35\left(cm^2\right)\)

Diện tích \(ABCDE\)là: 

\(70+35=105\left(cm^2\right)\)

Dịch dấu phẩy sang phải một hàng thì số mới hơn 10 lần số cũ.

   Ta có sơ đồ:

    Số cũ: -----

                                                 Hiệu: 47,34

    Số mới: ----- ----- ----- ----- ----- ----- ----- ----- ----- -----

    Số phải tìm là: 47,34:[10-1]=5,26

                                Đ/S:5,26

Dạng bài tổng tỉ nha

a/ Ta có

\(AB\perp AC;CE\perp AC\) => AB//CE \(\Rightarrow\widehat{ABD}=\widehat{BEC}\) (Góc so le trong) (1)

\(\widehat{ABD}=\widehat{EBC}\) (Đề bài) (2)

Từ (1) và (2) \(\Rightarrow\widehat{BEC}=\widehat{EBC}\) => tam giác BCE cân tại C

b/ Do tam giác BCE cân tại C => CE=BC

Mà trong tam giác vuông ABC có BC>AB (trong tg vuông cạnh huyền là cạnh lớn nhất) => CE>AB

mình k có bạn

Ta có: dài hcn 100% ; rộng hcn 100%

CD sau khi tăng: 100%+10%=110% 

CR sau khi giảm: 100%-10%=90%

S hcn ban đầu: 100% x 99%=99%

Vì 99%<100% nên S hcn giảm đi 1%

     ĐS: 1%

Cái kia sai nhá bạn

Gọi số đo chiều dài là 100 x a

                 Số đo chiều rộng là 100 x b

          Số đo diện tích là : 10 000 x a x b

          Số đo chiều dài mới là : 110 x a

         số đo chiều rộng mới là :  90 x b

          Số đo diện tích  mới là : 9900 x a x b

          Số đo diện tích mới kém số đo diện tích cũ là :

                   10 000 x a x b – 9 900 x a x b = 100 x a x b

            Tức là kém diện tích cũ là :   100 × a × b 1000 × a × b =10%