Trên các cạnh BC và CD của hình vuông ABCD lấy các điểm E và F sao cho góc EAF 45 độ. Các đoạn thẳng AE,AF cắt BD theo thứ tự tại H và K. Chứng minh tứ giác EHKF nội tiếp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

LB
Lê Bích Ngọc
5 tháng 3 2021
Đây nha bạn.học tốt😊

Đúng(0)
PD
Phạm Đình Khoẻ
5 tháng 3 2021
Hình như Lê Bích Ngọc tra mạng hay sao đó
Đúng(0)

5 tháng 3 2021
a.Xét hai tam giác vuông ABE và tam giác vuông KBE có
góc ABE = góc KBE = 90độ
cạnh BE chung
góc ABE = góc KBE [ gt ]
Do đó ; tam giác ABE = tam giác KBE [ g.c.g ]
⇒
AB = KB [ cạnh tương ứng ]
Vậy tam giác ABK cân tại B
b.Xét tam giác ABD và tam giác KBD có
AB = KB [ vì tam giác ABE = tam giác KBE theo câu a ]
góc ABD = góc KBD [ vì BD là tia phân giác góc B ]
cạnh BD chung
Do đó ; tam giác ABD = tam giác KBD [ c.g.c ]
⇒
góc BAD = góc BKD [ góc tương ứng ]
mà bài cho góc BAD = 90độ nên góc KBD = 90độ
Vậy DK vuông góc với BC
c.Vì DK vuông góc với BC và AH vuông góc với BC nên
DK // AH
Suy ra ; góc HAK = góc DKA [ ở vị trí so le trong ] [ 1 ]
Mặt khác ; AD = DK [ vì tam giác ABD = tam giác KBD ]
⇒
tam giác ADK là tam giác cân tại D nên
góc DKA = góc DAK [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra
góc HAK = góc DAK

5 tháng 3 2021
bài 1
vì M thuộc đường tròn tâm C đường kính AB nen ta có CA=CM=CB=R
vậy tam giác CAM cân tại C và tam giác CBM cân tại C
vì tam giác CAM cân tại C nên ta có góc CMA = góc CAM = (180-góc ACM):2
vì tam giác CBM cân tại C nên ta có góc CBM= góc CMB= (180-góc BCM):2
ta lại có góc AMB= góc AMC + góc BMC=
180
−
g
ó
c
A
C
M
2
+
180
−
g
ó
c
B
C
M
2
=
180
+
180
−
g
ó
c
A
C
M
−
g
ó
c
B
C
M
2
=
360
−
g
ó
c
A
C
B
2
=
360
−
180
2
=90 độ

5 tháng 3 2021
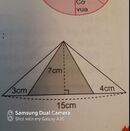
Diện tích 1 mặt là :
1,5.2=3 (m2)
Diện tích xung quanh là :
4.3=12(m2)
Diện tích bể là :
12+3=15(m2)
Dổi 15m2= 1500 cm2
Số gạch cần dùng là:
1500:20=75 (viên)
Đáp số 75 viên
L
108


4 tháng 3 2021
ta có
((x-a)(x-b))/((c-a)(c-b))+((x-b)(x-c))/((a-b)(a-c))+((x-c)(x-a))/((b-c)(b-a))=(( x-a)(x-b)(b-a)+(x-b)(x-c)(c-b)-(x-c)(x-a)(c-a))/((c-a)(c-b)(b-a))
=> mẫu là (c-a)(c-b)(b-a) (1)
ta có (x-a)(x-b)(b-a)
= (x-a)(x-b)( b-c+c-a)
=(x-a)(x-b)(b-c) + (x-a)(x-b)(c-a)
=> phần tử : (x-a)(x-b)(b-c)+ (x-b)(x-c)(c-b) + (x-a)(x-b)(c-a)- (x-c)(x-a)(c-a)
=(b-c)(x-b)(x-a-x+c) + (x-a)(c-a)(x-b-x+c)
=(c-a)(b-c)(x-b) +(x-a)(c-a)(c-b)
=(c-a)(c-b)(-x+b+x-a)=(c-a)(c-b)(b-a) (2)
từ (1);(2)=> tử/mẫu= ((c-a)(c-b)(b-a))/((c-a)(c-b)(b-a))=1 (đpcm)