Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Xét n≥27n≥27
Ta có : A=427+42016+4n=427⋅(1+41989+4n−27)A=427+42016+4n=427⋅(1+41989+4n−27)
Dễ thấy 427=22⋅27=(227)2427=22⋅27=(227)2 là số chính phương
Do đó để A là số chính phương thì 1+41989+4n−271+41989+4n−27 là số chính phương
Đặt B2=1+41989+4n−27B2=1+41989+4n−27 và n−27=kn−27=k
Khi đó : B2=1+41989+4kB2=1+41989+4k
⇔B2−(2k)2=1+41989⇔B2−(2k)2=1+41989
⇔(B−2k)(B+2k)=1+41989⇔(B−2k)(B+2k)=1+41989
Ta có : B+2k≤1+41989B+2k≤1+41989 và B−2k≥1B−2k≥1
⇒B−2k+41989≥1+41989≥B+2k⇒B−2k+41989≥1+41989≥B+2k
Hay B−2k+41989≥B+2kB−2k+41989≥B+2k
⇔2⋅2k≤41989⇔2⋅2k≤41989
⇔2k+1≤23978⇔2k+1≤23978
⇔k+1≤3978⇔k+1≤3978
⇔k≤3977⇔k≤3977
Để n lớn nhất thì k lớn nhất,nên:
Nếu k=3977k=3977 ta có B2=1+41989+43977B2=1+41989+43977
⇔B2=(23977)2+2⋅23977+1⇔B2=(23977)2+2⋅23977+1
⇔B2=(23977+1)2⇔B2=(23977+1)2( đúng )
Vậy k=3977⇒n=3977+27=4004k=3977⇒n=3977+27=4004( thỏa )
+) Xét n≤27n≤27 nên hiển nhiên n≤4004n≤4004
Suy ra n lớn nhất để A là số chính phương thì n=4004
Nếu thấy đúng thì k cho mình nha
\(A=4^{27}+4^{2016}+4^n\)
Với \(n\ge27\):
\(A=4^{27}\left(1+4^{1989}+4^{n-27}\right)\)
\(A\)là số chính phương suy ra \(B=4^{n-27}+4^{1989}+1\)là số chính phương.
\(B=\left(2^{n-27}\right)^2+2^{3978}+1\)
\(=\left(2^{3977+n-4004}\right)^2+2.2^{3977}+1\)
Với \(n=4004\)thì:
\(B=\left(2^{3977}\right)^2+2.2^{3977}+1=\left(2^{3977}+1\right)^2\)là số chính phương.
Với \(n>4004\)thì:
\(B>\left(2^{3977+n-4004}\right)^2\)
\(B< \left(2^{3977+n-4004}\right)^2+2.2^{3977+n-4004}+1\)
\(=\left(2^{3977+n-4004}+1\right)^2\)
Suy ra \(\left(2^{3977+n-4004}\right)^2< B< \left(2^{3977+n-4004}+1\right)^2\)do đó \(B\)không là số chính phương.
Vậy giá trị lớn nhất của \(n\)là \(4004\).

Với \(n\ge3\)thì tích của \(n\)số tự nhiên liên tiếp chia hết cho \(3\)
mà \(4^n\equiv1\left(mod3\right),14\equiv2\left(mod3\right)\Rightarrow4^n-14\equiv2\left(mod3\right)\)do đó không thỏa mãn.
Thử trực tiếp với \(n=1\)và \(n=2\)thu được \(n=2\)thỏa mãn.
\(4^2-14=1.2\).
Vậy \(n=2\).

\(n^2+2n+\sqrt{n^2+2n+18}+9\)là số chính phương thì \(\sqrt{n^2+2n+18}\)là số tự nhiên.
Khi đó \(n^2+2n+18=m^2\)
\(\Leftrightarrow\left(m-n-1\right)\left(m+n+1\right)=1.17\)
Do \(m,n\)là số tự nhiên nên
\(\hept{\begin{cases}m-n-1=1\\m+n+1=17\end{cases}}\Leftrightarrow\hept{\begin{cases}m=9\\n=7\end{cases}}\)
Với \(n=7\)thì \(n^2+2n+\sqrt{n^2+2n+18}+9=7^2+2.7+\sqrt{7^2+2.7+18}+9\)
\(=81=9^2\)là số chính phương (thỏa mãn).
Vậy \(n=7\).

Gọi số dãy ghế ban đầu là a [a>0 ,a thuộc N]
=>Số người trên mỗi dãy ghế là : \(\frac{70}{a}\)
Khi bớt đi 2 dãy ghế => Số dãy ghế còn lại là : a-2
Số người trên mỗi dãy ghế lúc đó là : \(\frac{70}{a-2}\)
Theo bài ra ta có : \(\frac{70}{a}+4=\frac{70}{a-2}\)
=> 70[a-2]+4a[a-2]=70a =>35[a-2]+2a[a-2]=35a
=> 35a-70+2a\(^2\)-4a=35a
=> 2a\(^2\)-4a-70=0
=> \(a^2-2a-35=0=>a^2-2a+1-36=0=>\left[a-1^2\right]=36=6^2\). Có 2 trường hợp
Trường hợp 1 : a-1 = -6 => a = - 5 [loại]
Trường hợp 2 : a - 1 = 6 => a = 7
Còn đây bạn làm nốt tiếp
Vậy phòng họp lúc đầu có 7 dãy ghế và 10 người

Dịch:
FACT FILE - TÀI LIỆU THỰC TẾ
Frédéric François Chopin (1810 - 1849)
Giai đoạn đầu đời: sinh năm 1810 ở Warsaw, nổi tiếng là một thần đồng, trưởng thành, hoàn tất việc học âm nhạc và sáng tác nhiều tác phẩm ở Warwaw trước khi rời khỏi Ba Lan vào năm 1830 ở tuổi 20, cư trú tại Paris sau cuộc nổi dậy vào tháng 11 năm 1830, phải chống chọi với tình trạng sức khỏe kém từ khi còn nhỏ.
Tác phẩm tiêu hiểu: 59 mazukas, 27 khúc luyện, 27 khúc dạo, 21 dạ khúc, 20 bản van-sơ, 18 bản polonaise, 4 bản ballade, 3 xô-nát cho piano.
Thành tựu nổi bật: sáng tác ra bản ballade nhạc cụ và đổi mới các bản xô-nát cho piano, van-sơ và khúc dạo.
Kết luận: một trong nhừng nhà soạn nhạc cho piano vĩ đại nhất thuộc trường phái Lãng mạn, những tác phẩm cho piano của ông thường yêu cầu kỹ thuật cao, ông mất tại Paris vào năm 1849 ở tuổi 39.
FACT FILE - TÀI LIỆU THỰC TẾ
LƯU HỮU PHƯỚC (1921 - 1989)
Giai đoạn đầu đời: sinh ngày 12 tháng 12 năm 1921 ở Hậu Giang (Cần Thơ), một nhân vật tiêu biểu cho nền văn hóa, sáng tác rất nhiều ca khúc yêu nước trong thời kỳ chiến tranh, nhạc thiếu nhi và nhạc opera.
Tác phẩm tiêu biểu: Bạch Đằng Giang, Tiếng Gọi Thanh Niên, Giải Phóng Miền Nam
Thành tựu nổi bật: thành viên của Quốc hội, Chủ tịch úy ban Văn hóa và Giáo dục của nước Cộng hòa Xã hội Chủ nghĩa Việt Nam, nhận giải thưởng Hồ Chí Minh sau khi mất.
Kết luận: một trong những nhà văn hóa lỗi lạc nhất trong suốt những năm diễn ra ohong trào giải phóng đất nước, mất ngày 16 tháng 6 năm 1989 tại Thành phố Hồ Chí Minh.
Giải:
Đoạn 1:
Frédéric François Chopin (1810 - 1849), born in Warsaw, was a poe genius. He grew up and completed his music education and composed his early works in Warsaw before moving to Paris in 1830, at the age of 20, a month before the November 1930 uprising. For most of his life, Chopin was in poor health. His masterpieces included 59 mazurkas, 27 Études, 27Preludes, 21 Nocturnes, 20 Waltzes, 18 Polonaises, 4 ballades, 3 piano sonata. His biggest achievement was the invention of the instrumental ballade. He also made major innovations to the piano sonata, waltz, and Preludes. In conclusion, he is one of the greatest roman piano composers. His piano works are love by many people in the world and often technically demanding. Unfortunately, he died when he was only 39, made lots of people in mourning.
Đoạn 2:
Luu Huu Phuoc (1921-1989) is one of the great composers in Viet Nam. He was born in Hau Giang, can Tho. He was famous for composing many lively patrio wartime songs, children songs and occasional opera, which express the country’s fight against French and America. Some of his famous works are Bach Dang Giang, Tieng Goi Thanh nien, Giai phong mien Nam,… Luu Huu Phuoc was the member of National Assembly, Chairman of the committee of Culture and Education. After his death in 1989, he was awarded Ho Chi Minh prize. To sum up, Luu Huu Phuoc was one of the most prominent cultural figures during national liberations movements. On June 26, 1989, he passed away in Ho Chi Minh city.
Luu Huu Phuoc (1921-1989) is one of the great composers in Viet Nam. He was born in Hau Giang, can Tho. He was famous for composing many lively patrio wartime songs, children songs and occasional opera, which express the country’s fight against French and America. Some of his famous works are Bach Dang Giang, Tieng Goi Thanh nien, Giai phong mien Nam,… Luu Huu Phuoc was the member of National Assembly, Chairman of the committee of Culture and Education. After his death in 1989, he was awarded Ho Chi Minh prize. To sum up, Luu Huu Phuoc was one of the most prominent cultural figures during national liberations movements. On June 26, 1989, he passed away in Ho Chi Minh city.
Frédéric François Chopin (1810 - 1849), born in Warsaw, was a poe genius. He grew up and completed his music education and composed his early works in Warsaw before moving to Paris in 1830, at the age of 20, a month before the November 1930 uprising. For most of his life, Chopin was in poor health. His masterpieces included 59 mazurkas, 27 Études, 27Preludes, 21 Nocturnes, 20 Waltzes, 18 Polonaises, 4 ballades, 3 piano sonata. His biggest achievement was the invention of the instrumental ballade. He also made major innovations to the piano sonata, waltz, and Preludes. In conclusion, he is one of the greatest roman piano composers. His piano works are love by many people in the world and often technically demanding. Unfortunately, he died when he was only 39, made lots of people in mourning.

Năm nay mẹ em đã ngoài ba mươi tuổi. Mẹ có một thân hình cân đối, không mập cũng không gầy. Thân hình của mẹ y như các cô người mẫu trong ti vi. Mẹ em cao trên 1m50. Khuôn mặt trái xoan của mẹ không cò đẹp như lúc ở tuổi 20 nữa vì mẹ phải làm lụng vất vả. Mái tóc của mẹ đen óng, suôn mượt và xõa xuống quá eo. Đôi mắt long lanh, sang như ánh sao làm cho gương mặt mẹ trở nên đẹp hơn. Đôi môi của mẹ đã bị khô vì lâu rồi mẹ chưa chăm sóc môi. Mẹ vui vẻ và hay cười, khi cười mẹ để lộ hàm răng trắng tinh. Nụ cười của mẹ luôn rạng rở và duyên dáng. Các cô bạn thời sinh viên của mẹ nói với em: “ Hồi còn là sinh viên mẹ là một trong những hoa khôi của trường ”. Mẹ sỡ hữu một giọng nói nhẹ nhàng và truyền cảm. Những luc bé Mai làm nũng không chịu ngủ thì bé cứ đòi mẹ hát ru. Nhưng mới hát được một nưa thì bé đã ngủ xay. Mẹ đi đứng nhẹ nhàng và cẩm thận. Mỗi lần em bị ốm, mẹ luôn quan tâm, chăm sóc và ngồi bên giường với em. Mẹ là một người mẹ tuyệt vời nhất thế gian. Các bạn ở lớp ai cũng nói em thật hạnh phúc khi có một người mẹ như vậy. Em rất vui và sẽ cố gắng học tập tốt để mẹ vui lòng.
Trong gia đình, ai cũng thương yêu em hết mực, nhưng mẹ là người gần gũi, chăm sóc em nhiều nhất.
Năm nay, mẹ em bốn mươi tuổi. Với thân hình mảnh mai, thon thả đã tôn thêm vẻ đẹp sang trọng của người mẹ hiền từ. Mái tóc đen óng mượt mà dài ngang lưng được mẹ thắt lên gọn gàng. Đôi mắt mẹ đen láy luôn nhìn em với ánh mắt trìu mến thương yêu. Khuôn mặt mẹ hình trái xoan với làn da trắng. Đôi môi thắm hồng nằm dưới chiếc mũi cao thanh tú càng nhìn càng thấy đẹp. Khi cười, nhìn mẹ tươi như đóa hoa hồng vừa nở ban mai. Đôi bàn tay mẹ rám nắng các ngón tay gầy gầy xương xương vì mẹ phải tảo tần để nuôi nấng, dìu dắt em từ thuở em vừa lọt lòng. Mẹ làm nghề nông nhưng mẹ may và thêu rất đẹp. Đặc biệt mẹ may bộ đồ trông thật duyên dáng, sang trọng. Ở nhà, mẹ là người đảm nhiệm công việc nội trợ. Mẹ dạy cho em các công việc nhẹ nhàng như: quét nhà, gấp quần áo... Còn bố thì giúp mẹ giặt đồ, dọn dẹp nhà cửa sạch sẽ. Thỉnh thoảng, mẹ mua hoa về chưng ở phòng khách cho đẹp nhà. Mỗi khi khách đến, mẹ luôn đón tiếp niềm nở, nồng hậu, mời khách đĩa trái cây và nước mát. Mẹ luôn dậy sớm để chuẩn bị bữa ăn sáng cho cả nhà, để hai anh em cùng cắp sách đến trường kịp giờ học. Khi em ốm đau mẹ phải thức suốt đêm để chăm sóc. Mẹ lo thuốc cho em uống kịp thời. Mẹ nấu cháo và bón cho em từng thìa. Tuy công việc đồng áng bận rộn nhưng buổi tối mẹ thường dành khoảng ba mươi phút để giảng bài cho em. Sau đó mẹ chuẩn bị đồ để sáng mai dậy sớm lo buổi sáng cho gia đình. Mẹ rất nhân hậu, hiền từ. Mẹ chưa bao giờ mắng em một lời. Mỗi khi em mắc lỗi, mẹ dịu dàng nhắc nhở em sửa lỗi. Chính vì mẹ âm thầm lặng lẽ dạy cho em những điều hay lẽ phải mà em rất kính phục mẹ. Mẹ em là vậy. Mẹ ơi, con yêu mẹ lắm! Mỗi khi được mẹ ôm ấp trong vòng tay ấm áp của mẹ, con thấy mình thật hạnh phúc vì có mẹ. Mẹ ơi! Có mẹ, con thấy sướng vui. Có mẹ, con thấy ấm lòng. Trong trái tim con, mẹ là tất cả, mẹ là cô tiên tuyệt vời nhất trong cuộc đời con. Con luôn yêu thương mẹ và tự hào vì được làm con của mẹ.
Tấm lòng của mẹ bao la như biển cả đối với con và con hiểu rằng không ai thương con hơn mẹ. Ôi, mẹ kính yêu của con! Con yêu mẹ hơn tất cả mọi thứ trên cõi đời này vì mẹ chính là mẹ của con. "Đi khắp thế gian không ai tốt bằng mẹ...." Con mong sao cho mình mau lớn để có thể giúp cho mẹ đỡ vất vả hơn. Con hứa sẽ chăm học và cố gắng học thật giỏi để báo đáp công ơn sinh thành nuôi nấng con nên người, mẹ ơi.

\(2\ge2x+3y\ge2\sqrt{2x.3y}\Rightarrow xy\le\frac{1}{6}.\)
\(A=\frac{4}{4x^2+9y^2}+\frac{9}{xy}=\frac{4}{4x^2+9y^2}+\frac{4}{12xy}+\frac{26}{3xy}\ge\frac{\left(2+2\right)^2}{4x^2+9y^2+12xy}+\frac{26}{3xy}\)
\(\ge\frac{4^2}{2^2}+\frac{26}{3.\frac{1}{6}}=56\)
Dấu \(=\)khi \(\hept{\begin{cases}\frac{2}{4x^2+9y^2}=\frac{2}{12xy}\\2x=3y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{1}{3}\end{cases}}\)
Áp dụng bất đẳng thức Cô – si cho hai số dương, ta có: 2x + 3y ≥ 2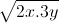
⇔ 2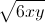 ≤ 2x + 3y
≤ 2x + 3y
Mà 2x + 3y ≤ 2
Do đó 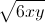 ≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
A = 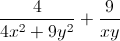 = 4(
= 4(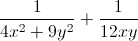 ) +
) + 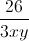 ≥ 4
≥ 4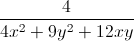 +
+ 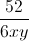 = 16
= 16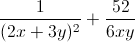 ≥ 16.
≥ 16.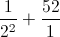 = 56
= 56
Dấu “ = “ xảy ra ⇔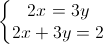 ⇔
⇔ 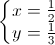
Vậy giá trị nhỏ nhất của biểu thức A là 56.

Gọi số trận đấu mà anh Nam chơi ngày thứ nhất, thứ 2, ..., ngày thứ 20 lần lược là: a1; a2; ...; a n.
Xét 20 tổng :
S1 = a1
S2 = a1 + a2
...................
S n = a1 + a2 + ... + a n
Ta có: S1 < S2 < .... < S n < 36 (vì trong 20 ngày anh Nam không chơi quá 12.3 = 36 trận)
Ta biết rằng 1 số tự nhiên bất kỳ khi chia cho 20 thì có 19 số dư khác 0 là: 1, 2,...,19.
Giờ quay lại bài toán ta thấy
Nếu trong 20 tổng này có 1 tổng chia hết 20 thì bài toán đã được chứng minh (vì các tổng đó lớn hơn 0 nhỏ hơn 36 nên tổng chỉ có thể là 20).
Còn nếu trong 20 tổng này không có tổng nào chia hết cho 20 thì sẽ tồn tại ít nhất 2 tổng có cùng số dư khi chia cho 20.
Giả sử hai tổng đó là S m, S n (m > n) thì ta có S m - S n = (a1 + a2 + ... + a m) - (a1 + a2 + ... + a n) = a n+1 + a n+2 + ...+ a m chia hết cho 20. Hay S m - S n = 20.
Vậy tồn tại một số ngày liên tiếp trong đó anh chơi đúng 20 trận.
.png)
.png)
TH1: "Hòa đạt giải đồng" là đúng.
Tức là "Hoàng không đạt giải đồng" là sai nên Hoàng đạt giải đồng, khi đó Hòa và Hoàng đều đạt giải đồng, mâu thuẫn.
TH2: "Hoàng không đạt giải đồng" là đúng.
Khi đó Hoàng đạt giải vàng hoặc bạc, "Huy đạt giải đồng" là sai nên Huy đạt giải vàng hoặc bạc, khi đó Huy đạt giải đồng.
Khi đó câu "Huy không đạt giải bạc" là đúng, mâu thuẫn.
TH3: "Huy không đạt giải bạc" là đúng.
Huy đạt giải vàng hoặc đồng. "Hoàng không đạt giải đồng" là sai nên Hoàng đạt giải đồng, suy ra Huy đạt giải vàng.
Khi đó Hòa đạt giải bạc.
Chọn B.