nối M với h, ta có: 
MH = AC/2 = MC ( trung tuyến = 1/2 cạnh huyền của tam giác vuông AHC) 
=> MHC^ = MCH^ = 2.KCH^ ( vì CK là phân giác của ACB^) 
gt: KB = KC => KCH^ = KBH^ 
=> MHC^ = 2.KBH^ = KBH^ + KBH^ (1) 
mắt khác: 
MHC^ = KBH^ + KMH^ (2) ( góc ngoài và trong của tam giác BMH) 
(1) và (2) => KBH^ = KMH^ => BHM cân tại H => HB = HM (1) 
tổng góc trong của tam giác BMH là: 
KBH^ + BHA^ + AHM^ + KMH^ = 180* 
=> 2.KBH^ + 90* + AHM^ = 180* 
=> 2.KBH^ + AHM^ = 90* (2) 
tam giác AHC vuông => MAH^ + MCH^ = 90* 
=> MAH^ + 2.KCH^ = 90* 
=> MAH^ + 2.KBH^ = 90* (3) ( vì KCH^ = KBH^) 
(2) và (3) => AHM^ = MAH^ => HA = HM 
mặt khác: HM = AC/2 = AM 
=> HA = HM = AM => AHM là tam giác đều => HA = HM (4) 
(1) và (4) => HA = HB 
=> AHM là tam giác đều => MAH^ = 60* => ACB^ = 30* 
=> ABC^ = 180* - BAC^ - ACB^ = 180* - 105* - 30* = 45* 
(hoặc ABC^ = ABH^ = 45* => ACB^ = 30*)

Vẽ nháp bằng tay, hình không đẹp cho lắm :v Bài viết có hơi lỗi.

Bài toán phụ : Chứng minh tam giác vuông có 1 góc 60 độ thì cạnh góc vuông nhỏ hơn sẽ bằng 1 nửa cạnh huyền.

Tam giác MNP vuông tại M có góc N là 60 độ.

Trên tia đối tia MN lấy điểm Q sao cho MQ=MN

Tam giác NPQ có PM vừa là trung tuyến vừa là đường cao nên cân tại P, mà lại có 1 góc 60 độ nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều), từ đó suy ra NQ = NP, mà NQ= 2MN nên MN = \(\frac{1}{2}\)NP, bài toán được chứng minh.

Tương tự với bài toán của chúng ta :

\(\Delta ABC\)vuông tại Acó \(\widehat{B}=60^o\) \(\Rightarrow AB=\frac{1}{2}BC\)

\(\Delta ABH\)vuông tại H có \(\widehat{B}=60^o\) \(\Rightarrow HB=\frac{1}{2}AB\)

\(\Rightarrow HB=\frac{1}{4}BC\)

Trước hết \(\Delta ABH\) vuông tại H có \(\widehat{B}=60^o\)

 nên \(\widehat{HAB}=90^o-60^o=30^o\)Mà \(\widehat{DAH}+\widehat{HAB}=\widehat{BAC}=90^o\)

\(\Rightarrow\widehat{DAH}=60^o\)

\(\Delta DAH\)cân tại A ( AD = AH ), có góc DAH là 60^o nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều )

Như vậy AI là đường cao đồng thời cũng là phân giác góc DAH

\(\Rightarrow\widehat{IAH}=\frac{1}{2}\widehat{DAH}=\frac{60^o}{2}=30^o\)

\(\Rightarrow\widehat{KAB}=\widehat{IAH}+\widehat{HAB}=30^o+30^o=60^o\)

\(\Delta KAB\)có \(\widehat{KAB}=\widehat{KBA}=60^o\) nên là tam giác đều

\(\Rightarrow KB=AB\)

Mà \(HB=\frac{1}{2}AB\Rightarrow HB=\frac{1}{2}KB\), hay H là trung điểm của KB.

Vậy ....

dung roi

Với mọi đa thức f(x),khi khai triển luôn có dạng : a_n.xⁿ + a_{n - 1}.x^{n - 1} + a_{n - 2}.x^{n - 2} + ... + a₂.x² + a₁.x + a₀

\(\Rightarrow f\left(1\right)=a_n+a_{n-1}+a_{n-2}+...+a_2+a_1+a_0\)là tổng các hệ số của f(x)

Đặt đa thức đã cho là f(x) thì tổng các hệ số của f(x) khi bỏ dấu ngoặc trong biểu thức (khai triển) là :

f(1) = (3 - 4 + 1)²⁰⁰⁶.(3 + 4 + 1)²⁰⁰⁷ = 0²⁰⁰⁶.7²⁰⁰⁷ = 0

Để làm được bài này bạn phải đặt x=1 là tính tổng được hệ só nhé bạn

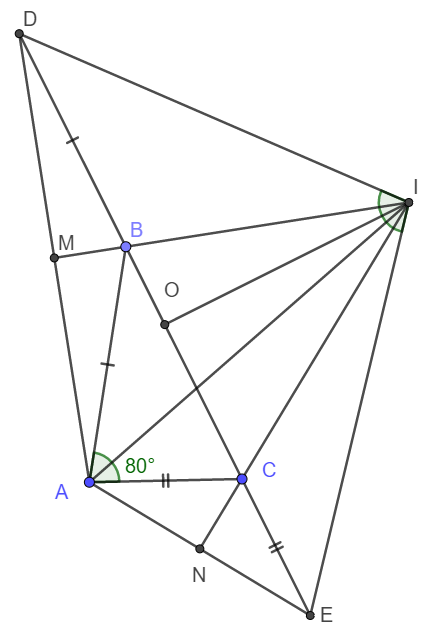
a) Ta có MD = MA; BD  BA nên MB là trung trức của AD.

Vậy nên I thuộc trung trực AD hay ID = IA.

Tương tự IE = IA.

Suy ra ID = IE hay tam giác IDE là tam giác cân tại I.

Lại có IO là trung tuyến nên OI là đường cao hay \(IO\perp DE\) 

b) Ta có \(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{BAC}=180^o-80^o=100^o\)

\(\Rightarrow\widehat{ADB}+\widehat{AFC}=\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}=\frac{100^o}{2}=50^o\)

\(\Rightarrow\widehat{DAB}+\widehat{EAC}=50^o\)

\(\Rightarrow\widehat{DAE}=80^o+50^o=130^o\)

Ta thấy \(\widehat{IDA}=\widehat{IAD};\widehat{IEA}=\widehat{IAE}\Rightarrow\widehat{IDA}+\widehat{IAE}=\widehat{IAD}+\widehat{IEA}=\widehat{DAE}=130^o\)

\(\Rightarrow\widehat{DIE}=360^o-130^o-130^o=100^o\)

Ta thấy ngay \(\widehat{MIN}=\widehat{MIA}+\widehat{NIA}=\frac{\widehat{DIA}}{2}+\frac{\widehat{EIA}}{2}=\frac{100^o}{2}=50^o\)

Bài bạn đấy nhìn khó hiểu???

khi đó tổng này sẽ phụ thuộc vào hiệu 2 ẩn nào đó, tuỳ theo mỗi trường hợp

thử chia đi, mình đúng cho ,mình mọt sách

Ta có: \(AC-AB>CK-BH\)    (*)

\(\Leftrightarrow AC+BH>AB+CK\)

\(\Leftrightarrow\left(AC+BH\right)^2>\left(AB+CK\right)^2\)

\(\Leftrightarrow AC^2+BH^2+2.AC.BH>AB^2+CK^2+2.AB.CK\)

\(\Leftrightarrow AC^2+BH^2+4S_{ABC}>AB^2+CK^2+4S_{ABC}\)

\(\Leftrightarrow AC^2+BH^2>AB^2+CK^2\)

\(\Leftrightarrow AK>AH\)  (**)

Xét tam giác ABC có \(\widehat{B}>\widehat{C}\Rightarrow AC>AB\)

Trên AC lấy điểm B' sao cho AB' = AB \(\Rightarrow AB'< AC\Rightarrow\) B' nằm giữa A và C.  (1)

Kẻ B'K' vuông góc AB tại K'.Suy ra B'K' // KC   (2)

Từ (1) và (2) suy ra K' nằm giữa A và K hay AK' < AK

Ta thấy ngay \(\Delta ABH=\Delta ACK'\)  (Cạnh huyền - góc nhọn) 

\(\Rightarrow AH=AK'\Rightarrow AK>AH\)

Vậy (**) đúng hay (*) đúng.

Ta có tam giác AKC vuông tại K

=> AC là cạnh lớn nhất (nhận xét quan hệ giữa cạnh đối diện với góc lớn hơn)

=>AC > CK

Ta có tam giác ABH vuông tại H

=> AB là cạnh lớn nhất (nhận xét quan hệ giữa cạnh đối diện với góc lớn hơn)

=> AB > BH

 Có: AC>CK;

AB>BH (cmt)

=> AC-AB > CK-BH

Ta có:

\(\frac{a_1}{a_2}=\frac{a_2}{a_3};\frac{a_2}{a_3}=\frac{a_3}{a_4};...;\frac{a_{2015}}{a_{2016}}=\frac{a_{2016}}{a_{2017}}\)

\(\Rightarrow\frac{a_1}{a_2}=\frac{a_2}{a_3}=...=\frac{a_{2016}}{a_{2017}}=k\)

\(\Rightarrow\frac{a_1^{2016}}{a_2^{2016}}=\frac{a_2^{2016}}{a_3^{2016}}=...=\frac{a_{2016}^{2016}}{a_{2017}^{2016}}=\frac{a_1^{2016}+a_2^{2016}+...+a_{2016}^{2016}}{a_2^{2016}+a_3^{2016}+...+a_{2017}^{2016}}=k^{2016}\left(1\right)\)

Ta lại có: 

\(k^{2016}=\frac{a_1}{a_2}.\frac{a_2}{a_3}...\frac{a_{2016}}{a_{2017}}=\frac{a_1}{a_{2017}}\left(2\right)\)

Từ (1) và (2) \(\frac{a_1^{2016}+a_2^{2016}+...+a_{2016}^{2016}}{a_2^{2016}+a_3^{2016}+...+a_{2017}^{2016}}=\frac{a_1}{a_{2017}}\)

Ta kéo dài tia MA , lấy điểm N thuộc tia MA sao cho IN = IK

Dễ thấy OAMB là hình vuông vì có góc O = góc B = góc A = 90⁰ và OM là tia phân giác góc O . => OA = OB

Ta có :  IN = IK (dựng hình) ; \(\widehat{NIO}=\widehat{OIK}\) (gt) ; IO là cạnh chung của hai tam giác NIO và OIK

=> \(\Delta NIO=\Delta IOK\left(c.g.c\right)\)=> \(\widehat{NOI}=\widehat{IOK}\) ; ON = OK

Xét hai tam giác vuông : \(\Delta AON\) và \(\Delta BOK\)có  OA = OB (cmt) ; ON = OK (cmt)  

=> \(\Delta AON=\Delta BOK\left(ch.cgv\right)\) => \(\widehat{AON}=\widehat{BOK}\)

Mà \(\widehat{BOK}+\widehat{AOK}=90^o\) \(\Rightarrow\widehat{AON}+\widehat{AOK}=90^o\)

hay \(\widehat{NOK}=2\widehat{IOK}=90^o\Rightarrow\widehat{IOK}=\frac{90^o}{2}=45^o\)

Cô ghi dấu góc ở đâu vậy

mình cũng ko chắc lắm nhé bạn

Ta đặt số cây của các tổ là A
ta có:
Số cây tổ 1 là 20 + ( A - 20 ) 0,04
Số cây tổ 2 là 21 + ( A - 21 - 20 - ( A - 20 ) 0,04 ) 0,04
Ta có số cây mỗi tổ bằng nhau
=> 20 +( A - 20 ) 0,04 = 21 + ( A - 21 - 20 - ( A - 20 ) 0,04 ) 0,04
<=> 20+ 0,04A - 0,8 = 21 + ( 0,96A - 40,2 ) 0,04
<=> 0.04A + 19,2 = 21 + 0,0384A - 1,608
<=> 1/625A = 0,192
<=> A = 120
Ta sẽ có số cây tổ 1 là  20 + ( 120 - 20 ) 0,04 = 24 cây
vì số cây mỗi tổ bằng nhau nên số cây mỗi tổ là 120 : 24 = 5 (tổ)
Vậy số cây mỗi tổ là 24 cây
Lớp 7a có 5 tổ

Ta có:

\(y^3=\left(x-2\right)^4-x^4\)

\(\Leftrightarrow y^3=-8\left(x-1\right)\left(x^2-2x+2\right)\)

\(\Rightarrow\)y là số chẵn

Đặt \(y=-2k\left(k\in Z\right)\)

\(\Rightarrow-8k^3=-8\left(x-1\right)\left(x^2-2x+2\right)\)

\(\Leftrightarrow k^3=\left(x-1\right)\left(x^2-2x+2\right)\)

Đễ dàng chứng minh được \(\left(x-1\right);\left(x^2-2x+2\right)\) nguyên tố cùng nhau

\(\Rightarrow\hept{\begin{cases}x-1=m^3\\x^2-2x+2=n^3\end{cases}}\)

\(\Rightarrow n^3=m^6+1\)

Ta lại có: \(m^6< m^6+1\le\left(m^2+1\right)^3\)

\(\Rightarrow m^6+1=\left(m^2+1\right)^3\)

\(\Leftrightarrow m^2\left(m^2+1\right)=0\)

\(\Leftrightarrow m=0\)

\(\Rightarrow\hept{\begin{cases}x=1\\y=0\end{cases}}\)