(2 điểm) Dựng ảnh và nêu đặc điểm của ảnh của một vật tạo bởi thấu kính hội tụ trong các trường hợp sau:
a. Khoảng cách từ vật đến thấu kính lớn hơn tiêu cự của thấu kính (d > f)
b.. Khoảng cách từ vật đến thấu kính nhỏ hơn tiêu cự của thấu kính (d < f).

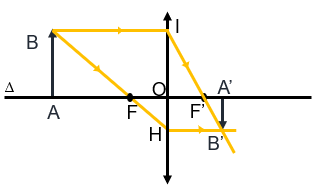


a. Khoảng cách từ vật đến thấu kính lớn hơn tiêu cự của thấu kính (d > f)
Khi vật đặt ngoài khoảng tiêu cự, ảnh thật ngược chiều với vật.
b.. Khoảng cách từ vật đến thấu kính nhỏ hơn tiêu cự của thấu kính (d < f).
Khi vật đặt trong khoảng tiêu cự, ảnh ảo cùng chiều với vật và lớn hơn vật.
00000000