có phải bạn học đội tuyển toán 6 đúng không

Để  pq+17 >2 là số nguyên tố thì pq là số chẵn 

=> p chia hết 2 hoặc q chia hết 2

Vì p, q là số nguyên tố nên có 2 trường hợp xảy ra:

TH1: p=2 

=> 7.p+q=7.2+q=14+q 

q là số nguyên tố 

+) q=3 

Ta có: 7x2+3=17 là số nguyên tố

2x3+17=23 là số nguyên tố

=> q=3 thỏa mãn

+) q chia 3 dư 1 => q=3k+1 (k thuộc N)

7p+q=14+3k+1=15+3k chia hết cho 3 không phải là số nguyên tố

nên trường hợp này loại

+) q chia 3 dư 2 => q=3k+2 ( k thuộc N)

pq+17=(3k+2).2+17=6k+21 chia hết cho 3 không phải là số nguyên tố

nên trường hợp này cũng bị loại

Vậy p=2, q=3 là thỏa mãn

TH2: q=2

Ta có: 7p+q=7p+2

    pq+17=2p+17

Vì: p là số nguyên tố  ta có các trường hợp nhỏ sau:

+) Với  p=3

=> 7p+2=23 là số nguyên tố

2p+17=23 là số nguyên tố

=> p =3 thỏa mãn

+) Với p chia 3 dư 1 => p=3k+1 ( k thuộc N)

7p+2=7(3k+1)+2=21k+9 chia hết cho 3 nên không phải là số nguyên tố nên  loại 

+Với p chia 3 dư 2 => p=3k+2 

2p+17=2(3k+2)+17=6k+21 chia hết cho 3 nên không phải là số nguyên tố nên loại

Vậy q=2, p=3 là thỏa mãn

Kết luận cả 2 TH: p=2, q=3 hoawch q=2, p=3

gọi 6 số tn lần lượt là :a;b;c;d;e;f

tổng 6 số trên là : a+b+c+d+e+f= 60

trung bình cộng của 5 số cuối =11=>b+c+d+e+f=55=>a=60-55=5

__________________số đầu=9=>a+b+c+d+e=45+=>f=60-45=15

thay a=5, f=15 vào : a+b+c+d+e+f=60 , ta có: 5+b+c+d+e+15=60

                                                                    =>b+c+d+e     =60-5-15=40

trung bình cộng của : a+b+c+d+e= 40:4=10

Vậy trung bình cộng của 4 số ở giữa là 10

gọi 6 số tn lần lượt là :a;b;c;d;e;f

tổng 6 số trên là : a+b+c+d+e+f= 60

trung bình cộng của 5 số cuối =11=>b+c+d+e+f=55=>a=60-55=5

__________________số đầu=9=>a+b+c+d+e=45+=>f=60-45=15

thay a=5, f=15 vào : a+b+c+d+e+f=60 , ta có: 5+b+c+d+e+15=60

                                                                    =>b+c+d+e     =60-5-15=40

trung bình cộng của : a+b+c+d+e= 40:4=10

Vậy trung bình cộng của 4 số ở giữa là 10

a) CD//Ey

=> ^CBE = ^BEy = 130^o

b) Ta có ^xAB + ^ABD = 180^o 

=>Ax // CD

Mà CD // Ey 

=> Ax//Ey

C.

Có CD//Ey (giả thiết)

=>^DBE+^BEy=180 (hai góc ở vị trí trong cùng phí

=>^DBE=180-^BEy=180-130=50

Có ^ABD+^DBE=40+50=90

=>^ABE=90

=>AB vuông góc BE (ĐPCM)

Em viết phần intro nha:

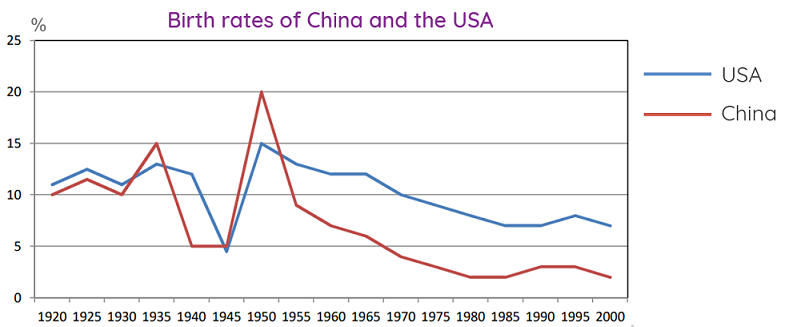
The chart above decsribes how the birth rates of 2 countries namely China, USA changed in 80 years which started from 1920

Answer:
The line graph compares the birth rates in China and the US and how these rates changed from 1920 to 2000.
Overall, there was a general decline in fertility of both nations throughout the time surveyed. However, the US’s birth rates almost was higher than that of China over the whole period.
American saw a significant fluctuation in the birth rates between 1920 to 1935, but it always remained over 10%. However, in the following decade, the fertility of the US decreased sharply to under 5 %. From 1945 to 1950, there was a rapidly increased in American’s birth rates, at 15%, reaching the highest point of it’s own during the whole period. From that on, the fertility of the US fell gradually to 7% in 2000.
During the 80-year period, the birth rates in China changed more significantly than in the US. It fell down to 5% in the year 1940, then reaching a peak of whole line graph in 1950, at 20%. Over the remainder of the period, China saw a sharply drop in the birth rates to only about 2% until 2000.

Nhận thấy n=2 thỏa mãn điều kiện

Với n>2 ta có: 

\(n^6-1=\left(n^3-1\right)\left(n^3+1\right)=\left(n^3-1\right)\left(n+1\right)\left(n^2-n+1\right)\)

Do đó tất cả các thừa số nguyên tố của \(n^2-n-1\)chia hết cho \(n^3-1\)hoặc \(n^2-1=\left(n-1\right)\left(n+1\right)\)

Để ý rằng \(\left(n^2-n+1;n^3-1\right)\le\left(n^3+1;n^3-1\right)\le2\)

Mặt khác \(n^2-n+1=n\left(n-1\right)+1\)là số lẻ, do đó tất cả các thừa số nguyên tố của \(n^2-n-1\)chia hết cho \(n+1\)

Nhưng \(n^2-n+1=\left(n+1\right)\left(n-2\right)+3\)

Vì vậy ta phải có \(n^2-n+1=3^k\left(k\in Z^+\right)\)

Vì \(n>2\Rightarrow k\ge2\)

do đó \(3|n^2-n+1\Rightarrow n\equiv2\left(mod3\right)\)

Nhưng mỗi TH \(n\equiv2,5,8\left(mod9\right)\Rightarrow n^2-n+1\equiv3\left(mod9\right)\)(mâu thuẫn)

Vậy n=2

Bài làm rất hay mặc dù làm rất tắt.

Tuy nhiên:

Dòng thứ 4: Ước số nguyên tố của \(n^2-n+1\)chia hết cho \(n^3-1\)hoặc \(n^2-1\)( em viết thế này không đúng rồi )

------> Sửa: ước số nguyên tố của \(n^2-n+1\) chia hết \(n^3-1\) hoặc  \(n^2-1\)

Hoặc:  ước số nguyên tố của \(n^2-n+1\) là ước  \(n^3-1\) hoặc  \(n^2-1\)

Dòng thứ 6 cũng như vậy:

a chia hết b khác hoàn toàn a chia hết cho b 

a chia hết b nghĩa là a là ước của b ( a |b)

a chia hết cho b nghĩa là b là ước của a.( \(a⋮b\))

3 dòng cuối cô không hiểu  em giải thích rõ giúp cô với. Please!!!!

Nhưng cô có cách khác dễ hiểu hơn này:

\(n^2-n+1=3^k\);

 \(n+1⋮3\)=> tồn tại m để : n + 1 = 3m

=> \(\left(n+1\right)\left(n-2\right)+3=3^k\)

<=>\(3m\left(n+1-3\right)+3=3^k\)

<=> \(m\left(n+1\right)-3m+1=3^{k-1}\)

=> \(m\left(n+1\right)-3m+1⋮3\)

=> \(1⋮3\)vô lí

a)106:6+101:6

=(106+101):6

=207:6

=34,5

b)100:9-79,3:9

=(100-79,3):9

=20,7:9

=2,3

Cảm ơn bạn

Gọi ba số đó là \(a,b,c\)(\(a,b,c\inℕ^∗\))

\(a+b+c=100\)

\(P=abc\).

Dễ thấy GTNN của \(P\)đạt tại hai số bằng \(1\), một số bằng \(98\).

\(minP=98\)khi \(\left(a,b,c\right)=\left(1,1,98\right)\)và các hoán vị. 

Giờ ta sẽ tìm GTLN của \(P\).

Giả sử \(a\ge b\ge c\).

Ta có nhận xét rằng \(P\)đặt giá trị lớn nhất khi hai trong ba số trên có hiệu không vượt quá \(1\).

Giả sử \(a-b>1\).

Khi đó thay \(a\)bởi \(a-1\), \(b\)bởi \(b+1\)ta có: 

\(c\left(a-1\right)\left(b+1\right)=c\left(ab+a-b-1\right)>cab\)

Do đó \(P\)đạt GTLN khi \(a\ge b\ge c\), \(a-c\le1\). 

Kết hợp với \(a+b+c=100\)suy ra \(P\)đạt max tại \(a=34,b=c=33\).

Khi đó \(maxP=34.33^2\).

Dấu \(=\)khi \(\left(a,b,c\right)=\left(34,33,33\right)\)và các hoán vị. 

(34,33,33) và các hoán vị

gọi 3 số đó là a,b,c

a+b+c=100

theo bdt cosi: a+b+c>=\(3\sqrt[3]{abc}\)

\(\Leftrightarrow100\ge3\sqrt[3]{abc}\Leftrightarrow\frac{1000000}{27}\ge abc\)

vậy abc đạt gtln là 1000000/27 hay tích 3 số đó có GTLN là 1000000/27

B1:

1. She doesn't sleep late on weekends

2. We don't believe in ghost

3. Do you understand the question?

4. They don't work late on Friday

5. Does David want some coffee?

6. She has three daughters

7. When does she go to her Chinese class?

8. Why do I have to clean up?

B2:

1, has

2, is

3. is

4. lik.es

5. never bites

6. barks

7. is

8. doesn't li.ke

9. often plays

10. becomes

11. just sleeps

12. plays

13. are

14. doesn't let

15. often takes

16. sometimes is

Bài 1

1. She doesn't sleep late on weekends

2. We don't believe in ghost

3. Do you understand the question ?

4. They do not work late on Friday

5. Does David want some coffee ?

6. She has three daughters

7. When does she go to her Chinese class ?

8. Why do I have to clean up ?