Cho a,b,c >0 thỏa \(2ab+6bc+2ca=7abc\).Tìm GTNN của
\(C=\frac{4ab}{a+2b}+\frac{9ac}{4c+a}+\frac{4bc}{b+c}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(H=\frac{xz}{y^2+yz}+\frac{y^2}{zx+yz}+\frac{x+2z}{x+z}\)
\(=\frac{1}{\frac{y^2}{xz}+\frac{yz}{xz}}+\frac{1}{\frac{zx}{y^2}+\frac{yz}{y^2}}+\frac{x+z+z}{x+z}\)
\(=\frac{1}{\frac{y^2}{zx}+\frac{y}{x}}+\frac{1}{\frac{zx}{y^2}+\frac{z}{y}}+\frac{1}{\frac{x}{z}+1}+1\)
Đặt \(\frac{x}{y}=a;\frac{y}{z}=b\Rightarrow ab=\frac{x}{z}\ge1\)
Khi đó \(H=\frac{1}{\frac{b}{a}+\frac{1}{a}}+\frac{1}{\frac{a}{b}+\frac{1}{b}}+\frac{1}{ab+1}+1\)
\(=\frac{a}{b+1}+\frac{b}{a+b}+\frac{1}{ab+1}+1\)
Ta cần chứng minh \(U=\frac{a}{b+c}+\frac{b}{a+b}+\frac{1}{ab+1}\ge\frac{3}{2}\)
\(\Leftrightarrow\left(\frac{a}{b+1}+1\right)+\left(\frac{b}{a+1}+1\right)+\frac{1}{ab+1}\ge\frac{7}{2}\)
\(\Leftrightarrow\frac{a+b+1}{b+1}+\frac{a+b+1}{a+1}+\frac{1}{ab+1}\ge\frac{7}{2}\)
\(\Leftrightarrow\left(a+b+1\right)\left(\frac{1}{b+1}+\frac{1}{a+1}\right)+\frac{1}{ab+1}\ge\frac{7}{2}\)
Khi đó \(Y=\left(a+b+1\right)\left(\frac{1}{a+1}+\frac{1}{b+1}\right)+\frac{1}{ab+1}\)
\(\ge\left(a+b+1\right)\cdot\frac{4}{a+b+2}+\frac{1}{ab+1}\)
\(\ge\frac{4\left(a+b+1\right)}{a+b+2}+\frac{1}{\frac{\left(a+b\right)^2}{4}+1}\)
Đặt \(t=a+b\ge2\sqrt{ab}\ge2\)
Ta cần chứng minh \(\frac{4\left(t+1\right)}{t+2}+\frac{1}{\frac{t^2}{4}+1}\ge\frac{7}{2}\)
\(\Leftrightarrow\frac{\left(t-2\right)^3}{2\left(t+2\right)\left(t^2+4\right)}\ge0\) ( đúng )
Vậy ta có đpcm.
ta có:
\(\frac{xz}{y^2+yz}+\frac{y^2}{xz+yz}+\frac{z+2z}{z+x}=\frac{\frac{xz}{yz}}{\frac{y^2}{yz}+1}+\frac{\frac{y^2}{yz}}{\frac{xz}{yz}+1}+\frac{1+\frac{2z}{x}}{1+\frac{z}{x}}\)\(=\frac{\frac{x}{y}}{\frac{y}{z}+1}+\frac{\frac{y}{z}}{\frac{x}{y}+1}+\frac{1+\frac{2z}{x}}{1+\frac{z}{x}}=\frac{a^2}{b^2+1}+\frac{b^2}{a^2+1}+\frac{1+2c^2}{1+c^2}\)
trong đó \(a^2=\frac{x}{y};b^2=\frac{y}{z};c^2=\frac{z}{x}\left(a;b;c>0\right)\)
Nhận xét rằng \(a^2\cdot b^2=\frac{x}{z}=\frac{1}{c^2}\ge1\)(do x>=z)
Xét \(\frac{a^2}{b^2+1}+\frac{b^2}{a^2+1}+\frac{c^2}{ab+1}\)\(=\frac{a^2\left(a^2+1\right)\left(ab+1\right)+b^2\left(b^2+1\right)\left(ab+1\right)-2aba^2\left(a^2+1\right)\left(b^2+1\right)}{\left(a^2+1\right)\left(b^2+1\right)\left(ab+1\right)}\)
\(=\frac{ab\left(a^2-b^2\right)+\left(a-b\right)\left(a^3-b^3\right)+\left(a-b\right)^2}{\left(a^2+1\right)\left(b^2+1\right)\left(ab+1\right)}\ge0\)
Do đó: \(\frac{a^2}{b^2+1}+\frac{b^2}{a^2+1}\ge\frac{2ab}{ab+1}=\frac{\frac{2}{c}}{\frac{1}{c}+1}=\frac{2}{1+c}\left(1\right)\)đẳng thức xảy ra <=> a=b
khi đó:
\(\frac{2}{1+c}+\frac{1+2c^2}{c^2+1}-\frac{5}{2}=\frac{2\left[2\left(1+c^2\right)+\left(1+c\right)\left(1+2c^2\right)\right]-5\left(1+c\right)\left(1+c^2\right)}{2\left(1+c\right)\left(1+c^2\right)}\)
\(=\frac{1-3c+3c^2-c^3}{2\left(1+c\right)\left(1+c^2\right)}=\frac{\left(1-c\right)^3}{2\left(1+c\right)\left(1+c^2\right)}\ge0\)(do c=<1) (2)
Từ (1) và (2) => đpcm
Đẳng thức xảy ra <=> a=b, c=1 <=> x=y=z

\(\hept{\begin{cases}\frac{7}{2}+\frac{3y}{x+y}=\sqrt{x}+4\sqrt{y}\left(1\right)\\\left(x^2+y^2\right)\left(x+1\right)=4+2xy\left(x-1\right)\left(2\right)\end{cases}}\)
ĐK: x>=0; y>=0 và x+y\(\ne\)0 (*)
Ta có (2) <=> \(x^3-2x^2y+xy^2+x^2+y^2+2xy=4\)
\(\Leftrightarrow x\left(x-y\right)^2+\left(x+y\right)^2=4\)
Từ điều kiện (*) => x(x-y)2 >=0; x+y>0
Do đó: (x+y)2 =< 4 => 0<x+y =< 2
Từ đó suy ra: \(\frac{7}{2}+\frac{3y}{x+y}\ge\frac{7+3y}{2}\left(3\right)\)
Áp dụng BĐT Cauchy với 2 số không âm ta có:
\(\sqrt{x}\le\frac{x+1}{2};4\sqrt{y}\le2\left(y+1\right)\)
Cộng 2 vế BĐT trên ta có:
\(\sqrt{x}+4\sqrt{y}\le\frac{x+1}{2}+2\left(y+1\right)=\frac{\left(x+y\right)+5+3y}{2}\le\frac{7+3y}{2}\left(4\right)\)
Từ (3) và (4) => \(\sqrt{x}+4\sqrt{y}\le\frac{7}{2}+\frac{3y}{x+y}\)
Kết hợp với (1) thì đẳng thức xảy ra tức là:
\(\hept{\begin{cases}x+y=2\\x=1\\y=1\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}}\)(tmđk (*))
Vậy hệ phương trình có nghiệm duy nhất \(\hept{\begin{cases}x=1\\y=1\end{cases}}\)

\(=\)\(18\left(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}\right)\)\(=\)\(18\frac{3}{1}\)\(>\)\(\left(9+5\sqrt{3}\right)\left(a^2+b^2+c^2\right)\)\(=\)\(0\)
Vậy\(18\frac{3}{1}\)\(>\)\(0\)
Chứng minh là \(18\frac{3}{1}\)\(>\)\(0\)là đúng
chúc bạn học tốt
Bất đẳng thức trên
<=> 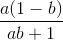 + 1 +
+ 1 + 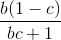 + 1 +
+ 1 + 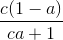 + 1 ≥ 3
+ 1 ≥ 3
<=> 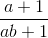 +
+ 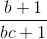 +
+ 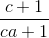 ≥ 3 (*)
≥ 3 (*)
Ta có: VT(*) ≥ 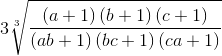
Ta sẽ chứng minh: (a + 1)(b + 1)(c + 1) ≥ (ab + 1)(bc + 1)(ca + 1)
<=> abc + ab + bc + ca + a + b + c + 1
≥ a2b2c2 + abc(a + b + c) + ab + bc + ca + 1
<=> 3 ≥ a2b2c2 + 2abc (**)
Theo Cosi: 3 = a + b + c ≥ 3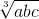 =>
=> 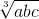 ≤ 1 => abc ≤ 1
≤ 1 => abc ≤ 1
Vậy (**) đúng => (*) đúng.

Chắc khó nhất ở chỗ: khử abc
Theo dirichlet
a(b-1)(c-1) \(\ge0\)
=> abc \(\ge\)ab + ac - a
Thay vào ta có: \(25\left(a^2+b^2+c^2\right)+54abc+36\ge25\left(a^2+b^2+c^2\right)+54\left(ab+bc-a\right)^2+36\)
Ta cần chứng minh:
\(25\left(a^2+b^2+c^2\right)+54\left(ab+ac-a\right)+36\ge6\left(a+b+c\right)+49\left(ab+bc+ac\right)\) (1)
Đến đây thì có thể dùng nhiều cách: Vì mình cũng dễ thấy nghiệm có a = b = c = 1
Dùng trung bình nhân ( hoặc cách khác)
SOS forever!
VT - VP
\(=\frac{\left(54bc+50a-49b-49c-6\right)^2}{100}-\frac{9\left(54bc+b-49c-6\right)^2\left(6c-11\right)}{5400c+100}+\frac{1350c\left(c-1\right)^2}{54c+1}\)
\(=\frac{\left(50a+50b-49c-6\right)^2}{100}+\frac{99\left(c-6\right)^2}{100}+9ab\left(6c-11\right)\)
Từ 2 đẳng thức trên có đpcm. Nếu muốn thì em gộp lại thành 1 biểu thức SOS giống a cho đẹp :D Tại hôm nay làm biếng nên viết tách ra, gộp mất công dò lại nhiều:v

\(\Leftrightarrow\left(\Sigma a\right)^4\left(\Sigma a^4b^4\right)\left[\Sigma c^2\left(a^2+b^2\right)^2\right]\ge54^2\left(abc\right)^6\)
Giả sử \(c=\text{min}\left\{a,b,c\right\}\)và đặt \(a=c+u,b=c+v\) thì nhận được một BĐT hiển nhiên :P
Theo BĐT AM-GM ta có:
\(c^2\left(a^2+b^2\right)^2+a^2\left(b^2+c^2\right)^2+b^2\left(c^2+a^2\right)\ge3\sqrt[3]{\left(abc\right)^2\left[\left(a^2+b^2\right)\left(b^2+c^2\right)\left(c^2+a^2\right)\right]^2}\)
\(\ge3\sqrt[3]{\left(abc\right)^264\left(abc\right)^4}=12\left(abc\right)^2\)
=> \(\sqrt{c^2\left(a^2+b^2\right)^2+a^2\left(b^2+c^2\right)^2+b^2\left(a^2+c^2\right)^2}\ge2\sqrt{3}abc\)
Cũng theo BĐT AM-GM \(\left(ab\right)^4+\left(bc\right)^4+\left(ca\right)^4\ge3\sqrt[3]{\left(ab\right)^4\left(bc\right)^4\left(ca\right)^4}=3\left(abc\right)^2\sqrt[3]{\left(abc\right)^2}\)
=> \(\sqrt{\left(ab\right)^4+\left(bc\right)^4+\left(ca\right)^4}\ge\sqrt{3}\cdot abc\sqrt[3]{abc}\)và \(\left(a+b+c\right)^2\ge9\sqrt[3]{\left(abc\right)^2}\)
=> \(\sqrt{c^2\left(a^2+b^2\right)^2+a^2\left(b^2+c^2\right)^2+b^2\left(c^2+a^2\right)^2}\cdot\left(a+b+c\right)^2\cdot\sqrt{\left(ab\right)^4+\left(bc\right)^4+\left(ca\right)^4}\)
\(\ge2\sqrt{3}\left(abc\right)\cdot\sqrt{3}\left(abc\right)\sqrt[3]{abc}\cdot9\sqrt[3]{\left(abc\right)^2}\ge54\left(abc\right)^3\)
Dấu "=" xảy ra <=> a=b=c

\(\sqrt[3]{\overline{xyz}}=x+y+z\)
\(\Leftrightarrow\overline{xyz}=\left(x+y+z\right)^3\)
Đặt \(m=x+y+z\Rightarrow m\equiv\overline{xyz}\left(mod9\right)\)
\(\Rightarrow\overline{xyz}-m⋮9\)
Đặt \(\overline{xyz}-m=9k\left(k\inℕ\right)\)
\(\Leftrightarrow m^3-m=9k\Leftrightarrow\left(m-1\right)m\left(m+1\right)=9k\)
\(\Rightarrow\left(m-1\right)m\left(m+1\right)⋮9\)
Nhận xét:trong 3 số tự nhiên liên tiếp tồn tại duy nhất 1 số chia hết cho 3 mà tích chúng chia hết cho 9 nên tồn tại duy nhất 1 số chia hết cho 9
Mặt khác \(100\le\overline{xyz}\le999\Rightarrow100\le m^3\le999\)
\(\Leftrightarrow4\le m\le9\Rightarrow3\le m-1\le8;5\le m+1\le10\)
Nếu \(m⋮9\Rightarrow m=9\Rightarrow\overline{xyz}=9^3=729\)
Thử lại ta thấy không thỏa mãn,loại
Nếu \(m-1⋮9\left(KTM\right)\)
Nếu \(m+1⋮9\Rightarrow m+1=9\Rightarrow m=8\Rightarrow\overline{xyz}=8^3=512\)
Thử lại ta thấy thỏa mãn
Vậy số đó là 512

bạn Kiệt có đánh sai chỗ nào ko vậy :)). mình thấy có 1 lỗi :)).
Đặt \(a=2x+y;b=2y+x\) \(\left(a,b>0\right)\)
Khi đó : \(P=\frac{2}{\sqrt{a^3+1}-1}+\frac{2}{\sqrt{b^3+1}-1}+\frac{ab}{4}-\frac{8}{a+b}\)
Cô-si , ta có : \(\sqrt{a^3+1}=\sqrt{\left(a+1\right)\left(a^2-a+1\right)}\le\frac{a+1+a^2-a+1}{2}=\frac{a^2+2}{2}\)
\(\Rightarrow\sqrt{a^3+1}-1\le\frac{a^2}{2}\)
Tương tự : \(\sqrt{b^3+1}-1\le\frac{b^2}{2}\)
Mặt khác : \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\Rightarrow\frac{2}{a}+\frac{2}{b}\ge\frac{8}{a+b}\Rightarrow-\frac{8}{a+b}\ge\frac{-2}{a}-\frac{2}{b}\)
\(P\ge\frac{4}{a^2}+\frac{4}{b^2}+\frac{ab}{4}-\frac{2}{a}-\frac{2}{b}=\left(\frac{4}{a^2}+1\right)+\left(\frac{4}{b^2}+1\right)+\frac{ab}{4}-\frac{2}{a}-\frac{2}{b}-2\)
\(\ge\frac{4}{a}+\frac{4}{b}+\frac{ab}{4}-\frac{2}{a}-\frac{2}{b}-2=\frac{2}{a}+\frac{2}{b}+\frac{ab}{4}-2\ge3\sqrt[3]{\frac{2}{a}.\frac{2}{b}.\frac{ab}{4}}-2=1\)
Vậy GTNN của P là 1 \(\Leftrightarrow a=b=2\Leftrightarrow x=y=\frac{2}{3}\)
Mình nghĩ đề sửa là:
Cho các số x,y nguyên. Tìm GTM của biểu thức
\(P=\frac{2}{\sqrt{\left(2x+y\right)^3+1}-1}+\frac{2}{\sqrt{\left(x+2y\right)^3+1}-1}+\frac{\left(2x+y\right)\left(x+2y\right)}{4}-\frac{8}{3\left(x+y\right)}\)
Cách làm giống @Thanh Tùng DZ@ nên không trình bày lại

Ta có \(P=\frac{x\left(yz+1\right)^2}{z^2\left(zx+1\right)}+\frac{y\left(zx+1\right)^2}{x^2\left(xy+1\right)}+\frac{z\left(xy+1\right)^2}{y^2\left(yz+1\right)}\)
\(=\frac{\frac{\left(yz+1\right)^2}{z^2}}{\frac{zx+1}{x}}+\frac{\frac{\left(zx+1\right)^2}{x^2}}{\frac{xy+1}{y}}+\frac{\frac{\left(xy+1\right)^2}{y^2}}{\frac{yz+1}{z}}\)
\(=\frac{\left(y+\frac{1}{z}\right)^2}{z+\frac{1}{x}}+\frac{\left(z+\frac{1}{x}\right)^2}{x+\frac{1}{y}}+\frac{\left(x+\frac{1}{y}\right)^2}{y+\frac{1}{z}}\)
Áp dụng BĐT \(\frac{a_1^2}{b_1}+\frac{a_2^2}{b_2}+\frac{a_3^2}{b_3}\ge\frac{\left(a_1+a_2+a_3\right)^2}{b_1+b_2+b_3}\)
Dấu "=" xảy ra khi \(\frac{a_1}{b_1}=\frac{a_2}{b_2}=\frac{a_3}{c_3}\)
\(P=\frac{\left(y+\frac{1}{z}\right)^2}{z+\frac{1}{x}}+\frac{\left(z+\frac{1}{x}\right)^2}{x+\frac{1}{y}}+\frac{\left(x+\frac{1}{y}\right)^2}{y+\frac{1}{z}}\ge\frac{\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2}{\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)}\)
\(P\ge a+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\)
Áp dụng BĐT: \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{9}{x+y+z}\)
=> \(P\ge x+y+z+\frac{9}{x+y+z}=\left[x+y+z+\frac{9}{4\left(x+y+z\right)}\right]+\frac{27}{4\left(x+y+z\right)}\)
Ta có: \(x+y+z+\frac{9}{4\left(x+y+z\right)}\ge2\sqrt{\frac{9}{4}}=3;\frac{27}{4\left(x+y+z\right)}=\frac{27}{4\cdot\frac{3}{2}}=\frac{9}{2}\)
=> \(P\ge3+\frac{9}{2}=\frac{15}{2}\).
Dấu "=" xảy ra <=> x=y=z=\(\frac{1}{2}\)
Vậy MinP=\(\frac{15}{2}\)đạt được khi x=y=z=\(\frac{1}{2}\)
Ta có:
\(P=\frac{x\left(yz+1\right)^2}{z^2\left(zx+1\right)}+\frac{y\left(zx+1\right)^2}{x^2\left(xy+1\right)}+\frac{z\left(xy+1\right)^2}{y^2\left(yz+1\right)}\)
\(=\frac{\left(\frac{yz+1}{z}\right)^2}{\left(\frac{zx+1}{x}\right)}+\frac{\left(\frac{zx+1}{x}\right)^2}{\left(\frac{xy+1}{y}\right)}+\frac{\left(\frac{xy+1}{y}\right)^2}{\left(\frac{yz+1}{z}\right)}\)
\(=\frac{\left(y+\frac{1}{z}\right)^2}{z+\frac{1}{x}}+\frac{\left(z+\frac{1}{x}\right)^2}{x+\frac{1}{y}}+\frac{\left(x+\frac{1}{y}\right)^2}{y+\frac{1}{z}}\)
Áp dụng BĐT Bunhiacopxki dạng phân thức, ta có:
\(\frac{\left(y+\frac{1}{z}\right)^2}{z+\frac{1}{x}}+\frac{\left(z+\frac{1}{x}\right)^2}{x+\frac{1}{y}}+\frac{\left(x+\frac{1}{y}\right)^2}{y+\frac{1}{z}}\)\(\ge\frac{\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2}{x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}=x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\)
\(\ge\left(x+y+z\right)+\frac{9}{x+y+z}=\left(x+y+z\right)+\frac{9}{4\left(x+y+z\right)}\)
\(+\frac{27}{4\left(x+y+z\right)}\ge2\sqrt{\left(x+y+z\right).\frac{9}{4\left(x+y+z\right)}}+\frac{27}{4.\frac{3}{2}}=\frac{15}{2}\)(Áp dụng BĐT Cô - si cho 2 số không âm)
Đẳng thức xảy ra khi \(x=y=z=\frac{1}{2}\)

Ta có : \(\frac{x}{x^2-yz+2010}+\frac{y}{y^2-xz+2010}+\frac{z}{z^2-xy+2010}\)
\(=\frac{x^2}{x^3-xyz+2010x}+\frac{y^2}{y^3-xyz+2010y}+\frac{z^2}{z^3-xyz+2010z}\)
\(\ge\frac{\left(x+y+z\right)^2}{x^3+y^3+z^3-3xyz+2010\left(x+y+z\right)}=\frac{\left(x+y+z\right)^2}{x^3+y^3+z^3-3xyz+3\left(xy+yz+xz\right)\left(x+y+z\right)}\)
\(=\frac{\left(x+y+z\right)^2}{x^3+y^3+z^3+3xy^2+3x^2y+3x^2z+3xz^2+3y^2z+3yz^2}=\frac{\left(x+y+z\right)^2}{\left(x+y+z\right)^3}=\frac{1}{x+y+z}\)
\(C=\frac{4ab}{a+2b}+\frac{9ac}{4c+a}+\frac{4bc}{b+c}=\frac{4abc}{ac+2bc}+\frac{9abc}{4bc+ab}+\frac{4abc}{ab+ac}\)
\(\ge\frac{\left(2\sqrt{abc}+3\sqrt{abc}+2\sqrt{abc}\right)^2}{ac+2bc+4bc+ab+ab+ac}=\frac{49abc}{2ac+6bc+2ab}=7\)
Xin bổ sung cách sau, bn có thể tham khảo thêm
:\(GT\Leftrightarrow\frac{2}{c}+\frac{6}{a}+\frac{2}{b}=7\)
Đặt \(\hept{\begin{cases}\frac{1}{c}=x\\\frac{1}{b}=y\\\frac{3}{a}=z\end{cases}}\) Ta có: \(2\left(x+y+z\right)=7\)
Suy ra \(C=\frac{4}{4y+\frac{2z}{3}}+\frac{9}{x+\frac{4z}{3}}+\frac{4}{x+y}\ge\frac{\left(2+3+2\right)^2}{2\left(x+y+z\right)}=7\) (Bdt Cauchy-Schwarz)
Dấu = khi \(\hept{\begin{cases}a=2\\b=c=1\end{cases}}\)