Cô Thương Hoài thân ái chào toàn thể các thành viên của Olm. Vừa mới khai giảng chưa kịp vui niềm vui tựu trường miền bắc đã buồn nỗi buồn bão táp. Nhiều học sinh phải nghỉ học để tránh bão, Hà Nội, cây đổ, có người thương vong thật đau lòng. Các bạn thì sao, nơi các em sống có bão không, như thế nào rồi. Hãy cùng nhau chia sẻ tình hình tại đây nhé. Mong các em bình an.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


năm học mới đã đến rồi, vào năm học mới em chúc:
- trường: em chúc tất cả thầy cô và các bạn học sinh một năm học mới tràn đầy tích cực, vui vẻ. Em mong rằng thầy cô sẽ luôn dìu dắt chúng em đến tương lai ước mơ, chúc cho các bạn học sinh luôn phấn đấu học tập thật giỏi để xứng đáng với danh hiệu con ngoan trò giỏi nhé.
- OLM: Em mong rằng OLM sẽ ngày càng phát triển thật rực rỡ hơn nữa, và các bạn học sinh hãy tham gia học cùng OLM nhé, thú vị lắm. Chúc thầy cô OLM thật nhiều niềm vui và sức khỏe ạ!
Trong năm học mới, em chúc:
\(+\) Trường học: Các bạn cũng như cô có sức khỏe tốt để tiếp tục quá trình giảng dạy cũng như học tập tốt, để có nền tri thức tốt nhất cho đất nước.
\(+\) Olm: Phát triển rực rỡ đặc biệt sau năm nay hơn nhiều ạ.

em tên là Lê Phương Thảo.Điều e thấy thú vị nhất trong olm là ;
olm rất hay vì có thể hỏi bài, chat, nhắn tin với bạn bè,và có thể tham gia nhiều hoạt động như: văn hay mỗi tuần,toán vui mỗi tuần,fun english đều có rất nhiều giải thưởng
diều thứ 2 là giúp em học hỏi tìm kiếm đc rất nhiều điều hay lẽ phải và nhiều cuộc thi mang tầm pháp luật :)

em mới năm nay lên lớp 6 thôi nhưng vì em học tiếng anh sớm nên em có làm được một đoạn văn tiếng anh giống với đề bài,một số từ ngữ em không biết nên dùng sách tham khảo ạ:School days in the past for fifth graders were a mix of routine and fun. Classes started early, around 8 a.m., with subjects like math, reading, and science. Students used chalk and blackboards, and textbooks were often well-worn. During breaks, kids played outside, enjoying games like tag or jump rope. Summer holidays were a highlight, offering endless days for playing with friends, exploring nature, or visiting family. Getting to school might mean walking, biking, or taking a horse-drawn carriage. These simpler times were filled with laughter, learning, and the excitement of childhood adventures.

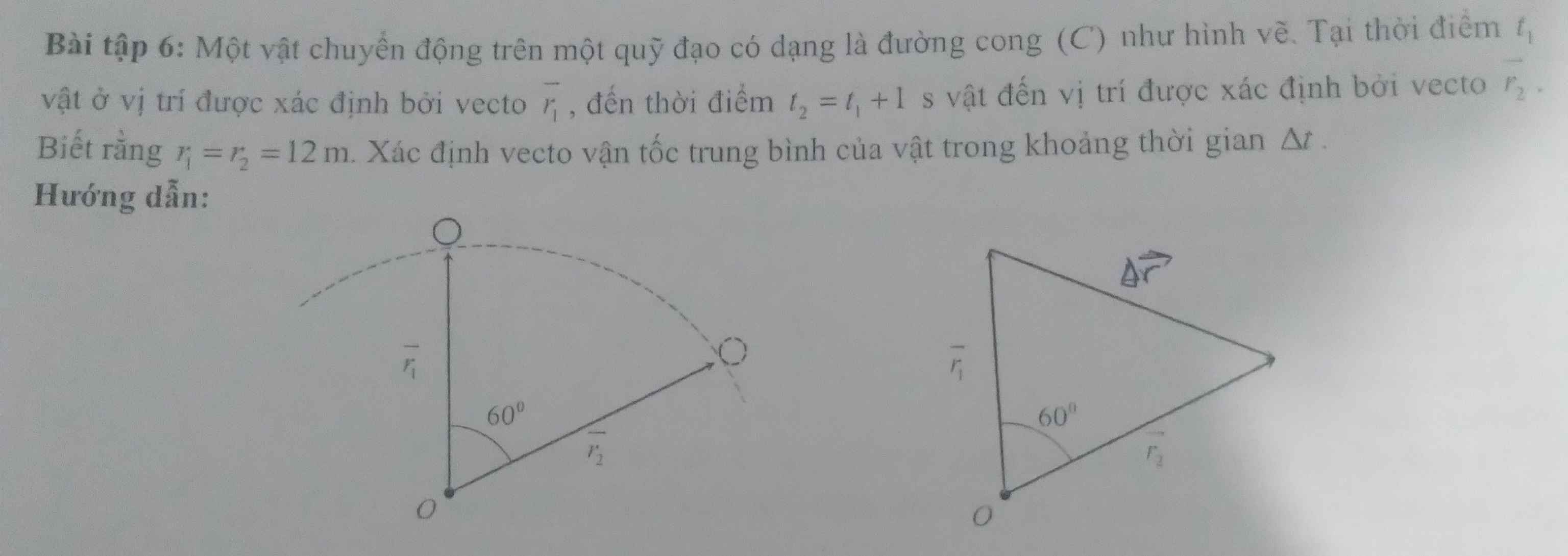
Vectơ vận tốc trung bình có phương và chiều trùng với vectơ độ dời

Độ lớn của vận tốc trung bình được tính như sau:
$|\overrightarrow{v_{tb}}|=\dfrac{|\overrightarrow{\Delta r}|}{\Delta t}=\dfrac{12}{1}=12$ (m/s)
(Do tam giác tạo bởi các vectơ $\overrightarrow{r_1},\,\overrightarrow{r_2},\,\overrightarrow{\Delta r}$ đều)

Dao động điều hòa có mặt khắp nơi trong cuộc sống hàng ngày và trong nhiều lĩnh vực kỹ thuật, từ những ứng dụng đơn giản đến những hệ thống phức tạp. Dưới đây là một số ứng dụng nổi bật:
- Đồng hồ quả lắc: Đồng hồ quả lắc sử dụng dao động điều hòa của quả lắc để giữ thời gian. Sự chính xác của nó dựa trên chu kỳ dao động không đổi của quả lắc. Dùng trong đồng hồ treo tường, đồng hồ đứng cổ điển.
- Các hệ thống treo xe: Hệ thống treo của xe sử dụng lò xo và giảm xóc để hấp thụ xung lực từ mặt đường, tạo ra dao động điều hòa giúp cải thiện độ êm ái và ổn định cho xe. Dùng trong hầu hết các loại xe từ ô tô, xe máy đến xe đạp.
- Âm nhạc và âm thanh: Các nhạc cụ như đàn guitar, đàn piano, và kèn sử dụng dao động điều hòa của dây đàn hoặc cột không khí bên trong để tạo ra âm thanh. Dùng trong sản xuất âm nhạc, thiết kế âm thanh trong rạp hát và phòng thu.
- Kỹ thuật điện và điện tử: Các mạch dao động, bao gồm lò xo điện từ (cuộn cảm) và tụ điện, tạo ra dao động điều hòa dùng trong việc truyền và nhận tín hiệu. Ứng dụng trong điện thoại di động, radio, truyền hình, và các thiết bị viễn thông khác.
- Y học: Máy đo rung tim sử dụng dao động điều hòa để ghi lại hoạt động của tim, giúp phát hiện các bất thường. Nó có tác dụng chẩn đoán và theo dõi sức khỏe tim mạch.
- Kỹ thuật xây dựng: Tính toán dao động điều hòa giúp thiết kế các công trình có khả năng chịu đựng các rung động do gió, động đất, hoặc giao thông. Nó được ứng dụng trong việc làm cầu treo, tòa nhà chọc trời, đập nước.
Tóm lại, dao động điều hoà không chỉ là một chủ đề lý thú trong lĩnh vực vật lý mà còn có ảnh hưởng sâu rộng đến thế giới xung quanh chúng ta, từ cấu trúc của các công trình kiến trúc đến thiết kế của các thiết bị điện tử.
Việc hiểu biết sâu sắc về dao động điều hoà mở ra cánh cửa cho những tiến bộ kỹ thuật và công nghệ, nhấn mạnh tầm quan trọng của nó trong nghiên cứu và ứng dụng khoa học ngày nay.
Dao động điều hòa có mặt khắp nơi trong cuộc sống hàng ngày và trong nhiều lĩnh vực kỹ thuật, từ những ứng dụng đơn giản đến những hệ thống phức tạp. Dưới đây là một số ứng dụng nổi bật:
· Đồng hồ quả lắc: Đồng hồ quả lắc sử dụng dao động điều hòa của quả lắc để giữ thời gian. Sự chính xác của nó dựa trên chu kỳ dao động không đổi của quả lắc. Dùng trong đồng hồ treo tường, đồng hồ đứng cổ điển.
· Các hệ thống treo xe: Hệ thống treo của xe sử dụng lò xo và giảm xóc để hấp thụ xung lực từ mặt đường, tạo ra dao động điều hòa giúp cải thiện độ êm ái và ổn định cho xe. Dùng trong hầu hết các loại xe từ ô tô, xe máy đến xe đạp.
· Âm nhạc và âm thanh: Các nhạc cụ như đàn guitar, đàn piano, và kèn sử dụng dao động điều hòa của dây đàn hoặc cột không khí bên trong để tạo ra âm thanh. Dùng trong sản xuất âm nhạc, thiết kế âm thanh trong rạp hát và phòng thu.
· Kỹ thuật điện và điện tử: Các mạch dao động, bao gồm lò xo điện từ (cuộn cảm) và tụ điện, tạo ra dao động điều hòa dùng trong việc truyền và nhận tín hiệu. Ứng dụng trong điện thoại di động, radio, truyền hình, và các thiết bị viễn thông khác.
· Y học: Máy đo rung tim sử dụng dao động điều hòa để ghi lại hoạt động của tim, giúp phát hiện các bất thường. Nó có tác dụng chẩn đoán và theo dõi sức khỏe tim mạch.
· Kỹ thuật xây dựng: Tính toán dao động điều hòa giúp thiết kế các công trình có khả năng chịu đựng các rung động do gió, động đất, hoặc giao thông. Nó được ứng dụng trong việc làm cầu treo, tòa nhà chọc trời, đập nước.
Tóm lại, dao động điều hoà không chỉ là một chủ đề lý thú trong lĩnh vực vật lý mà còn có ảnh hưởng sâu rộng đến thế giới xung quanh chúng ta, từ cấu trúc của các công trình kiến trúc đến thiết kế của các thiết bị điện tử.
Việc hiểu biết sâu sắc về dao động điều hoà mở ra cánh cửa cho những tiến bộ kỹ thuật và công nghệ, nhấn mạnh tầm quan trọng của nó trong nghiên cứu và ứng dụng khoa học ngày nay.

Em đăng kí nhận thưởng của câu lạc bộ chiến binh olm tháng 6 năm 2024

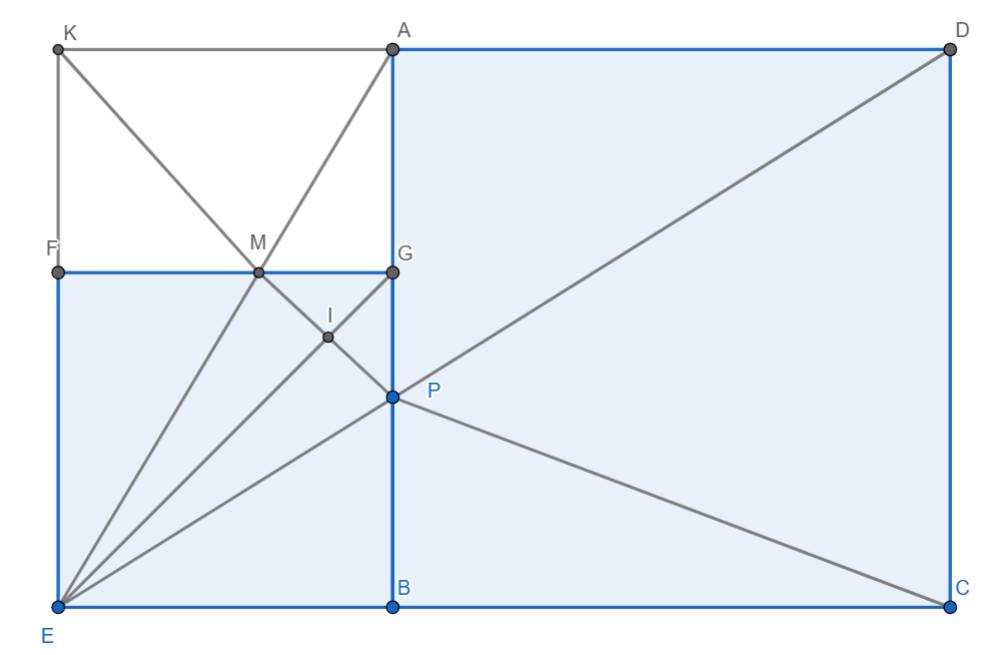
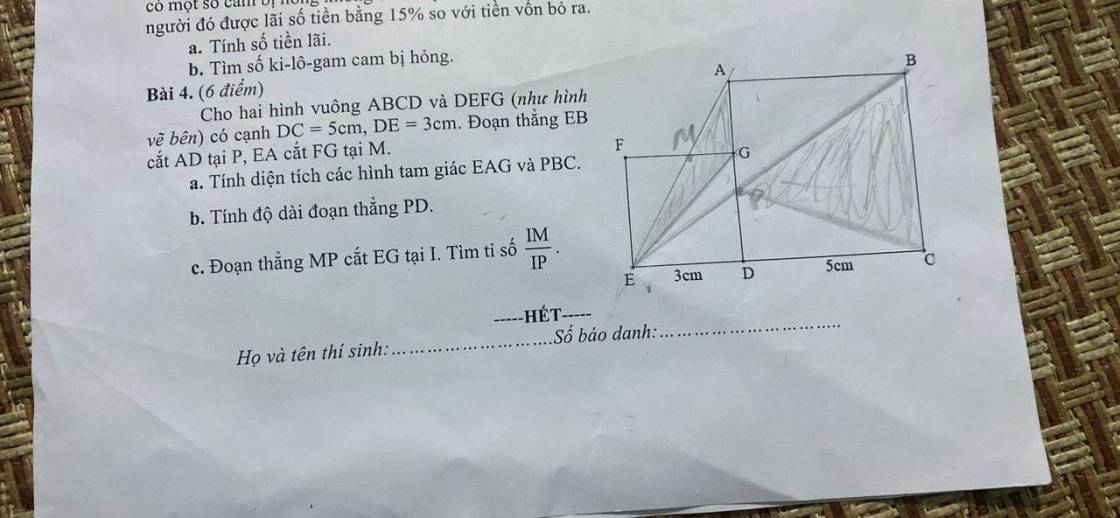
a) \(S_{EAG}=\dfrac{1}{2}\times AG\times ED=\dfrac{1}{2}\times2\times3=3\left(cm^2\right)\)
\(S_{PBC}=\dfrac{1}{2}\times BC\times DC=\dfrac{1}{2}\times5\times5=12,5\left(cm^2\right)\)
b) Ta có:
\(S_{EBC}=\dfrac{1}{2}\times BC\times EC=\dfrac{1}{2}\times5\times8=20\left(cm^2\right)\)
\(S_{PEC}=S_{ECB}-S_{PBC}=20-12,5=7,5\left(cm^2\right)\)
Vậy nên:
\(PD=\dfrac{2\times S_{PEC}}{EC}=\dfrac{2\times7,5}{8}=1,875\left(cm\right)\)
c) Ta thấy:
\(\dfrac{IM}{IP}=\dfrac{S_{MIG}}{S_{IPG}}=\dfrac{S_{MIE}}{S_{IPE}}\) nên \(\dfrac{IM}{IP}=\dfrac{S_{MGE}}{S_{GPE}}=\dfrac{\dfrac{1}{2}\times MG\times3}{\dfrac{1}{2}\times GP\times3}=\dfrac{MG}{GP}\)
Kéo dài AD cắt EF tại K.
Ta có \(S_{AKM}=\dfrac{1}{2}\times3\times2=3\left(cm^2\right)\)
nên \(S_{EKM}=S_{AKE}-S_{AKM}=\dfrac{1}{2}\times3\times5-3=4,5\left(cm^2\right)\)
Vậy \(FM=\dfrac{2\times S_{EKM}}{KE}=1,8\left(cm\right)\)
Thế thì \(MG=3-1,8=1,2\left(cm\right)\)
Lại có \(GP=3-1,875=1,125\left(cm\right)\)
Vậy nên:
\(\dfrac{IM}{IP}=\dfrac{MG}{GP}=\dfrac{1,2}{1,125}=\dfrac{16}{15}\).


mưa chưa to nhưng gió thì nguy hiểm kha khá rồi cô ạ
Bão sắp đến tỉnh em rồi cô ạ!