Tổng quãng đường đi được thì có lẽ là : 8 + 3 + 4 = 15km

Nhưng độ lớn dịch chuyển thì đơn giản chỉ là 4 km. Để làm được chúng ta cần vẽ ra giấy hoặc có thể tưởng tượng nhưng mà phải biết các hướng đông tây nam bắc. Khi biết rồi thì rất dễ. Chúc học tốt !!

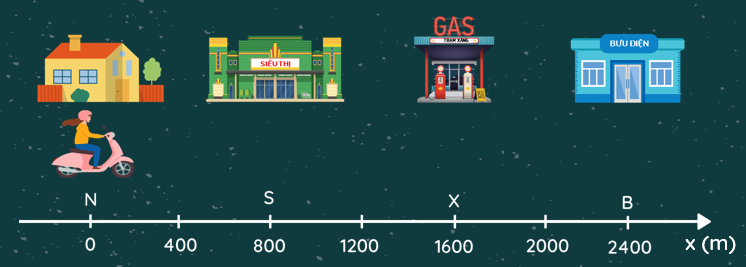
quãng đường người đó đã đi:

S = NS+NB = 800+2400 =3200m=3.2km

độ dời của người đó bằng khoảng cách từ vị trí ban đầu đến bưu điện bằng NB = 2400m = 2.4km

Quãng đường người đó đã đi được là: \(NS+SX+XN+NB=800+\left(1600-800\right)+1600+2400=5600\left(km\right)\)

Độ dời của người đó là: \(NS+SX-XN+NB=800+\left(1600-800\right)-1600+2400=2400\left(km\right)\)

Đề bài khó quá không biết là sau khi bán 3 cửa hàng có số qye test bằng nhau là:

1/ Số que bán của 3 cửa hàng bằng nhau 

2/ Số que còn lại bằng nhau

Nếu số que còn lại bằng nhau thì:

Phân số chỉ số que còn lại của cửa hàng thứ nhất là

\(1-\dfrac{5}{8}=\dfrac{3}{8}\) số que cửa hàng 1

Phân số chỉ số que còn lại của cửa hàng thứ hai là

\(1-\dfrac{2}{3}=\dfrac{1}{3}\) số que cửa hàng 2

Phân số chỉ số que còn lại của cửa hàng thứ ba là

\(1-\dfrac{1}{4}=\dfrac{3}{4}\) số que cửa hàng 3

Theo đề bài

3/8 sô que CH1 = 1/3 số que CH2 = 3/4 số que CH3

=> 3/8 sô que CH1 = 3/9 số que CH2 = 3/4 số que CH3

=> 1/8 sô que CH1 = 1/9 số que CH2 = 1/4 số que CH3

Chia số que CH1 thành 8 phần thì số que CH2 là 9 phần số que CH3 là 4 phần

Tổng số phần bằng nhau là

8+9+4=21 phần

Giá trị 1 phần là

630:21=30 que

Số que CH1 là

30x8=240 que

Số que CH2 Là

30x9=270 que

Số que CH3 là

30x4=120 que

Áp dụng BĐT Cosi cho 2 số dương:

\(x^4+yz\ge2\sqrt{x^4yz}=2x^2\sqrt{yz}\)

\(\Rightarrow\dfrac{x^2}{x^4+yz}\le\dfrac{x^2}{2x^2\sqrt{yz}}=\dfrac{1}{2\sqrt{yz}}\le\dfrac{1}{4}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)\)

Tương tự => \(\left\{{}\begin{matrix}\dfrac{y^2}{y^4+xz}\le\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{z}\right)\\\dfrac{z^2}{z^4+xy}\le\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\end{matrix}\right.\)

=> \(P\le\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)

Có \(x^2+y^2+z^2=3xyz\Leftrightarrow\dfrac{x}{yz}+\dfrac{y}{xz}+\dfrac{z}{xy}=3\left(1\right)\)

Áp dụng BĐT Cosi cho 2 số dương:

\(\dfrac{x}{yz}+\dfrac{y}{xz}\ge2\sqrt{\dfrac{x}{yz}.\dfrac{y}{xz}}=\dfrac{2}{z}\)

Tương tự => \(\left\{{}\begin{matrix}\dfrac{y}{xz}+\dfrac{z}{xy}\ge\dfrac{2}{x}\\\dfrac{z}{xy}+\dfrac{x}{yz}\ge\dfrac{2}{y}\end{matrix}\right.\)

Có: \(6=2\left(\dfrac{x}{yz}+\dfrac{y}{xz}+\dfrac{z}{xy}\right)\ge2\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)

\(\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\le3\)

\(\Leftrightarrow P\le\dfrac{3}{2}\)

Dấu "=" xảy ra <=> x = y = z = 1

A B C E D P Q O H K I

1/ E và D cùng nhìn BC dưới 2 góc bằng nhau và bằng 90 độ nên E và D cùng nằm trên đường tròn đường kính BD

=> BCDE là tứ giác nội tiếp

Xét tg vuông ABD và tg vuông ACE có

\(\widehat{ABP}=\widehat{ACQ}\) (cùng phụ với \(\widehat{BAC}\) ) (1)

\(sđ\widehat{ABP}=\dfrac{1}{2}sđ\) cung AP (góc nội tiếp) (2)

\(sđ\widehat{ACQ}=\dfrac{1}{2}sđ\) cung AQ (góc nội tiếp) (3)

Từ (1) (2) (3) => sđ cung AP = sđ cung AQ

2/ 

Ta có 

\(sđ\widehat{ABP}=\dfrac{1}{2}sđ\) cung AP (góc nt) (1)

\(sđ\widehat{ABQ}=\dfrac{1}{2}sđ\) cung AQ (góc nt) (2)

Mà sđ cung AP = sđ cung AQ (cmt) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{ABP}=\widehat{ABQ}\) => BA là phân giác của \(\widehat{PBQ}\)

Mà \(AB\perp CQ\) => BA là đường cao của tg HBQ

=> tg HBQ cân tại B (trong tg đường phân giác đồng thời là đường cao thì tg đó là tg cân)

=> EQ=EH (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến) => E là trung điểm của HQ (đpcm)

Chứng minh tương tự ta cũng có D là trung điểm của HP

=> ED là đường trung bình của tg HPQ => ED//PQ

Nối AO cắt (O) tại K ta có

sđ cung AQK = sđ cung APK (nửa đường tròn)

sđ cung AQ = sđ cung AP (cmt)

=> sđ cung QBK = sđ cung PCK => KQ=KP (hai cung có số đo bằng nhau thì hai dây trương cung tương ứng có độ dài bằng nhau) => tg KPQ cân tại K

Ta có

\(sđ\widehat{AKQ}=\dfrac{1}{2}sđ\) cung AQ (góc nt)

\(sđ\widehat{AKP}=\dfrac{1}{2}sđ\) cung AP (góc nt)

Mà sđ cung AQ = sđ cung AP (cmt)

=> \(\widehat{AKQ}=\widehat{AKP}\) => AK là phân giác  \(\widehat{PKQ}\) của tg cân KPQ 

=> AK là đường cao của tg KPQ (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)

\(\Rightarrow AK\perp PQ\Rightarrow OA\perp PQ\) mà DE//PQ (cmt) \(\Rightarrow OA\perp DE\) (đpcm)

3/ Ta có

Xét tg vuông ABD có

\(\widehat{ABD}=90^o-\widehat{CAB}=90^o-60^o=30^o\)

\(\Rightarrow AD=\dfrac{AB}{2}\) (trong tg vuông cạnh đối diện với góc \(30^o\) bằng nửa cạnh huyền)

C/m tương tự khi xét tg vuông ACE ta cũng có \(AE=\dfrac{AC}{2}\)

Ta có

\(sđ\widehat{ADB}=30^o=\dfrac{1}{2}sđ\) cung AP => sđ cung AP\(=60^o\) = sđ cung AQ

Gọi I là giao của AK với PQ ta có

tg KPQ cân tại K (cmt)

\(AK\perp PQ\) (cmt)

=> IQ=IP (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)

Xét tg vuông AQI có

\(sđ\widehat{AQI}=\dfrac{1}{2}sđ\) cung AP = \(30^o\Rightarrow AI=\dfrac{AQ}{2}\)  (trong tg vuông cạnh đối diện với góc 30 độ bằng nửa cạnh huyền)

Ta có \(\widehat{AQK}=90^o\) (góc nt chắn nửa đường tròn)

Xét tg vuông AQK có

\(AQ^2=AI.AK=\dfrac{AQ}{2}.2R\Rightarrow AQ=R\Rightarrow AI=\dfrac{AQ}{2}=\dfrac{R}{2}\) 

\(\Rightarrow IK=AK-AI=2R-\dfrac{R}{2}=\dfrac{3R}{2}\)

Ta có

\(IQ^2=IA.IK\) (trong tg vuông bình phươn đường cạo hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa hình chiếu của 2 cạnh góc vuông trên cạnh huyền)

\(\Rightarrow IQ^2=\dfrac{R}{2}.\dfrac{3R}{2}\Rightarrow IQ=\dfrac{R\sqrt{3}}{2}\)

Ta có 

IQ=IP (cmt) => PQ=2.IQ=\(R\sqrt{3}\)

Ta có ED là đường trung bình của tg HPQ (cmt)

\(\Rightarrow DE=\dfrac{PQ}{2}=\dfrac{R\sqrt{3}}{2}\)

Ta có

\(S_{ABC}=\dfrac{1}{2}.AB.AC.\sin\widehat{CAB}=\dfrac{1}{2}.AB.AC.\dfrac{\sqrt{3}}{2}=\dfrac{AB.AC.\sqrt{3}}{4}\)

\(S_{AED}=\dfrac{1}{2}.AD.AE.\sin\widehat{CAB}=\dfrac{1}{2}.\dfrac{AB}{2}.\dfrac{AC}{2}.\dfrac{\sqrt{3}}{2}=\dfrac{AB.AC.\sqrt{3}}{16}\)

\(\Rightarrow\dfrac{S_{AED}}{S_{ABC}}=\dfrac{1}{4}\)

Gọi R' là bán kính đường tròn ngoại tiếp tg AED

\(S_{AED}=\dfrac{AE.AD.DE}{4R'}=\dfrac{AC}{2}.\dfrac{AB}{2}.\dfrac{6\sqrt{3}}{2}.\dfrac{1}{4R'}=\dfrac{AB.AC.\sqrt{3}}{4}.\dfrac{3\sqrt{3}}{4R'}=\dfrac{S_{ABC}.3\sqrt{3}}{4R'}\)

\(\Rightarrow\dfrac{S_{AED}}{S_{ABC}}=\dfrac{3\sqrt{3}}{4R'}=\dfrac{1}{4}\Rightarrow R'=3\sqrt{3}\)

1)

ĐKXĐ: \(x\ge\dfrac{1}{4}\)

PT \(\Leftrightarrow\sqrt{4x^2+2x+2}-\sqrt{4x-1}+2x^2+3x-3=0\)

\(\Leftrightarrow\left(\sqrt{4x^2+2x+2}-2\right)-\left(\sqrt{4x-1}-1\right)+2x^2+3x-2=0\)

\(\Leftrightarrow\dfrac{4x^2+2x+2-4}{\sqrt{4x^2+2x+2}+2}-\dfrac{4x-1-1}{\sqrt{4x-1}+1}+\left(2x-1\right)\left(x+2\right)=0\)

\(\Leftrightarrow\dfrac{4x^2+2x-2}{\sqrt{4x^2+2x+2}+2}-\dfrac{4x-2}{\sqrt{4x-1}+1}+\left(2x-1\right)\left(x+2\right)=0\)

\(\Leftrightarrow\dfrac{2\left(2x-1\right)\left(x+1\right)}{\sqrt{4x^2+2x+2}+2}-\dfrac{2\left(2x-1\right)}{\sqrt{4x-1}+1}+\left(2x-1\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left(2x-1\right)\left(\dfrac{2x+2}{\sqrt{4x^2+2x+2}+2}-\dfrac{2}{\sqrt{4x-1}+1}+x+2\right)=0\)

Mà \(\dfrac{2x+2}{\sqrt{4x^2+2x+2}+2}>0\)

       \(\dfrac{2}{\sqrt{4x-1}+1}< 2\Leftrightarrow-\dfrac{2}{\sqrt{4x-1}+1}>-2\)

        \(x+2>2\)

=> \(\dfrac{2x+2}{\sqrt{4x^2+2x+2}+2}-\dfrac{2}{\sqrt{4x-1}+1}+x+2>0\)

\(\Leftrightarrow2x-1=0\Leftrightarrow x=\dfrac{1}{2}\left(TM\right)\)

KL: Vậy PT có nghiệm \(S=\left\{\dfrac{1}{2}\right\}\)

2)

BĐT \(\Leftrightarrow\left[\dfrac{a^3}{b+2c}+\dfrac{b+2c}{9}.a\right]+\left[\dfrac{b^3}{c+2a}+\dfrac{c+2a}{9}.b\right]+\left[\dfrac{c^3}{a+2b}+\dfrac{a+2b}{9}.c\right]-\dfrac{1}{3}.\left(ab+bc+ca\right)\ge1\)

Áp dụng BĐT Cosi cho 2 số không âm:

\(\dfrac{a^3}{b+2c}+\dfrac{b+2c}{9}.a\ge2.\sqrt{\dfrac{a^3}{b+2c}.\dfrac{b+2c}{9}.a}=\dfrac{2a^2}{3}\)

Tương tự \(\Rightarrow\left\{{}\begin{matrix}\dfrac{b^3}{c+2a}+\dfrac{c+2a}{9}.b\ge\dfrac{2b^2}{3}\\\dfrac{c^3}{a+2b}+\dfrac{a+2b}{9}.c\ge\dfrac{2c^2}{3}\end{matrix}\right.\)

\(VT\ge\dfrac{2}{3}\left(a^2+b^2+c^2\right)-1\)

Mà \(a^2+b^2+c^2\ge ab+bc+ca=3\)

\(\Rightarrow VT\ge1\left(đpcm\right)\)

Dấu "=" xảy ra \(\Leftrightarrow a=b=c=1\)

2. Sử dụng bất đẳng thức Cauchy-Schwarz:
\(LHS\ge\sum_{cyc}\dfrac{a^4}{ab+2ca}\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{3\left(ab+bc+ca\right)}\ge\dfrac{\left(ab+bc+ca\right)^2}{3\left(ab+bc+ca\right)}=\dfrac{ab+bc+ca}{3}=\dfrac{3}{3}=1\)Vậy ta có điều phải chứng minh

1. Khi $m=4$ thì phương trình trở thành $x^2-9x+20=0\Leftrightarrow (x-4)(x-5)=0$ hay $x=4$ hoặc $x=5$ là các nghiệm của phương trình.

2. Ta có \(\Delta=\left(2m+1\right)^2-4\left(m^2+m\right)=1>0\) nên phương trình luôn có 2 nghiệm phân biệt, hơn thế nữa ta có $x^2-(2m+1)x+m^2+m=0$ có 2 nghiệm là $x_1,x_2$ thì theo định lý Viete ta có $x_1+x_2=2m+1,x_1.x_2=m^2+m$, ta có $-17=(x_1+x_2)^2-7x_1.x_2=(2m+1)^2-7(m^2+m)$ hay $-3m^2-3m+18=0\Leftrightarrow 3(m+3)(m-2)=0$, vậy $m=2,m=-3$ là các giá trị cần tìm 

\(\left\{{}\begin{matrix}\left(x^2-2x-9\right)\sqrt{x^2-x-6}=0\left(1\right)\\x+y=0\left(2\right)\end{matrix}\right.\)

ĐK: \(\left[{}\begin{matrix}x\ge3\\x\le-2\end{matrix}\right.\)

Từ (1) <=> \(\left[{}\begin{matrix}x^2-2x-9=0\left(\cdot\right)\\x^2-x-6=0\end{matrix}\right.\) (*) nghiệm không tm đk

<=> \(\left[{}\begin{matrix}x=3\left(I\right)\\x=-2\left(II\right)\end{matrix}\right.\) -> 

Từ (2) => y = -x 

(I) y = -3

(II) y = 2

Với x = 3 và y = -3 => P = 3² + (-3)² + 2020 = 2038

với x = -2 và y = 2 => P = (-2)² + 2² + 2020 = 2028

cho mn hỏi là (*) tìm ra nghiệm là \(x=1-\sqrt{10}=-2,1622....\) và \(x=1+\sqrt{10}=4,1622.....\)

tại sao lại bị loại vậy (dựa vào ĐKXĐ kiểu j mà bị loại), mn ko rõ lắm