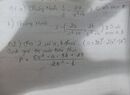trên bảng ô vuông kích thước 8x8, ta viết các số tự nhiên từ 1-> 64 mỗi số viết vào một ô một cách tùy ý. Chứng minh rằng luôn tồn tại 2 ô vuông chung cạnh mà hiệu các số ghi trong chúng không nhỏ hơn 5 (chứng minh theo nguyên lý Dirichlet)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
4 tháng 12 2020
c) ( x2 + x + 1 )( x2 + x + 2 ) - 12
Đặt t = x2 + x + 1
<=> t( t + 1 ) - 12
= t2 + t - 12
= t2 - 3t + 4t - 12
= t( t - 3 ) + 4( t - 3 )
= ( t - 3 )( t + 4 )
= ( x2 + x + 1 - 3 )( x2 + x + 1 + 4 )
= ( x2 + x - 2 )( x2 + x + 5 )
= ( x2 - x + 2x - 2 )( x2 + x + 5 )
= [ x( x - 1 ) + 2( x - 1 ) ]( x2 + x + 5 )
= ( x - 1 )( x + 2 )( x2 + x + 5 )
d) ( x + 2 )( x + 3 )( x + 4 )( x + 5 ) - 24
= [ ( x + 2 )( x + 5 ) ][ ( x + 3 )( x + 4 ) ] - 24
= ( x2 + 7x + 10 )( x2 + 7x + 12 ) - 24
Đặt t = x2 + 7x + 10
<=> t( t + 2 ) - 24
= t2 + 2t - 24
= t2 - 4t + 6t - 24
= t( t - 4 ) + 6( t - 4 )
= ( t - 4 )( t + 6 )
= ( x2 + 7x + 10 - 4 )( x2 + 7x + 10 + 6 )
= ( x2 + 7x + 6 )( x2 + 7x + 16 )
= ( x2 + 6x + x + 6 )( x2 + 7x + 16 )
= [ x( x + 6 ) + ( x + 6 ) ]( x2 + 7x + 16 )
= ( x + 6 )( x + 1 )( x2 + 7x + 16 )
NC
4 tháng 12 2020
a, Sửa đề:\(\left(x^2+x\right)^2-2\left(x^2+x\right)-15\)
Đặt \(t=x^2+x\)
\(\Rightarrow t^2-2t-15\)
\(=t^2-5t+3t-15\)
\(=t\left(t-5\right)+3\left(t-5\right)\)
\(=\left(t+3\right)\left(t-5\right)\)
\(=\left(x^2+x+3\right)\left(x^2+x-5\right)\)
b,\(x^2+2xy+y^2-x-y-12\)
\(=\left(x+y\right)^2-\left(x+y\right)-12\)
Đặt \(t=x+y\)
\(\Rightarrow t^2-t-12\)
\(=t^2-4t+3t-12\)
\(=t\left(t-4\right)+3\left(t-4\right)\)
\(=\left(t+3\right)\left(t-4\right)\)
\(=\left(x+y+3\right)\left(x+y-4\right)\)
c,\(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt \(t=x^2+x+1\)
\(\Rightarrow t\left(t+1\right)-12\)
\(=t^2+t-12\)
\(=t^2-3t+4t-12\)
\(=t\left(t-3\right)+4\left(t-3\right)\)
\(=\left(t+4\right)\left(t-3\right)\)
\(=\left(x^2+x+5\right)\left(x^2+x-2\right)\)
\(=\left(x^2+x+5\right)\left(x^2-x+2x-2\right)\)
\(=\left(x^2+x+5\right)\left[x\left(x-1\right)+2\left(x-1\right)\right]\)
\(=\left(x^2+x+5\right)\left(x+2\right)\left(x-1\right)\)
d,\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x+2\right)\left(x+5\right)\left(x+3\right)\left(x+4\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
Đặt \(t=x^2+7x+10\)
\(\Rightarrow t\left(t+2\right)-24\)
\(=t^2+2t-24\)
\(=t^2-4t+6t-24\)
\(=t\left(t-4\right)+6\left(t-4\right)\)
\(=\left(t+6\right)\left(t-4\right)\)
\(=\left(x^2+7x+16\right)\left(x^2+7x+6\right)\)
\(=\left(x^2+7x+16\right)\left(x^2+x+6x+6\right)\)
\(=\left(x^2+7x+16\right)\left[x\left(x+1\right)+6\left(x+1\right)\right]\)
\(=\left(x^2+7x+16\right)\left(x+6\right)\left(x+1\right)\)
I
1 tháng 12 2020
a) ABCD là hcn => AB//CD; AB=CD ; AD=BC
mà AF//CK
=> AKCF là hbh
=> AF=CK
=. tam giác ADE= tam giác CBK ( ch-gcz)
b) M là trung điểm của AE ; MN//AD
=> MN là đường trung bình của tam giác ADE
=> MN=1/2AD
BC//AD , BC=AD; Q là trung điểm của BC nên BQ//AD; BQ=1/2AD
=> MN//BQ zà MN=BQ=> MNBQ là hbh
=> góc NMB = góc NQB
c) góc AQN = góc BQN - góc BQA=góc BMN -(90độ - góc QAB)
=góc QAB +góc BMN-90 độ
ta có góc BMN = góc BME +NME = góc MAB +MBA+ADE
=> BMN=MBA+ 90 đô
=> góc AQN=QAB+MBA+90 độ - 90độ=QAB+MBA(1)
tam giác AED ~ tam giác BEA (g-g)
=> AD/BA=DE/AE=2DN/2MA=DN/MA
=> tam giác AMB ~ tam giác DNA (c-g-c)
=> góc ABM = góc DAN (2)
từ 1 zà 2 => dpcm
X
0
2 tháng 12 2020
III. Combine each pair of sentences to make one sentence, using the words given in the box.
otherwise and so but
1. Maria didn’t do any revision. she didn’t pass the exam. …………………SO……………………………………………………………….
2. He’s overweight. He continues to eat lots of cakes and biscuits.…………………………BUT……………………………………………………….
3.You need to work harder. You won’t get a passing grade.…………………OTHERWISE
4. During Tet, Vietnamese people buy all kinds of sweets. They make Chung cakes as well.……………………AND……………………………………………………………………..….