ta có \(\sqrt{\left(a+c\right)\left(a+b\right)}\ge a+\sqrt{bc}\left(1\right)\)

thật vậy \(\left(1\right)\Leftrightarrow\left(a+c\right)\left(a+b\right)\ge a^2+2a\sqrt{bc}+bc\)

\(\Leftrightarrow ab+ac\ge2a\sqrt{bc}\Leftrightarrow b+c\ge2\sqrt{bc}\)(đúng theo BĐT cosi)

cminh tương tự \(\Rightarrow\sqrt{\left(b+c\right)\left(b+a\right)}\ge b+\sqrt{ac};\sqrt{\left(c+a\right)\left(c+b\right)}\ge c+\sqrt{ab}\)

\(\Rightarrow\dfrac{a}{\sqrt{\left(a+c\right)\left(a+b\right)}}\le\dfrac{a}{a+\sqrt{bc}}=\dfrac{1}{1+\dfrac{\sqrt{bc}}{a}}\)

\(tt\Rightarrow P\le\dfrac{1}{1+\dfrac{\sqrt{bc}}{a}}+\dfrac{1}{1+\dfrac{\sqrt{ac}}{b}}+\dfrac{1}{1+\dfrac{\sqrt{ab}}{c}}\)

\(đặt\left(\dfrac{\sqrt{bc}}{a};\dfrac{\sqrt{ac}}{b};\dfrac{\sqrt{ab}}{c}\right)=\left(x;y;z\right)\Rightarrow xyz=1\)

\(\Rightarrow P\le\dfrac{1}{x+1}+\dfrac{1}{y+1}+\dfrac{1}{z+1}\)

ta đi chứng minh \(\dfrac{1}{x+1}+\dfrac{1}{y+1}+\dfrac{1}{z+1}\le\dfrac{3}{2}\)

\(\Leftrightarrow2\left(y+1\right)\left(z+1\right)+2\left(x+1\right)\left(z+1\right)+2\left(x+1\right)\left(y+1\right)\le3\left(x+1\right)\left(y+1\right)\left(z+1\right)\)

\(\Leftrightarrow2xy+2xz+2yz+4x+4y+4z+6\le3xyz+3+3xy+3xz+3yz+3x+3y+3z\)

ủa đến đây theo cách làm bth đúng rồi mà sao không ra nhỉ bạn xem lại hộ mình giống bài  n ày mình từng làm r

https://hoc24.vn/vip/289470733648/page-12

Toán 9

em cảm ơn cô và olm chúc mừng tất cả các bạn có tên trong danh sách nhé

?

I'm don't know

14 balls are not blue.    => yellow + red + pink = 14
16 balls are not yellow. => blue + red + pink = 16
24 balls are not red.      => blue + yellow + pink = 24
12 balls are not pink.    => blue + yellow + red = 12

====> 3 yellow + 3 red + 3 blue + 3 pink = 14+16+24+12
    3(yellow + red + blue + pink) = 66
    yellow + red + blue + pink = 66:3 =22
 

Nếu là bạn anh ta,mik sẽ khuyên ko nên tham gia vì vòng 100 người có khả năng  người ra mặt 12 rất ,và cả 100 người đều sẽ C.H.Ế.T 😈😈😈

cái gì mà đe dọa đến tính mạng thì phương án tốt nhất là ko đi

\(\sqrt{5-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)

\(=\sqrt{5-\sqrt{3-\sqrt{\left(3-2\sqrt{5}\right)^2}}}\)

\(=\sqrt{5-\sqrt{6-2\sqrt{5}}}=\sqrt{5-\sqrt{\left(\sqrt{5}-1\right)^2}}\)

\(=\sqrt{1}=1\)

gọi C là điểm trùng với q1, \(H\in CH\cap AB\)

Xét tam giác CHA là tam giác vuông tại H

=> \(CA=\sqrt{AH^2+CH^2}=5\) cm ( AH=3cm; CH=4cm)

Ta có: \(F_{10}=K\dfrac{\left|q_1q_0\right|}{r^2}=9,10^9.\dfrac{\left|2.10^{-6}.2.10^{-6}\right|}{0,05^2}=14,4\) N

Áp dụng định lí cosin ta có:\(6^2=5^2+5^2-2.5.5.cos\alpha\)

                                            \(cos\widehat{C}=\dfrac{5^2+5^2-6^2}{2.5.5}=\dfrac{7}{25}\)

Dựa theo hình vẽ ta thấy: cos C= cos a

                     \(F_1=\sqrt{F_{10}^2+F^2_{10}+2F_{10}F_{10}cos\alpha}=23,04\)  N  

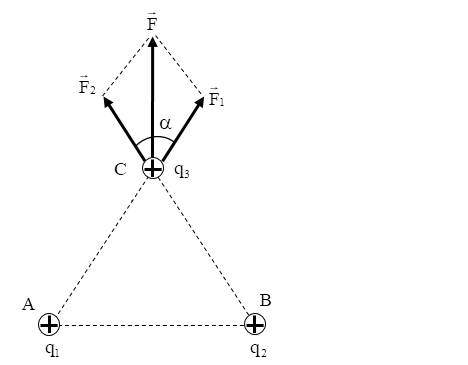                 (Hướng của lực sẽ như thế này, ảnh này chưa kẻ CH nha! )

Tổng số bạn đăng kí clb Tiếng Anh hoặc clb Nhạc hoặc cả `2` clb là:

              `16+19-9=26` (bạn)

Vậy còn lại số bạn không đăng kí câu lạc bộ nào là:

              `40-26=14` (bạn)

16

\(48=2^4.3\\ 36=2^2.3^2\\ \RightarrowƯCLN_{\left(48;36\right)}=2^2.3=12\\ \Rightarrow A\cap B=ƯC_{\left(48;36\right)}=Ư_{\left(12\right)}=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)

`A={1;2;3;4;6;8;12;16;24;48}`

`B={1;2;3;4;6;9;12;18;36}`

 `=>A nn B={1;2;3;4;6;12}`

Số h/s nam chiếm số phần h/s nữ là: `11/14`

Khối lớp `4` có số h/s nam là: `30:(14-11)xx11=110` (h/s)

Khối lớp `4` có số h/s nữ là: `110+30=140` (h/s)

Số hs nam chiếm số phần hs nữ là: $11/14$

Khối lớp 44 có số hs nam là: $30:(14-11)xx11=110$ (hs)

Khối lớp $4$ có số hs nữ là: $110+30=140$ (hs)