Cho hình vẽ sau:
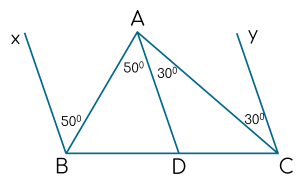
Chứng minh $Bx$ // $Cy$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


số tiền lãi mà mẹ minh được nhận sau 6 tháng là
2062400 - 2000000 = 62400 (đồng)
mỗi tháng số tiền lãi mà mẹ minh nhận được là
62400 : 6 = 10400 (đồng)
% lãi hàng tháng là
10400 : 2000000 x 100 = 0,52%
đs....
số tiền lãi mà mẹ minh được nhận sau 6 tháng là
2062400 - 2000000 = 62400 (đồng)
mỗi tháng số tiền lãi mà mẹ minh nhận được là
62400 : 6 = 10400 (đồng)
% lãi hàng tháng là
10400 : 2000000 x 100 = 0,52%

a)
\(\begin{matrix}N\left(x\right)=-4x^4+9x^3-x^2+5x+\dfrac{1}{3}\\^-M\left(x\right)=-x^4-9x^3+x^2+9x+\dfrac{4}{3}\\\overline{N\left(x\right)-M\left(x\right)=-3x^4+18x^3-2x^2-4x-1}\end{matrix}\)
b)
\(\begin{matrix}M\left(x\right)=-x^4-9x^3+x^2+9x+\dfrac{4}{3}\\^+N\left(x\right)=-4x^4+9x^3-x^2+5x+\dfrac{1}{3}\\\overline{M\left(x\right)+N\left(x\right)=-5x^4+14x+\dfrac{5}{3}}\end{matrix}\)

Rõ ràng các góc $\angle AOD,\angle BOC $ được đề cập là các góc không lớn hơn $180^o$.
Khi đó ta thấy rằng $\angle AOD,\angle BOC$ là hai góc đối đỉnh nên $\angle AOD=\angle BOC$, từ đó kết hợp giả thiết ta thu được $2\angle AOD=100^o$ hay $\angle AOD=\angle BOC=50^o$
Khi đó $\angle BOD=\angle AOC=180^o-\angle 50^o=130^o$

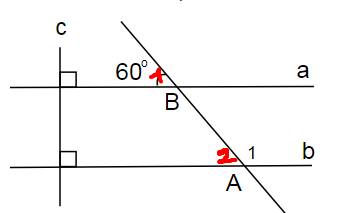
Vì a \(\perp\) c và b \(\perp\) c nên a//b
=>\(\hat{B_1}=\hat{A_2}\)=600 (hai góc đồng vị)
Mà \(\hat{A_2}\) và \(\hat{A_1}\)là hai góc kề bù
=> \(\hat{A_1}+\hat{A_2}=180^o\)
hay \(\hat{A_1}\) + 60o=180o
=> \(\hat{A_1}\) = 180o-60o=120o
Vậy \(\hat{A_1}\)=1200

Đổi: 0,9=9/10
Vì vận tốc và thời gian tỉ lệ nghịch với nhau
=>Thời gian mới bằng 10/9 lần thời gian cũ
Thời gian ô tô đó đi từ A đến B nếu nó đi với vận tốc mới bằng 0,9 lần vận tốc cũ là: 10,8x10/9=12 (giờ)
Đáp số: 12 giờ
Cho 2 đa thức f(x)=2x2+ax+4f(x)=2x2+ax+4 và g(x)=x2−5x−bg(x)=x2−5x−b (a,ba,b là hằng số)
Tìm các hệ số a,ba,b sao cho f(1)=g(2)f(1)=g(2) và

\(P=\dfrac{2x+3}{3x+1}\) là số nguyên suy ra \(3P=\dfrac{6x+9}{3x+1}=\dfrac{6x+2+7}{3x+1}=2+\dfrac{7}{3x+1}\inℤ\)
\(\Leftrightarrow\dfrac{7}{3x+1}\inℤ\Rightarrow3x+1\inƯ\left(7\right)=\left\{-7,-1,1,7\right\}\) (vì \(x\) nguyên)
\(\Leftrightarrow x\in\left\{0,2\right\}\) (vì \(x\) nguyên)
Thử lại đều thỏa mãn.

b.ta có M là trung điểm NC nên MC=MB
ta lại có N là trung điểm MB => MN=NB
vậy MC=2323MN
xét tgac ACD có NC là đường trung tuyến ứng với cạnh AD
mà M thuộc CN và MC=2323MN nên theo định nghĩa M là trọng tâm tgiac ACD
mặt khác E là trung điểm CD vậy AE là đường trung tuyến ứng với CD vậy A; M;E thẳng hàng
Tam giác ABC cân tại A do đó trung tuyến AM vuông góc với BC
Tam giác AMB vuông tại M theo định lý pi-ta-go ta có
AM.AM + MB.MB = AB.AB
=> AM.AM = 13x13 -5x5 =144
=> AM = 12cm
Vì \(\widehat{xBA}=\widehat{BAD}\left(=50^o\right)\) mà \(\widehat{xBA}\text{ và }\widehat{BAD}\) là 2 góc so le trong
=> Bx//AD (1)
Vì \(\widehat{DAC}=\widehat{ACy}\left(=30^o\right)\) mà \(\widehat{DAC}\text{ và }\widehat{ACy}\) là 2 góc so le trong
=> AD // Cy (2)
Từ (1) và (2) => Bx // Cy
Ta có:
`@` \(\widehat{ABx}=\widehat{DAB}=50^o\)
`=>Bx////AD` ( 2 góc so le trong bằng nhau ) (1)
`@`\(\widehat{ACy}=\widehat{DAC}=30^o\)
`=>Cy////AD` ( 2 góc so le trong bằng nhau ) (2)
\(\left(1\right);\left(2\right)\Rightarrow\)`Bx////Cy`