Một đa giác lồi \(n\) cạnh được chia thành các tam giác bằng cách vẽ \(n-3\) đường chéo đôi một không cắt nhau ở bên trong đa giác. Biết rằng ở mỗi đỉnh có một số lẻ các tam giác nhỏ. CMR \(n⋮3\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tranh do học sinh được đồ họa bằng máy tính thì có được tham gia không cô?
Khuyến khích các em sáng tạo không giới hạn, nên các em có thể vẽ tranh bằng đồ họa máy tính nhé.

A B C D M N
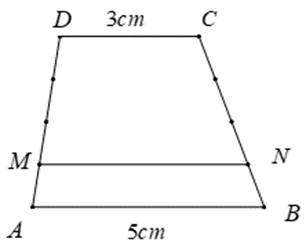
Hai tg ACD và tg ABC có đường cao từ A->CD = đường cao từ C->AB nên
\(\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{CD}{AB}=\dfrac{3}{5}\)
\(S_{ABCD}=S_{ACD}+S_{BCD}\)
\(\Rightarrow S_{ACD}=\dfrac{3}{3+5}xS_{ABCD}=\dfrac{3}{8}xS_{ABCD}=\dfrac{3}{8}x16=6cm^2\)
\(\Rightarrow S_{ABC}=S_{ABCD}-S_{ACD}=16-6=10cm^2\)
Hai tg ACD và tg BCD có đường cao từ A->CD = đường cao từ B->CD và chung cạnh CD
\(\Rightarrow S_{ACD}=S_{BCD}=6cm^2\)
C/m tương tự ta cũng có
\(S_{ABC}=S_{ABD}=10cm^2\)
Hai tg ABN và tg ABC có chung đường cao từ A->BC nên
\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{BN}{BC}=\dfrac{1}{4}\Rightarrow S_{ABN}=\dfrac{1}{4}xS_{ABC}=\dfrac{1}{4}x10=2,5cm^2\)
đường cao từ N->AB là
\(\dfrac{2xS_{ABN}}{AB}=\dfrac{2x2,5}{5}=1cm\)
Hai tg NCD và tg BCD có chung đường cao từ D->BC nên
\(\dfrac{S_{NCD}}{S_{BCD}}=\dfrac{CN}{BC}=\dfrac{3}{4}\Rightarrow S_{NCD}=\dfrac{3}{4}xS_{BCD}=\dfrac{3}{4}x6=4,5cm^2\)
\(S_{ADN}=S_{ABCD}-S_{ABN}-S_{CDN}=16-2,5-4,5=9cm^2\)
Hai tg AMN và tg ADN có chung đường cao từ N->AD nên
\(\dfrac{S_{AMN}}{S_{ADN}}=\dfrac{AM}{AD}=\dfrac{1}{4}\Rightarrow S_{AMN}=\dfrac{1}{4}xS_{ADN}=\dfrac{1}{4}x9=2.25cm^2\)
\(S_{ABNM}=S_{ABN}+S_{AMN}=2,5+2,25=4,75cm^2\)
Như vậy ta biết diện tích hình thang ABNM, biết đáy lớn AB, biết đường cao (đường cao từ N->AB). Áp dụng công thức tính diện tích hình thang sẽ tính được đáy nhỏ MN.
Bạn tự tính nốt nhé

Đổi 1kg = 1000 g.
a) Tổng số tiền mẹ đưa cho Trang là:
50 000 x 2 + 20 000 + 5 000 = 125 000 ( đồng )
Số tiền mua thịt bò là:
300 000 : 1000 x 300 = 90 000 ( đồng )
Số tiền mua bông cải xanh là:
30 000 : 1000 x 500 = 15 000 ( đồng )
Tổng số tiền mua hàng là:
90 000 + 15 000 + 5 000 = 110 000 ( đồng )
Vì 110 000 < 125 000 nên ⇒ Bạn Trang đủ tiền mua hàng.
b) Số tiền bạn Trang cầm về là:
125 000 - 110 000 = 15 000 ( đồng )
Nhưng cửa hàng lại không có mệnh giá tiền dưới 10 000 đồng, nên cửa hàng chắc chắn phải đi đổi tiền.
Bạn Trang sẽ cầm về những mệnh giá tiền là : 1 tờ 10 000 đồng và 1 tờ 5 000 đồng.
Bạn Trang sẽ cầm về những mệnh giá tiền là : 1 tờ 10 000 đồng và 1 tờ 5 000 đồng.

HD:
Coi bài là 2 chuyển động ngược chiều gặp nhau
Ngày hôm trước là vật chuyển động 1 và ngày hôm sau là vật chuyển động 2

b) Xét phương trình 2 có
(1-x2 )/(1+xy)2 - (x+y)2 - y2 =1
=>(1-x2)/1+2xy+x2y2-x2-2xy-y2 -y2=1
=>(1-x2) /(1-x2 )-y2(1-x2) -y2 =1
=>(1-x2)/(1-x2)(1-y2) -y2=1
=>1/(1-y2) -y2=1
=>1=(1-y2)2
=>1=1-2y2+y4
=>y4-2y2=0
=>y2(y2-2)=0
=>y=0
y2-2=0
=> y=+√2
=> y=-√2
Thay y vào phương trình 1 là ra x
à nhầm ... sửa lại dòng 6
=> 1/(1-y2) - y2=1
=> 1/(1-y2)=1+y2
=> 1=1-y4
=> y=0
=>x=3
=> x=-3

Để chứng minh rằng một đa giác lồi có n cạnh, khi được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau, thì n phải chia hết cho 3, ta có thể sử dụng phương pháp quy nạp (induction) để giải quyết bài toán này.
Đầu tiên, chúng ta xét trường hợp đơn giản nhất khi n = 3, tức là đa giác là tam giác. Trong trường hợp này, không cần vẽ đường chéo nào cả, vì tam giác đã được chia thành các tam giác bằng nhau. Và n = 3 chia hết cho 3.
Giả sử đa giác có n cạnh thỏa mãn điều kiện trong đề bài. Ta sẽ chứng minh rằng khi thêm một cạnh mới vào đa giác, tức là n+1 cạnh, thì n+1 cũng phải chia hết cho 3.
Giả sử đa giác có n cạnh và đã được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau. Khi thêm một cạnh mới vào đa giác, chúng ta sẽ thêm một tam giác mới và tạo ra một đường chéo mới. Khi đó, số tam giác trong đa giác tăng thêm một đơn vị và số đường chéo tăng thêm một đơn vị.
Điều quan trọng là ta phải đảm bảo rằng khi thêm một cạnh mới vào, chúng ta vẫn có thể chia đa giác thành các tam giác bằng nhau bằng cách vẽ n-2 đường chéo đôi một không cắt nhau. Điều này có nghĩa là ta cần thêm một đường chéo mới để duy trì tính chất của đa giác ban đầu.
Với việc thêm một cạnh mới, số đường chéo tăng lên một đơn vị, nên ta cần có (n-2)+1 = n-1 đường chéo. Điều này đồng nghĩa với việc n-1 phải chia hết cho 3.
Dựa trên quy nạp, chúng ta có thể kết luận rằng với mọi số tự nhiên n ≥ 3, nếu đa giác có n cạnh và được chia thành các tam giác bằng nhau bằng cách vẽ n-3 đường chéo đôi một không cắt nhau, thì n phải chia hết cho 3.
Vậy, điều phải chứng minh đã được chứng minh.