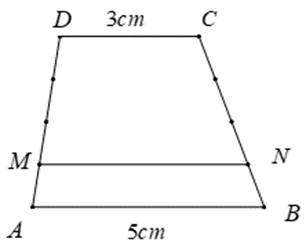
Cho hình thang ABCD có độ dài đáy AB=5cm; CD=3cm. Các điểm M, N lần lượt nằm trên các cạnh AD và BC sao cho MA= 1/4 AD, NB= 1/4BC. Nối M với N, ta được hai hình thang ABNM và CDMN. S của ABCD =16cm2. Tính độ dài MN.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 1kg = 1000 g.
a) Tổng số tiền mẹ đưa cho Trang là:
50 000 x 2 + 20 000 + 5 000 = 125 000 ( đồng )
Số tiền mua thịt bò là:
300 000 : 1000 x 300 = 90 000 ( đồng )
Số tiền mua bông cải xanh là:
30 000 : 1000 x 500 = 15 000 ( đồng )
Tổng số tiền mua hàng là:
90 000 + 15 000 + 5 000 = 110 000 ( đồng )
Vì 110 000 < 125 000 nên ⇒ Bạn Trang đủ tiền mua hàng.
b) Số tiền bạn Trang cầm về là:
125 000 - 110 000 = 15 000 ( đồng )
Nhưng cửa hàng lại không có mệnh giá tiền dưới 10 000 đồng, nên cửa hàng chắc chắn phải đi đổi tiền.
Bạn Trang sẽ cầm về những mệnh giá tiền là : 1 tờ 10 000 đồng và 1 tờ 5 000 đồng.
Bạn Trang sẽ cầm về những mệnh giá tiền là : 1 tờ 10 000 đồng và 1 tờ 5 000 đồng.

HD:
Coi bài là 2 chuyển động ngược chiều gặp nhau
Ngày hôm trước là vật chuyển động 1 và ngày hôm sau là vật chuyển động 2

b) Xét phương trình 2 có
(1-x2 )/(1+xy)2 - (x+y)2 - y2 =1
=>(1-x2)/1+2xy+x2y2-x2-2xy-y2 -y2=1
=>(1-x2) /(1-x2 )-y2(1-x2) -y2 =1
=>(1-x2)/(1-x2)(1-y2) -y2=1
=>1/(1-y2) -y2=1
=>1=(1-y2)2
=>1=1-2y2+y4
=>y4-2y2=0
=>y2(y2-2)=0
=>y=0
y2-2=0
=> y=+√2
=> y=-√2
Thay y vào phương trình 1 là ra x
à nhầm ... sửa lại dòng 6
=> 1/(1-y2) - y2=1
=> 1/(1-y2)=1+y2
=> 1=1-y4
=> y=0
=>x=3
=> x=-3

Một mảnh đất hình chữ nhật có chiều dài là 30, chều rộng bằng 1/3.
Trên mảnh vườn đó trồng khoai. Cứ 10 m2 thì được 50 kg khoai.Hỏi diện tích và số kg khoai
Chiều rộng mảnh vườn là:
30*1/3=10(m)
diện tích mảnh vườn đó là:
30*10=300(m2)
số kg khoai thu đc là:
300:10*50=1500kg=1,5 tấn

\(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+3y^3=2023\)
\(\Leftrightarrow\left[\left(x+1\right)\left(x+7\right)\right]\left[\left(x+3\right)\left(x+5\right)\right]+3y^3=2023\)
\(\Leftrightarrow\left(x^2+8x+7\right)\left(x^2+8x+15\right)+3y^3=2023\) (*)
Đặt \(x^2+8x+11=t\left(t\inℤ;t\ge-5\right)\), pt (*) trở thành \(\left(t-4\right)\left(t+4\right)+3y^3=2023\)
\(\Leftrightarrow t^2-16+3y^3=2023\)
\(\Leftrightarrow t^2+3y^3=2039\) (1)
Xét pt (1), dễ thấy \(t^2\equiv0\left(mod3\right)\) hoặc \(t^2\equiv1\left(mod3\right)\), lại có \(3y^3\equiv0\left(mod3\right)\) nên \(VT\equiv0\left(mod3\right)\) hoặc \(VT\equiv1\left(mod3\right)\). Nhưng \(VP=2039\equiv2\left(mod3\right)\), điều này có nghĩa là (1) vô nghiệm.
Vậy phương trình đã cho không thể có nghiệm nguyên.
(x+1)(x+3)(x+5)(x+7)+3y3=2023
⇔[(�+1)(�+7)][(�+3)(�+5)]+3�3=2023⇔[(x+1)(x+7)][(x+3)(x+5)]+3y3=2023
⇔(�2+8�+7)(�2+8�+15)+3�3=2023⇔(x2+8x+7)(x2+8x+15)+3y3=2023 (*)
Đặt �2+8�+11=�(�∈Z;�≥−5)x2+8x+11=t(t∈Z;t≥−5), pt (*) trở thành (�−4)(�+4)+3�3=2023(t−4)(t+4)+3y3=2023
⇔�2−16+3�3=2023⇔t2−16+3y3=2023
⇔�2+3�3=2039⇔t2+3y3=2039 (1)
Xét pt (1), dễ thấy �2≡0(���3)t2≡0(mod3) hoặc �2≡1(���3)t2≡1(mod3), lại có 3�3≡0(���3)3y3≡0(mod3) nên ��≡0(���3)VT≡0(mod3) hoặc ��≡1(���3)VT≡1(mod3). Nhưng ��=2039≡2(���3)VP=2039≡2(mod3), điều này có nghĩa là (1) vô nghiệm.
Vậy phương trình đã cho không thể có nghiệm nguyên
A B C D M N
Hai tg ACD và tg ABC có đường cao từ A->CD = đường cao từ C->AB nên
\(\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{CD}{AB}=\dfrac{3}{5}\)
\(S_{ABCD}=S_{ACD}+S_{BCD}\)
\(\Rightarrow S_{ACD}=\dfrac{3}{3+5}xS_{ABCD}=\dfrac{3}{8}xS_{ABCD}=\dfrac{3}{8}x16=6cm^2\)
\(\Rightarrow S_{ABC}=S_{ABCD}-S_{ACD}=16-6=10cm^2\)
Hai tg ACD và tg BCD có đường cao từ A->CD = đường cao từ B->CD và chung cạnh CD
\(\Rightarrow S_{ACD}=S_{BCD}=6cm^2\)
C/m tương tự ta cũng có
\(S_{ABC}=S_{ABD}=10cm^2\)
Hai tg ABN và tg ABC có chung đường cao từ A->BC nên
\(\dfrac{S_{ABN}}{S_{ABC}}=\dfrac{BN}{BC}=\dfrac{1}{4}\Rightarrow S_{ABN}=\dfrac{1}{4}xS_{ABC}=\dfrac{1}{4}x10=2,5cm^2\)
đường cao từ N->AB là
\(\dfrac{2xS_{ABN}}{AB}=\dfrac{2x2,5}{5}=1cm\)
Hai tg NCD và tg BCD có chung đường cao từ D->BC nên
\(\dfrac{S_{NCD}}{S_{BCD}}=\dfrac{CN}{BC}=\dfrac{3}{4}\Rightarrow S_{NCD}=\dfrac{3}{4}xS_{BCD}=\dfrac{3}{4}x6=4,5cm^2\)
\(S_{ADN}=S_{ABCD}-S_{ABN}-S_{CDN}=16-2,5-4,5=9cm^2\)
Hai tg AMN và tg ADN có chung đường cao từ N->AD nên
\(\dfrac{S_{AMN}}{S_{ADN}}=\dfrac{AM}{AD}=\dfrac{1}{4}\Rightarrow S_{AMN}=\dfrac{1}{4}xS_{ADN}=\dfrac{1}{4}x9=2.25cm^2\)
\(S_{ABNM}=S_{ABN}+S_{AMN}=2,5+2,25=4,75cm^2\)
Như vậy ta biết diện tích hình thang ABNM, biết đáy lớn AB, biết đường cao (đường cao từ N->AB). Áp dụng công thức tính diện tích hình thang sẽ tính được đáy nhỏ MN.
Bạn tự tính nốt nhé
Sabcd = 16cm² => (3+5)xHabcd =32 cm => Habcd = 4cm.
Điểm M và N lần lượt = 1/4 AD và BC nên chiều cao ABNM = 4:4 = 1cm. Chiều cao CD đến MN = 4-1= 3cm
Ta có: Sabnm + Smncd = 16cm² => (5+mn)+ (3+mn)x3 = 32cm
4mn+14=32cm => mn=4,5cm