Một hình chữ nhật ABCD có chiều dài AB 7,5m. Chiều rộng AD kém chiều dài là 2,75m. Người ta mở rộng hình chữ nhật bằng cách kéo dài mỗi chiều AB và DC về cùng một phía 2,5m đẻ được hình chữ nhật mới là ADNM. Tính diện tích hình chữ nhật ADMN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


200m trồng được số cây là:
200:2=100(cây)
Vì 2 đầu đoạn đường đều có cây nên các cụ trồng được số cây là :
100+2=102(cây)
Đ/S:102 cây

2x2 + 3x - 1 chia hết cho x + 1 nên x có thể là số nào cũng được :)

lấy phương trình trên trừ đi phương trình dưới ta có
\(\overline{abc}-\overline{cba}=n^2-1-\left(n-2\right)^2=4n-5\)
\(\Leftrightarrow99a-99c=4n-5=4\left(n-26\right)+99\)
rõ ràng a,c phải khác 0 thì abc và cba mới là số tự nhiên
do vế trái chia hết cho 99 nên vế phải cũng phải chia hết cho 99 , do đó tồn tại số tự nhiên k sao cho
\(\Rightarrow n-26=99k\)\(\Rightarrow99\left(a-c\right)=99\left(4k+1\right)\)
mà a và c là hai chữ số khác không nên hiệu a-c nằm trong tập {-8,8}
\(\Rightarrow k\in\left\{-2;-1;0;1\right\}\)từ đó ta tìm được \(n\in\left\{-172;-73;26;125\right\}\)
mà n là số tự nhiên lớn hơn 2 vậy nên \(\orbr{\begin{cases}n=26\\n=125\end{cases}}\Rightarrow\orbr{\begin{cases}\overline{abc}=26^2-1=675\\\overline{abc}=125^2-1=15624\end{cases}}\)
do abc là số có 3 chứ số nên chỉ có 675 lầ thỏa mãn đề
\(\hept{\begin{cases}\overline{abc}=100a+10b+c=n^2-1\left(1\right)\\\overline{cba}=100c+10b+a=n^2-4n+4\left(2\right)\end{cases}}\)
từ 1 zà 2 \(=>99\left(a-c\right)=4n-5=>4n-5⋮99\)
Mặt khác \(100\le n^2-1\le999\Leftrightarrow101\le n^2\le1000=>11\le n\le31\Leftrightarrow39\le4n-5\le119\)
từ 3 zà 4 => 4n-5=99 => n=26
zậy số cần tim là abc=675

ta có \(x+y+z=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{xy+yz+xz}{xyz}\)
hay \(xy+yz+xz=x+y+z\)do xyz=1 nên PT tương đương
\(xyz-xy-yz-xz+y+y+z-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(yz-y-z+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(y-1\right)\left(z-1\right)=0\)\(\Rightarrow\)hoăc x=1 hoặc y=1 hoặc z=1
xét x=1 ta có P=0
tương tự với y và z ta đều có P=0
Vậy P=0

a) ABCD là hcn => AB//CD; AB=CD ; AD=BC
mà AF//CK
=> AKCF là hbh
=> AF=CK
=. tam giác ADE= tam giác CBK ( ch-gcz)
b) M là trung điểm của AE ; MN//AD
=> MN là đường trung bình của tam giác ADE
=> MN=1/2AD
BC//AD , BC=AD; Q là trung điểm của BC nên BQ//AD; BQ=1/2AD
=> MN//BQ zà MN=BQ=> MNBQ là hbh
=> góc NMB = góc NQB
c) góc AQN = góc BQN - góc BQA=góc BMN -(90độ - góc QAB)
=góc QAB +góc BMN-90 độ
ta có góc BMN = góc BME +NME = góc MAB +MBA+ADE
=> BMN=MBA+ 90 đô
=> góc AQN=QAB+MBA+90 độ - 90độ=QAB+MBA(1)
tam giác AED ~ tam giác BEA (g-g)
=> AD/BA=DE/AE=2DN/2MA=DN/MA
=> tam giác AMB ~ tam giác DNA (c-g-c)
=> góc ABM = góc DAN (2)
từ 1 zà 2 => dpcm

\(ĐK:x\inℝ\)
Nếu x < 0 thì \(2x+\sqrt{x^2+5}< \sqrt{x^2+5}< \sqrt{x^2+12}< \sqrt{x^2+12}+3\)
Trường hợp này phương trình vô nghiệm nên \(x\ge0\)
\(\sqrt{x^2+12}+3=\sqrt{x^2+5}+2x\)
\(\Leftrightarrow\left(\sqrt{x^2+12}-4\right)-\left(\sqrt{x^2+5}-3\right)+\left(4-2x\right)=0\)\(\Leftrightarrow\frac{\left(x+2\right)\left(x-2\right)}{\sqrt{x^2+12}+4}-\frac{\left(x+2\right)\left(x-2\right)}{\sqrt{x^2+5}+3}-2\left(x-2\right)=0\)\(\Leftrightarrow\left(x-2\right)\left(\frac{x+2}{\sqrt{x^2+12}+4}-\frac{x+2}{\sqrt{x^2+5}+3}-2\right)=0\)
Ta có: \(\frac{x+2}{\sqrt{x^2+12}+4}-\frac{x+2}{\sqrt{x^2+5}+3}-2=\left(x+2\right)\left(\frac{1}{\sqrt{x^2+12}+4}-\frac{1}{\sqrt{x^2+5}+3}\right)-2\)\(=\left(x+2\right)\frac{\sqrt{x^2+5}-\sqrt{x^2+12}-1}{\left(\sqrt{x^2+12}+4\right)\left(\sqrt{x^2+5}+3\right)}-2< 0\forall x\ge0\)nên x - 2 = 0 hay x = 2
Vậy nghiệm duy nhất của phương trình là 2
\(\sqrt{x^2+12}+3=\sqrt{x^2+5}+2x\)
\(\Leftrightarrow\sqrt{x^2+12}-\sqrt{x^2+5}=2x-3\)
bình phương 2 vế ta được :
\(\Leftrightarrow2x^2+17-2\sqrt{\left(x^2+12\right)\left(x^2+5\right)}=4x^2-12x+9\)
\(\Leftrightarrow-2\sqrt{\left(x^2+12\right)\left(x^2+5\right)}=2x^2-12x-8\)
hay : \(4\left(x^2+12\right)\left(x^2+5\right)=4\left(x^2-6x-4\right)^2\)
\(\Leftrightarrow\left(x^2+12\right)\left(x^2+5\right)=\left(x^2-6x-4\right)^2\)
\(\Leftrightarrow x^4+17x^2+60-\left(x^2-6x-4\right)^2=0\)
\(\Leftrightarrow x=2\)
Vậy x = 2

Bài giải
Nhà Lan bằng một phần nhà Nhi là :
40:8 = 5 ( phần )
Đáp số 5 phần
Vậy = 1 / 5 nhà Nhi
bài giải
Nhà Lan bằng một phần nhà Nhi là :
40 : 8 = 5 ( phần )
Đáp số : 5 phần

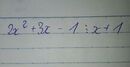
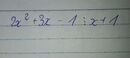
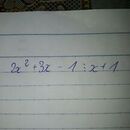
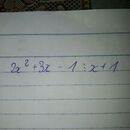
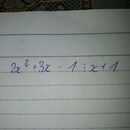

Chiều rộng hình chữ nhật ABCD là : 7,5 - 2,75 = 4,75 ( m )
Chiều dài hình chữ nhật ADMN là : 7,5 + 2,5 = 10 ( m )
Chiều rộng hình chữ nhật ADMN là : 4,75 + 2,5 = 7,25 ( m )
Diện tích hình chữ nhật ADMN là : 10 * 7,25 = 72,5 ( m2 )
Đ/s : 72,5m2