TIPS HỌC TOÁN DÀNH CHO BN HỌC KO HIỂU ,ÍT HỌC TOÁN !

1.BÀI TẬP NÀO KO HIỂU ,hỏi thầy cô, anh chị ,bạn bè

2.KO dấu dốt 

3.Học TOÁN mỗi ngày 

4.ko cần học quá sức ,người giỏi luôn biết sắp xếp thời gian học 

5.Yêu thích TOÁN 

6.Ôn lại bài cũ ,phải học thuộc lý thuyết ở lớp ,rồi mới làm bài tập

7.Học có mục đích 

8.làm btvn mà ko hiểu thì có thể chia sẻ (ví dụ như mình)

CHÚC CÁC BN HỌC TỐT TOÁN HƠN

     Cô Thương Hoài thân ái, chào tất cả các em học viên của olm.vn.

Vậy là đã gần một tháng kể từ khi cô phát động sự kiện: lên olm.vn review kết quả các năm học. Đây là cuộc thi có tên:

                 HỌC CÙNG OLM MỖI NGÀY HỌC GIỎI HỌC HAY

Chắc là các em đang mong ngóng kết quả cuộc thi lắm rồi phải không?

Vậy hôm nay cô xin thông báo kết quả chính thức nhé. Các em mau vào xem có tên mình không nha. Chúc tất cả các em may mắn.

                    I, MỤC ĐÍCH CUỘC THI:

                        Cuộc thi nhằm khuyến khích tinh thần học tập của các em học sinh trên olm, giúp các em cố gắng, nỗ lực rèn luyện thành tài. Tạo cho các em môi trường học vừa thân thiện, vừa năng động, vừa hấp dẫn, cũng như ghi nhận sự nỗ lực của các em trong suốt quá trình học tập. Tăng thêm sự yêu mến của các em đối với hệ thống, từ đó nâng cao chất lượng học của các em, tạo sự tin tưởng đối với phụ huynh khi hệ thống có nhiều học sinh đạt thành tích cao theo học.

               II, BAN TỔ CHỨC:

1, Trưởng ban tổ chức, chủ trì và trao giải cuộc thi Thầy: Hà Đức Thọ

2, Chỉ đạo cuộc thi Cô: Nguyễn Thúy Hòa

3, Quản lí, gám sát, sáng lập cuộc thi cô: Nguyễn Thị Thương Hoài

4, Thiết kế giấy khen cô Chang Thỏ

5, Nguồn kinh phí: Olm

               III, Danh Sách Thí Sinh Đoạt giải

  1, Giải Chính: Thầy Hà Đức Thọ trao giải, giải gồm giấy chứng nhận đóng giấu đỏ và có chữ ký của Thầy Hà Đức Thọ. Kèm hiện vật.

Giải Phụ: Cô Thương Hoài trao giải.

 a, Học viên olm có thành tích xuất sắc trong học tập và có nhiều đóng góp tích cực cho cộng đồng.

b, Giải bình luận sớm nhất cho cuộc thi:

c, Giải cho người tham gia.

Chú ý: Cô là người duy nhất phụ trách trao giải cho những em đạt giải thưởng phụ. Đồng thời, cô cũng chỉ có duy nhất một tài khoản trên olm với link cá nhân sau:

https://olm.vn/thanhvien/1655474456545.

Nếu bất cứ ai ngoài cô yêu cầu các em có tên trong danh sách cung cấp thông tin cá nhân để nhận giải đều là lừa đảo. Trong vòng 30 ngày kể từ khi có thông báo này, các em có tên trong danh sách giải thưởng phụ không liên lạc với cô để nhận giải thì coi như em đã từ chối giải thưởng

                 IV, Lời kết: 

Trên đây là toàn bộ thông báo kết quả cuộc thi do cô sáng lập và cùng các thầy cô trong ban tổ chức triển khai.

Cô chân thành cảm ơn các em đã tham gia nhiệt tình, chân thành, trung thực, tất cả các em đều rất xứng đáng được nhận được giải nhưng số lượng giải có hạn. 
Chỉ có thể trao cho những bạn có thành tích cao nhất. Chúc các em có nhiều kỉ niệm đẹp về cuộc thi và hẹn gặp lại các em trong các cuộc thi mới. Chúc các em học tập thật vui vẻ và hiệu quả trên olm. Giờ các bạn có tên trong danh sách giải thưởng đâu nhỉ? 
Cô muốn nhìn thấy cánh tay của các em giơ lên tại cmt.

                                           Thân mến!

                            Thay mặt ban tổ chức: Cô Thương Hoài

1. Cho bàn cờ 8x8 và 16 quân tốt (8 đen, 8 trắng) như trong hình. Hai người chơi, mỗi người cầm 1 loại quân (trắng/ đen). Quân trắng luôn đi trước, sau đó luân phiên. Biết rằng luật cờ vua được bảo toàn, tuy nhiên không được có sự ăn quân nào. Nếu bên nào đi 1 nước làm cho bên kia không thể thực hiện nước đi nào hợp lệ thì sẽ là người thắng cuộc. Hỏi có người chơi nào có chiến lược thắng hay không? Nếu có, hãy mô tả và giải thích chiến lược đó.

 2. Cho bàn cờ kích thước \(n\times n\). Hỏi 1 quân mã xuất phát từ 1 ô góc của bàn cờ đến góc đối diện thì cần ít nhất bao nhiêu nước đi? (Biết rằng quân mã đi như mã trong cờ vua)

 3. Tìm số quân tượng lớn nhất có thể đặt vào bàn cờ vua 8x8 sao cho không quân tượng nào tấn công quá 3 quân tượng khác (tượng tấn công như trong cờ vua, đi chéo vô hạn và không tấn công xuyên thấu, quan hệ tấn công là 2 chiều)

 4. Có bao nhiêu cách đặt 8 quân xe lên bàn cờ sao cho không có 2 quân xe nào ăn nhau và không có quân xe nào ở vị trí cấm được đánh dấu là vòng tròn màu xanh lục như hình vẽ: 

 Một hành lang có 100 cánh cửa được đánh số 1,2,...,100 và có một người đi qua hành lang đó. Ban đầu, tất cả 100 cánh cửa đều đóng. Ở lần đi thứ nhất, người đó thay đổi trạng thái đóng/mở của tất cả các cửa. Ở lần đi thứ hai, người đó thay đổi trạng thái đóng/mở của tất cả các cửa có số là bội của 2. Cứ như thế, ở lần đi thứ \(k\left(1\le k\le100\right)\), người đó thay đổi trạng thái đóng/mở của tất cả các cửa có số là bội của \(k\). Hỏi sau lần đi thứ 100, những cánh cửa có số mấy sẽ ở trạng thái mở?

          LÊN OlM.VN CÙNG REVIEW KẾT QUẢ HỌC TẬP CỦA CÁC EM TẠI ĐÂY VÀ NHẬN NGAY PHẦN THƯỞNG CỦA CÔ THƯƠNG HOÀI NHÉ CÁC EM

        Cô Thương Hoài thân ái chào tất cả các em học viên của olm.vn! olm.vn hệ thống giáo dục trực tuyến hàng đầu và thịnh hành nhất hiện nay.

Một mùa hè thú vị đã sắp qua rồi, các em lại háo hức chuẩn bị cho một năm học mới và tất bật với sách vở để đến trường gặp lại thầy, gặp lại cô, gặp lại những bạn bè thân yêu. Cô băn khoăn tự hỏi không biết khi các em bận học như vậy, lúc đó các em có còn nhớ đến những kỉ niệm đẹp đẽ trên olm cùng bạn bè, cùng cô Thương Hoài không nữa. Và Để các em có những kỉ niệm đẹp trên olm, hôm nay cô sẽ cho các em cơ hội nhận thưởng gp và một số thẻ cào điện thoại các nhà mạng, thông qua việc các em cùng cô review kết quả học tập các em năm học 2022 - 2023.

           I, Cách thức tham gia, các em chụp ảnh giấy khen ví dụ học sinh giỏi, giấy chứng nhận đoạt giải, nếu có và đăng vào phần bình luận. Cô sẽ xem xét kết quả học tập đó để trao giải. 

 II, Cơ cấu thưởng như sau: 

         1, Tất cả các bình luận ( không vi phạm tiêu chuẩn cộng đồng đều được thưởng 2gp + 1 sp

          2, Đối với những bạn có thành tích cao sẽ được thưởng thêm 5 gp

         3, Cô sẽ chọn ra 5 bạn có thành tích cao nhất để trao giải bằng thẻ cào điện thoại

                  +    1, Giải nhất thẻ cào 100k

                 +     1, Giải nhì thẻ cào 50 k

                 +      1, Giải ba thẻ cào 30 k

                  +     2, giải khuyến khích thẻ cào 20 k 

               III, Thời hạn kết thúc 24h 20/8/ 2023

               IV, cô sẽ công bố danh sách các bạn doạt giải vào ngày 21/8/2023, sau đó các bạn liên lạc với cô qua nhắn tin trên olm để nhận giải.

                                                         Bây giờ cô xin phép bắt đầu nhé các em. Và cô sẽ bắt đầu từ các bạn học sinh của cô.

               Bạn ở vị trí số 1: 

                Họ và tên : Vũ Thị Minh Ngọc. l 

                Giải khuyến khích violympic cấp quốc qia 

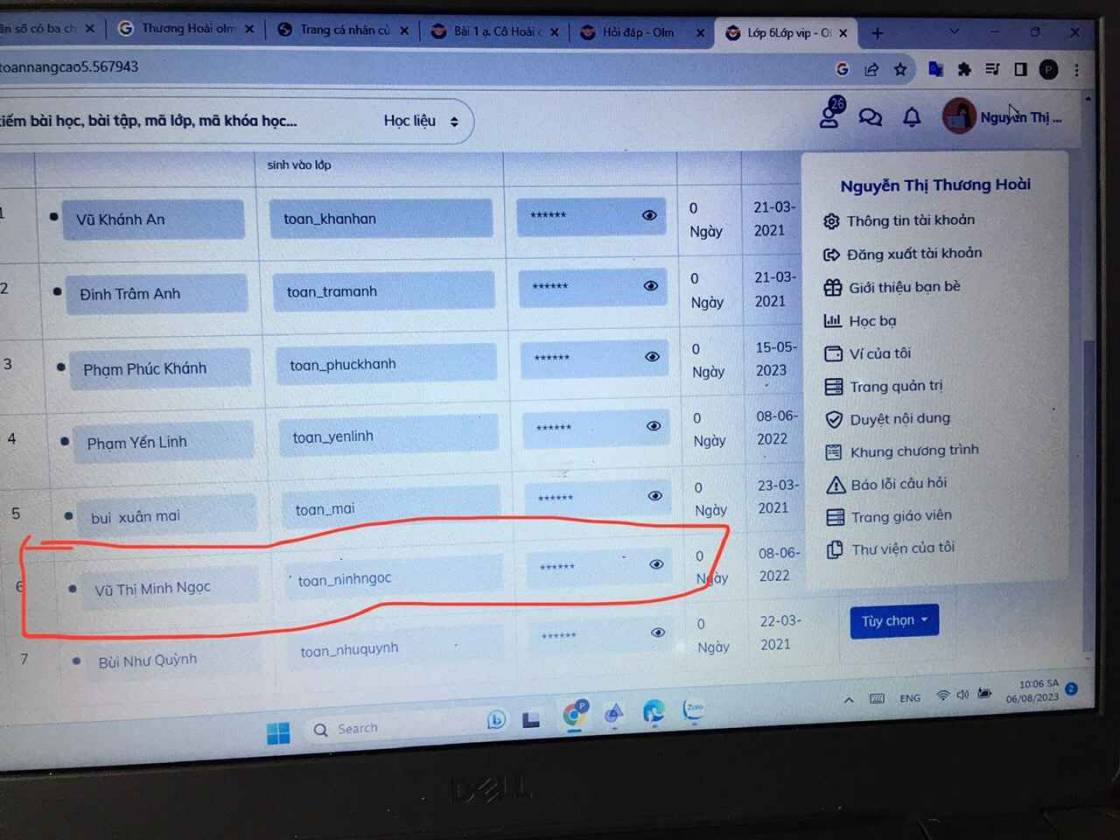
Bạn ở vị trí số 2:

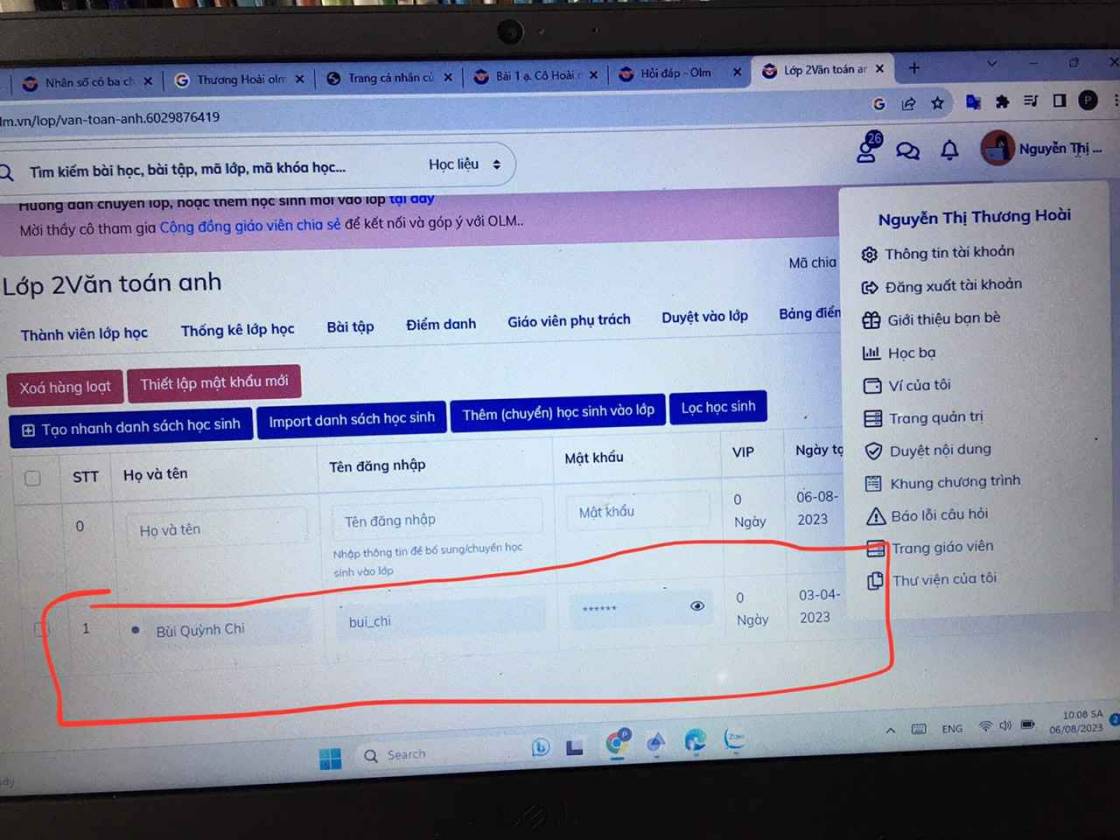
Họ Và Tên: Bùi Quỳnh Chi 

Giải khuyến khích vioedu cấp tỉnh. Bạn này rất chịu khó học và làm bài tập cô Thương Hoài giao. Bạn còn giỏi tiếng trung vì mẹ bạn dạy tiếng trung. Đặc biệt bạn rất tự giác học và luyện trên olm các em ah. 

Vị trí số ba Lại Ngọc Hà: bạn này thường hay hỏi cô môn toán và rất chịu khó học trên olm môn tiếng anh

Giải Nhất môn tiếng anh học sinh giỏi cấp huyện: (do bây giờ bạn đi vắng nên cô chưa lấy được file ảnh giấy khen)

Vị trí số 4: Bùi Như Quỳnh

Năm ngoái Huy chương vàng cấp tỉnh môn toán

Năm nay Giải ba Học sinh giỏi toán cấp huyện

Trên đây là một số các bạn học sinh là học sinh của cô và cũng học trên olm.vn. Như vậy chứng tỏ chất lượng của giáo viên olm là rất chuẩn nhé.

Cô rất mong nhận được sự chia sẻ từ các em, làm cho diễn đàn olm trở nên sôi động, tích cực và là nơi các em giao lưu với cộng đồng tri thức cả nước.

     Nhanh tay để lại bình luận nào các em. Bạn bình luận đầu tiên trên olm sẽ nhận được thẻ cào 10 k.

          Lời kết cuối cùng cô chúc các em thật nhiều sức khỏe, mạnh khỏe, học tập và nỗ lực hết mình để có những thành quả cao hơn trong năm tới .

 1. Tìm tất cả các đa thức \(P\left(x\right)\) khác đa thức 0 thỏa mãn \(P\left(2014\right)=2046\) và \(P\left(x\right)=\sqrt{P\left(x^2+1\right)-33}+32,\forall x\ge0\)

 2. Tìm tất cả các đa thức \(P\left(x\right)\inℤ\left[x\right]\) bậc \(n\) thỏa mãn điều kiện sau: \(\left[P\left(2x\right)\right]^2=16P\left(x^2\right),\forall x\inℝ\)

 Với mọi \(m\inℤ^+\), ta kí hiệu \(\sigma\left(n\right)\) là tổng các ước nguyên dương của \(n\) (bao gồm cả chính nó).

 a) Chứng minh rằng, nếu \(\sigma\left(n\right)\) là số lẻ thì \(n=2^r.l^2\) với \(r,l\inℕ\), trong đó \(l\) là số lẻ.

 b)  Số tự nhiên \(n\) được gọi là "hoàn hảo" khi và chỉ khi \(\sigma\left(n\right)=2n\). CMR nếu \(n\) là số hoàn hảo chẵn thì \(n=2^{m-1}\left(2^m-1\right)\) với \(m\inℕ,m\ge2\) sao cho \(2^m-1\) là số nguyên tố.

 Xét dãy số \(\left\{x_n\right\}^{+\infty}_{n=1}\) như sau: \(x_1=1\) và với mọi \(n=1,2,...\) thì 

\(x_{n+1}=\dfrac{\left(2+\cos\alpha\right)x_n+\cos^2\alpha}{\left(2-2\cos2\alpha\right)x_n+2-2\cos2\alpha}\),

trong đó \(\alpha\) là một tham số thực. Tìm tất cả các giá trị của \(\alpha\) để dãy số \(\left\{y_n\right\}\), với \(y_n=\sum\limits^n_{k=1}\dfrac{1}{2x_k+1},\forall n=1,2,...\) có giới hạn hữu hạn khi \(n\rightarrow+\infty\). Hãy tìm giới hạn của dãy số \(\left\{y_n\right\}\) trong các trường hợp đó.