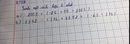Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A không hề chia hết cho 2 hay 30 nhé bạn, đơn giản vì A là số lẻ thôi.
chứng minh chia hết cho 3:
ta có \(A=\left(1+2\right)+\left(2^2+2^3\right)+...+\left(2^{2018}+2^{2019}\right)\)
\(\Leftrightarrow A=3+3\cdot2^2+3\cdot2^4+..+3\cdot2^{2018}\)do đó A chia hết cho 3.
hoàn toàn tương tự ta có
\(A=\left(1+2+2^2\right)+\left(2^3+2^4+2^5\right)+..+\left(2^{2016}+2^{2017}+2^{2018}\right)+2^{2019}\)
\(\Leftrightarrow A=7+7\cdot2^3+7\cdot3^6+..+7\cdot2^{2016}+2^{2019}\)
do đó A cũng không chia hết cho 7 .

Gợi ý cả 2 bài: cách 1 làm rút về đơn vị; cách 2 làm tìm tỉ số.



áp dụng công thức diện tích tam giác ta có
\(S=\frac{abc}{4R}=\frac{r\left(a+b+c\right)}{2}\Rightarrow\frac{3}{2Rr}=\frac{3\left(a+b+c\right)}{abc}\)
vì vậy ta cần chứng minh
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\sqrt{\frac{3\left(a+b+c\right)}{abc}}=\sqrt{3\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)}\)
bình phương hai vế ta có:
\(\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2\ge3\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)\)
\(\Leftrightarrow\left(\frac{1}{a}-\frac{1}{b}\right)^2+\left(\frac{1}{c}-\frac{1}{b}\right)^2+\left(\frac{1}{a}-\frac{1}{c}\right)^2\ge0\)luôn đúng
dấu bằng xảy ra khi a=b=c