Đến hẹn cô lên minigame cho các bạn đây 😉
👉 Các bạn nhanh tay tham gia tại đây nha https://www.facebook.com/olm.vn
 GIẢI TOÁN THẦN TỐC - BỐC NGAY TIỀN MẶT
GIẢI TOÁN THẦN TỐC - BỐC NGAY TIỀN MẶT 

Game nhỏ nhỏ; Quà xinh xinh dành cho các bạn học sinh nhân dịp chuẩn bị vào năm học mới. Nhanh tay rinh những phần quà siêu to khổng lồ với câu hỏi cực kỳ đơn giản nào!!!!
 CƠ CẤU GIẢI THƯỞNG HOÀNH TRÁNG NHƯ SAU:
CƠ CẤU GIẢI THƯỞNG HOÀNH TRÁNG NHƯ SAU:
- 1 Giải Nhất: Tặng 200.000 đồng + áo OLM + voucher ưu đãi khóa học 20%
- 2 Giải Nhì: Tặng 100.000 đồng + túi Tote OLM + voucher ưu đãi khóa học 20%
- 3 Giải Ba : Tặng 50.000 đồng + móc khóa OLM + voucher ưu đãi khóa học 20%
- 5 Giai Khuyến Khích: Tặng sổ + bút bi OLM + voucher ưu đãi khóa học 20%
💥3 BƯỚC THAM GIA ĐƠN GIẢN
Bước 1: "Li.ke" và "Sh.are" bài post Minigame.
Bước 2: C.o.m.m.e.n.t đáp án minigame và dự đoán số người có cùng câu trả lời như bạnBước 3: Tag tên 2 người bạn bất kỳ vào chơi cùng(Ví dụ: 56 - 123 @abc @xyz)
👉 THỂ LỆ TRAO GIẢI THƯỞNG
- Kết quả dựa trên: Đáp án Minigame và số người có cùng câu trả lời đúng như bạn.
- Nếu trường hợp "ĐÁP ÁN" giống nhau, BTC sẽ ưu tiên các bạn có dự đoán gần đúng số người có cùng câu trả lời như bạn.
- Nếu trường hợp "ĐÁP ÁN và DỰ ĐOÁN SỐ NGƯỜI" giống nhau, BTC sẽ ưu tiên bình luận sớm hơn.
📍Lưu ý
- Thực hiện đầy đủ 3 bước trên
- Người chơi có thể tham gia chơi NHIỀU LẦN, càng c.o.m.m.e.n.t nhiều khả năng trúng giải càng cao.
- KHÔNG ĐƯỢC CHỈNH SỬA c.o.m.m.e.n.t
- Mọi hành vi gian lận sẽ không được tính là hợp lệ và BTC sẽ loại khỏi cuộc thi.
- Trong mọi trường hợp, quyết định của BTC là quyết định cuối cùng.
⏰THỜI GIAN
- Minigame diễn ra từ 20h30 ngày 26/07/2023 đến 23h59h ngày 01/08/2023
- Kết quả sẽ được công bố trong ngày 02/08/2023 tại Fanpage OLM https://www.facebook.com/olm.vn
Đừng quên thường xuyên truy cập fanpage OLM để xem những bài giảng, bài tập, phương pháp học tập cực hay các em nhé!




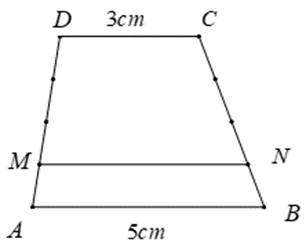
1. Để tìm các đa thức P(x) thỏa mãn điều kiện P(2014) = 2046 và P(x) = P(x^2 + 1) - 33 + 32, ∀x ≥ 0, ta có thể sử dụng phương pháp đệ quy. Bước 1: Xác định bậc của đa thức P(x). Vì không có thông tin về bậc của đa thức, chúng ta sẽ giả sử nó là một hằng số n. Bước 2: Xây dựng công thức tổng quát cho đa thức P(x). Với bậc n đã xác định, ta có: P(x) = a_n * x^n + a_{n-1} * x^{n-1} + ... + a_0 Bước 3: Áp dụng điều kiện để tìm các hệ số a_i. Thay x = 2014 vào biểu thức và giải phương trình: P(2014) = a_n * (2014)^n + a_{n-1} * (2014)^{n-1} + ... + a_0 = 2046 Giải phương trình này để tìm các giá trị của các hệ số. Bước 4: Áp dụng công thức tái lập để tính toán các giá trị tiếp theo của P(x): P(x) = P(x^2+1)-33+32 Áp dụng công thức này lặp lại cho đến khi đạt được kết quả cuối cùng. 2. Để tìm các đa thức P(x) ∈ Z[x] bậc n thỏa mãn điều kiện [P(2x)]^2 = 16P(x^2), ∀x ∈ R, ta có thể sử dụng phương pháp đệ quy tương tự như trên. Bước 1: Xác định bậc của đa thức P(x). Giả sử bậc của P(x) là n. Bước 2: Xây dựng công thức tổng quát cho P(x): P(x) = a_n * x^n + a_{n-1} * x^{n-1} + ... + a_0 Bước 3: Áp dụng điều kiện để tìm các hệ số a_i. Thay x = 2x vào biểu thức và giải phương trình: [P(2x)]^2 = (a_n * (2x)^n + a_{n-1} * (2x)^{n-1} + ... + a_0)^2 = 16P(x^2) Giải phương trình này để tìm các giá trị của các hệ số. Bước 4: Áp dụng công thức tái lập để tính toán các giá trị tiếp theo của P(x): [P(4x)]^2 = (a_n * (4x)^n + a_{n-1} * (4x)^{n-1} + ... + a_0)^2 = 16P(x^2) Lặp lại quá trình này cho đến khi đạt được kết quả cuối cùng.