Cho tam giác ABC nội tiếp (O) ,AB<AC .Ba đường cao AD,BE,CF cắt nhau tại H. N trung điểm BC, đường thẳng vuông góc AB tại A cắt BE tại I, Qua A vẽ đường thẳng // BC cắt EF tại M, MI cắt AH tại T, vẽ AK vuông góc MT tại K. cm: T là trung điểm AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Δ' = b'2 - ac = [-(n-1)]2 - 2n + 3
= n2 - 2n + 1 - 2n + 3
= n2 - 4n + 4 = ( n - 2 )2 ≥ 0 ∀ n
hay pt luôn có nghiệm ∀ n (đpcm)
b) Theo Viète ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2n-2\\x_1x_2=\frac{c}{a}=2n-3\end{cases}}\)
Khi đó P = x12 + x22 = ( x1 + x2 )2 - 2x1x2
= ( 2n - 2 )2 - 2( 2n - 3 )
= 4n2 - 8n + 4 - 4n + 6
= 4n2 - 12n + 10
= ( 2n - 3 )2 + 1 ≥ 1 ∀ n
Dấu "=" xảy ra <=> n = 3/2 . Vậy MinP = 1

a, O là tâm đường tròn nội tiếp nên AO là đường trung trực của tam giác ABC. Tam giác ABC cân tại A nên AO cũng là đường phân giác của góc A.
b, Tamm giác ABK và tam giác ADB có: Góc A chung; AKB = ABD vì chắn hai cung bằng nhau AB và AC. Suy ra tam giác ABK đồng dạng với tam giác ADB. Suy ra\(\frac{AB}{AK}=\frac{AD}{AB}\)suy ra AB2=AD.AK

a, \(\sqrt{\frac{2a}{3}}.\sqrt{\frac{3a}{8}}=\sqrt{\frac{6a^2}{24}}=\sqrt{\frac{a^2}{4}}=\left|\frac{a}{2}\right|=\frac{a}{2}\)
do \(a\ge0\)
b, \(\sqrt{13a}.\sqrt{\frac{52}{a}}=\sqrt{\frac{676a}{a}}=\sqrt{676}=26\)
c, \(\sqrt{5a}.\sqrt{45a}-3a=\sqrt{225a^2}-3a=\left|15a\right|-3a\)
\(=15a-3a=12a\)do a > 0
d, \(=\left(3-a\right)^2-\sqrt{0,2}.\sqrt{180a^2}\)
\(=\left(3-a\right)^2-\sqrt{36a^2}=\left(3-a\right)^2-\left|6a\right|\)
Với \(a\ge0\Rightarrow\left(3-a\right)^2-6a=a^2-6a+9-6a=a^2-12a+9\)
Với \(a< 0\Rightarrow\left(3-a\right)^2+6a=a^2-6a+9+6a=a^2+9\)

Khai phương tích 12.30.40 được:
(A) 1200 ; (B) 120 ; (C) 12 ; (D) 240.
Chọn B
Khai phương tích 12.30.40 (=12.12.10.10) ta được 12.10= 120 (Chọn B)

a
Đường tròn , đường kính có
.
vuông tại có
.
Chứng minh tương tự .
\(\Rightarrow\) .
B
Theo câu a ta có
.
Tam giác và tam giác có chung và .
(c.g.c).
\(\widehat{ACB}\)
c.
Tam giác vuông tại có là trung điểm của
.
cân tại
Theo câu b ta có \(\widehat{AMN}\)
Mà \(\widehat{BAD}\)
\(\widehat{BAD}\)
.
Ta chứng minh vuông tại có
.
Mà
\(\Rightarrow\) là tứ giác nội tiếp.

Xét \(\hept{\begin{cases}4x^2+z^2\ge4xz\\4y^2+z^2\ge4yz\\2x^2+2y^2\ge4xy\end{cases}}\)
\(\Leftrightarrow2\left(3x^2+3y^2+z^2\right)\ge4\left(xy+yz+zx\right)\)
\(\Leftrightarrow3x^2+3y^2+z^2\ge10\)
dấu bằng xảy ra khi và chỉ khi \(x=y=1\)và \(z=2\)

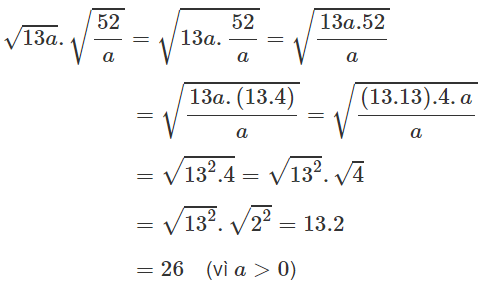

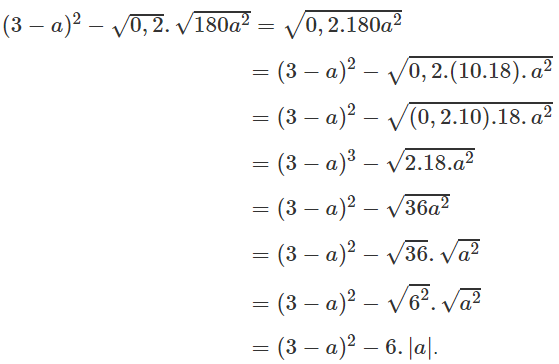
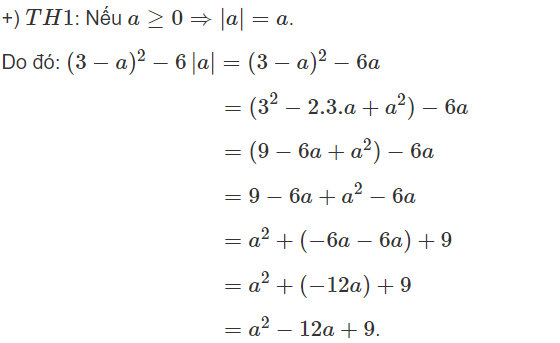
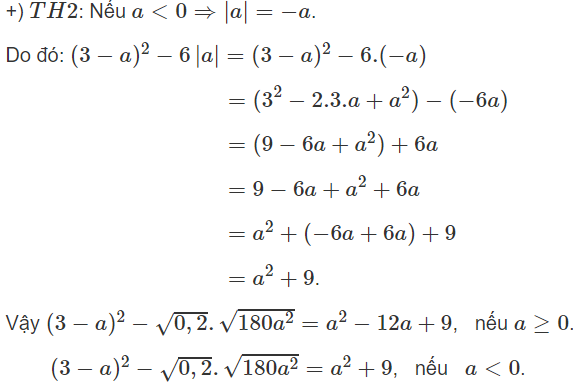
Lấy điểm G trên CF sao cho AG vuông góc với AC.
Ta có ^MAE = ^ACB = ^AFE => AM là tiếp tuyến của (AEF) => \(ME.MF=AM^2\Rightarrow\frac{ME}{MF}=\frac{AM^2}{MF^2}=\frac{AE^2}{AF^2}\)
Áp dụng định lí Thales, ta có: \(\frac{IH}{IE}.\frac{ME}{MF}.\frac{GF}{GH}=\frac{AC}{AE}.\frac{AE^2}{AF^2}.\frac{AF}{AB}=\frac{AC}{AB}.\frac{AE}{AF}=1\)
Theo định lí Menelaus thì 3 điểm G,I,M thẳng hàng
Dễ thấy AIHG là hình bình hành => IG chia đôi AH. Hay MI chia đôi AH. Vậy T là trung điểm AH.