Thông báo: Cuộc thi học cùng Olm mỗi ngày học giỏi học hay năm 2024. (Điểm danh những bạn học sinh giỏi tại đây! 30 gp cho những bạn HSG đăng kí). Quà tặng GP và nhiều giải thưởng cho các em sẽ xuất hiện.
Cô Thương Hoài thân ái chào toàn thể các thành viên của Olm. Hôm nay là ngày thật đặc biệt với thiếu nhi toàn thế giới và chắc chắn cũng sẽ là ngày đầy tuyệt vời với các bạn trên Olm. Bởi vì hôm nay sẽ có rất nhiều sự kiện hot trên diễn đàn, mưa gp sẽ là cơn gió lành thổi tan cái nắng oi ả và vất vả của những ngày thi. Cụ thể thế nào thì mời các em xem chú ý theo dõi các sự kiện dưới đây:
1; Sự kiện thứ nhất: Tri ân gp quà mùng một tháng sáu cho các học viên của olm đạt thành tích cao trong học tập
Bước 1:
Bình luận thứ nhất: Em đăng kí tham gia sự kiện: "Học cùng Olm mỗi ngày học giỏi học hay.
Bình luận thứ hai: Giới thiệu về bản thân và những thành tích đã đạt được trong năm qua.
Bước 2: nếu muốn nhận thêm giải bằng hiện vật các em tham gia bình chọn học viên được yêu thích nhất qua face book của ban tổ chức
Các em gửi giấy khen, giấy chứng nhận, ảnh bản thân nếu đã từng thưởng các hiện vật của Olm thì ảnh chụp bản thân kèm hiện vật vào zalo của ban tổ chức số 0385 168 017 kèm theo link cá nhân trên olm. kèn số điện thoại liên lạc.
Bước 3. Ban tổ chức sẽ gửi mã số bình chọn, link bình chọn cho các em. giải nhất trị giá 100 000 đồng và nhiều giải khác.
Thời hạn tham gia từ hôm nay đến hết ngày 30 tháng 8 năm 2024.
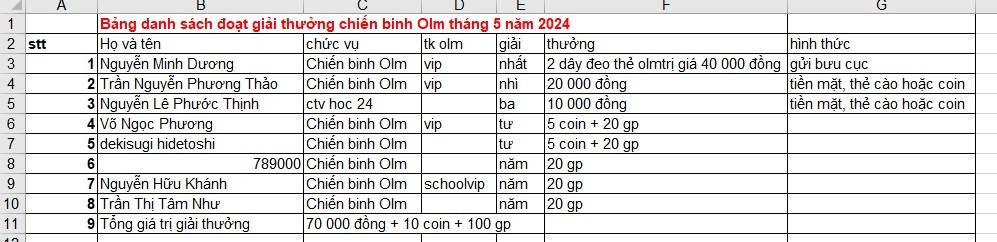
2; Sự kiện thứ hai: Danh sách chiến binh được thưởng câu lạc bộ chiến binh olm (xem bình luận)
Để nhận thưởng chiến binh olm các em bình luận:
Bình luận thứ nhất: Em đăng kí nhận thưởng câu lạc bộ chiến binh Olm
Bình luận thứ hai em đăng kí nhận bằng:.... (tiền mặt, thẻ cào, gp)
Chọn hình thức thích hợp điền vào chỗ..
Thời hạn nhận thưởng từ khi có thông báo tới hết ngày 30 tháng 6 năm 2024.3;
3; Sự kiện thứ ba: Danh Sách thí sinh đạt giải bài học cuộc sống:
| stt |
Họ Và Tên |
link |
giải |
thưởng |
| 1 |
Lương Lê Bích Trâm |
https://olm.vn/thanhvien/a_luonglebichtram |
nhì |
một móc khóa olm trị giá 25 000 đồng
Và một dây đeo thẻ olm trị gía 20 000 đồng
|
| 2 |
Trần Thị Tâm Như |
https://olm.vn/thanhvien/nhuc3112345 |
ba |
thẻ cào 10 000 đồng |
Để nhận thưởng các em thực hiện các yêu cầu sau:
Bình luận thứ nhất: Em đăng kí nhận thưởng cuộc thi bài học cuộc sống.
Bình luận thứ hai em đăng kí nhận bằng:.... (tiền mặt, thẻ cào, gp, hiện vật)
Chọn hình thức thích hợp điền vào chỗ...
Thời hạn nhận thưởng từ khi có thông báo tới hết ngày 30 tháng 6 năm 2024
Một lần nữa chúc các em ngày quốc tế thiếu nhi nhiều niềm vui và an yên bên gia đình.

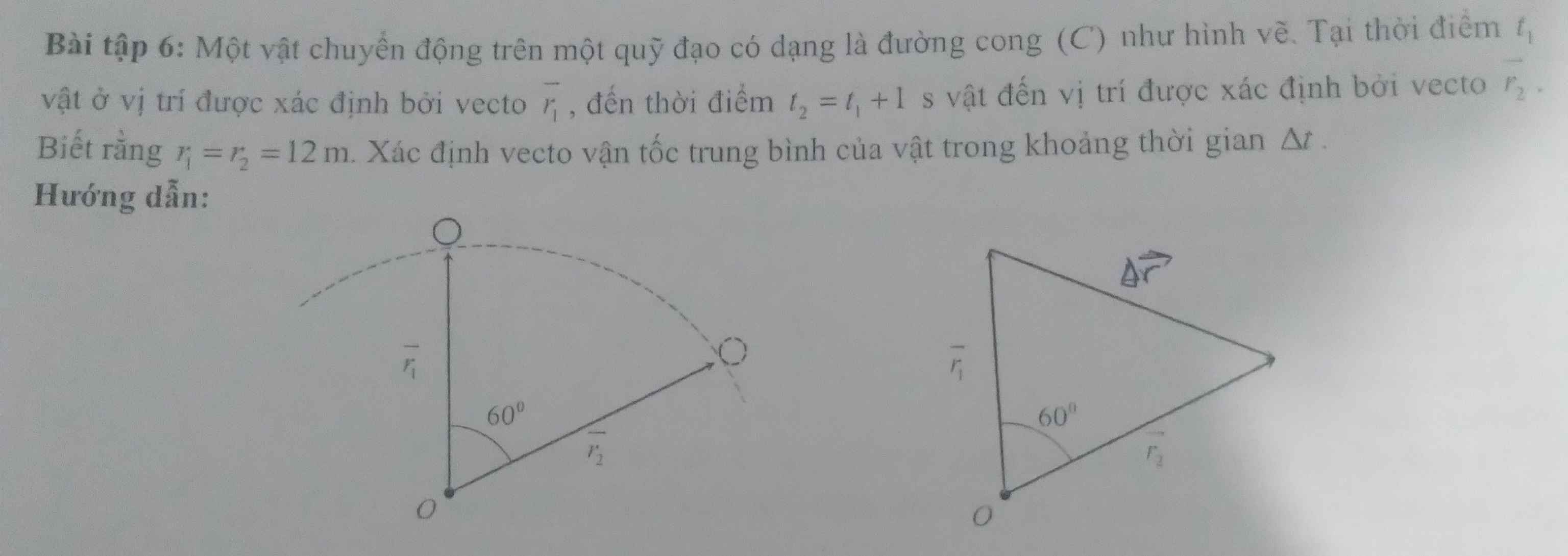


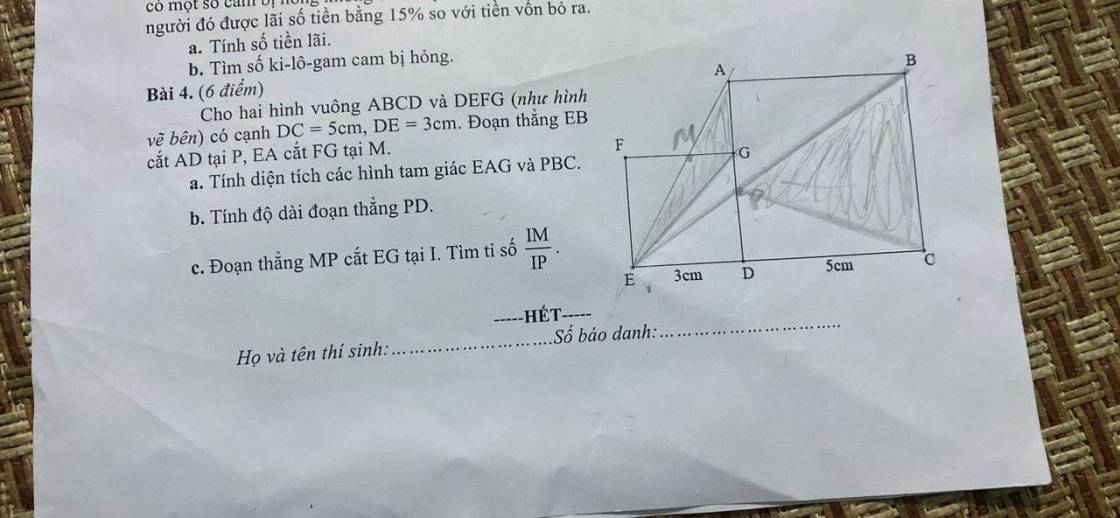
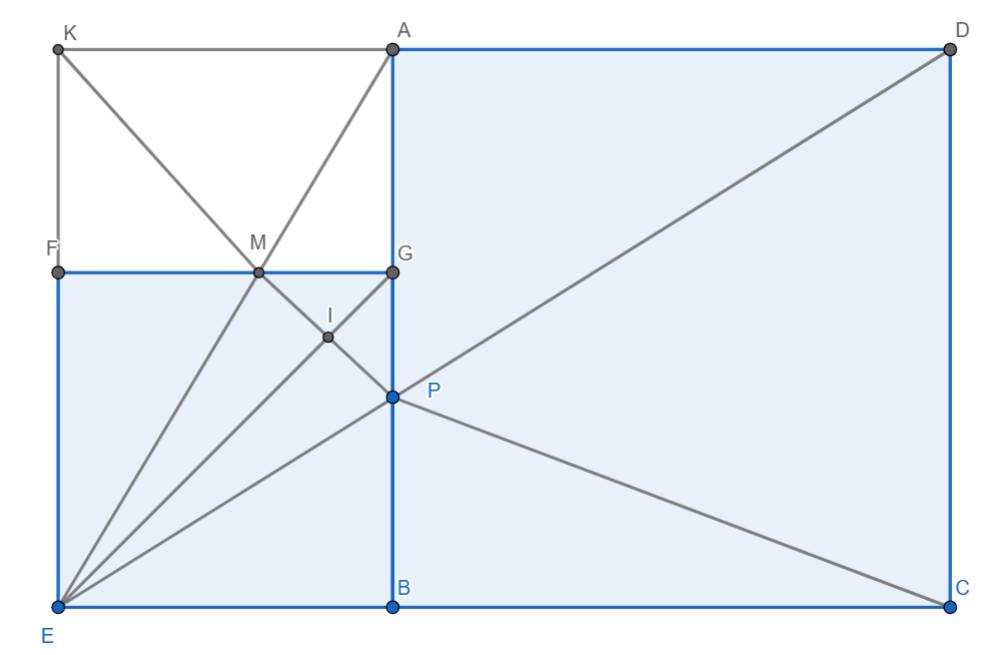











khó quá
Khó thì để cho người khác còn làm !