TỔNG KẾT HOẠT ĐỘNG ĐIỀN KHẢO SÁT VỀ GIÁO DỤC TRỰC TUYẾN TRÊN OLM VÀ HOC24
Link điền khảo sát: https://olm.vn/s/khaosatOLMHoc24
Link bài viết chi tiết về thể lệ: https://olm.vn/s/khaosatOLMthele

Trải qua hơn ba tuần thu thập dữ liệu điền khảo sát, nhóm nghiên cứu đã nhận được hơn 10.000 đơn điền khảo sát đến từ cộng đồng OLM và Hoc24. Thay mặt cho nhóm nghiên cứu khoa học OLM, chúng tôi xin cảm ơn sự đóng góp to lớn đến từ tất cả các bạn. Nhờ có các bạn, OLM và Hoc24 sẽ tiếp tục cải thiện dịch vụ và hướng đến sự thỏa mãn tối đa đối với tất cả người dùng trên các trang.
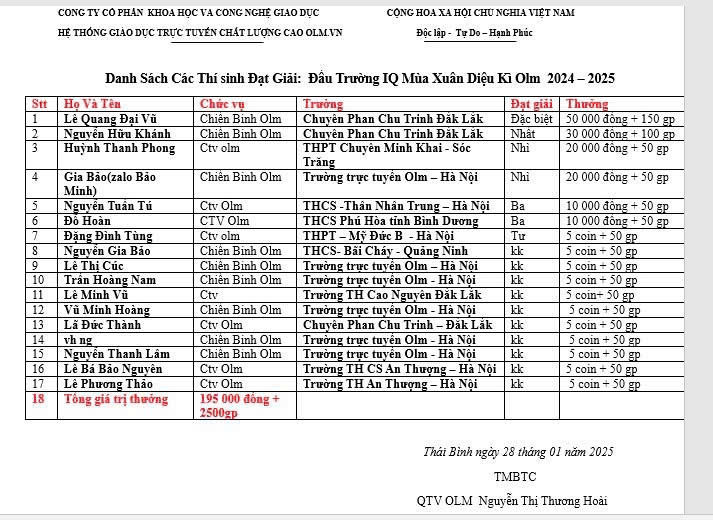
Ban tổ chức xin được công bố giải thưởng của hoạt động lần này là như sau:
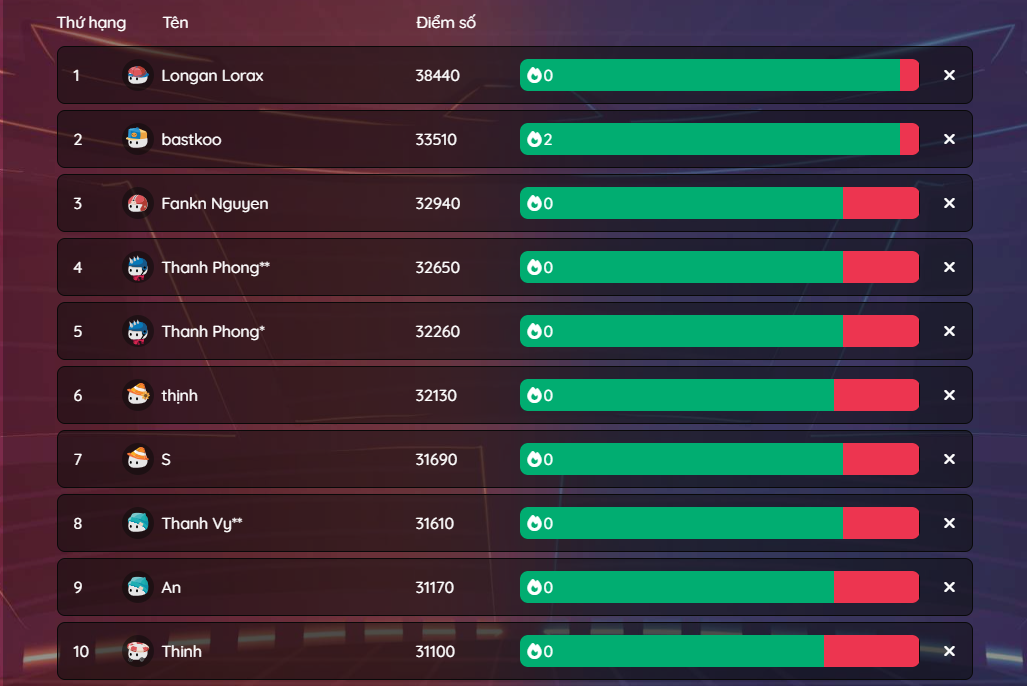
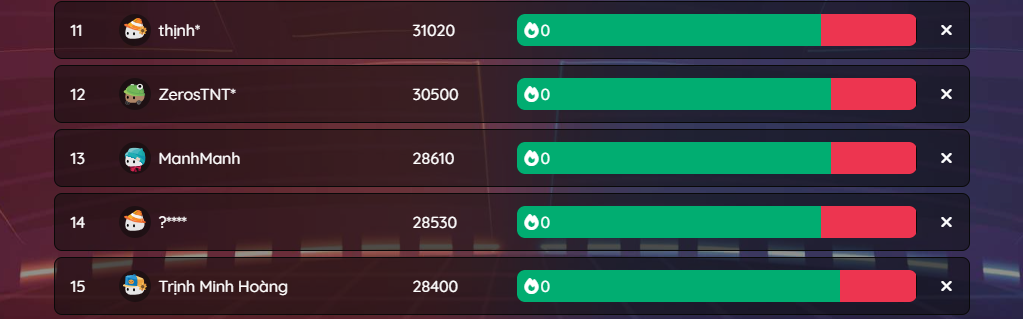
Đối với mục c) 10 người mời được nhiều bạn điền form nhất sẽ được nhận phần thưởng tiền mặt đến từ nhà tài trợ OLM và Hoc24, xin chúc mừng các bạn:
1 GIẢI NHẤT: 600.000đ. Nguyễn Lê Phước Thịnh - 3.196 lượt mời.
1 GIẢI NHÌ: 300.000đ. vh ng - 3.195 lượt mời.
1 GIẢI BA: 150.000đ. Trần Huy Trí Dũng - 3.156 lượt mời.
2 GIẢI TƯ: 100.000đ.
Đỗ Công Huy - 1.021 lượt mời.
Lê Bá Bảo Nguyên - 348 lượt mời.
5 GIẢI NĂM: 50.000đ.
Tui hổng có tên =33 - 164 lượt mời.
Nguyễn Khắc Toàn - 98 lượt mời.
Lê Phương Thảo - 77 lượt mời.
Hbth - 49 lượt mời.
Trần Thanh Tùng - 27 lượt mời.
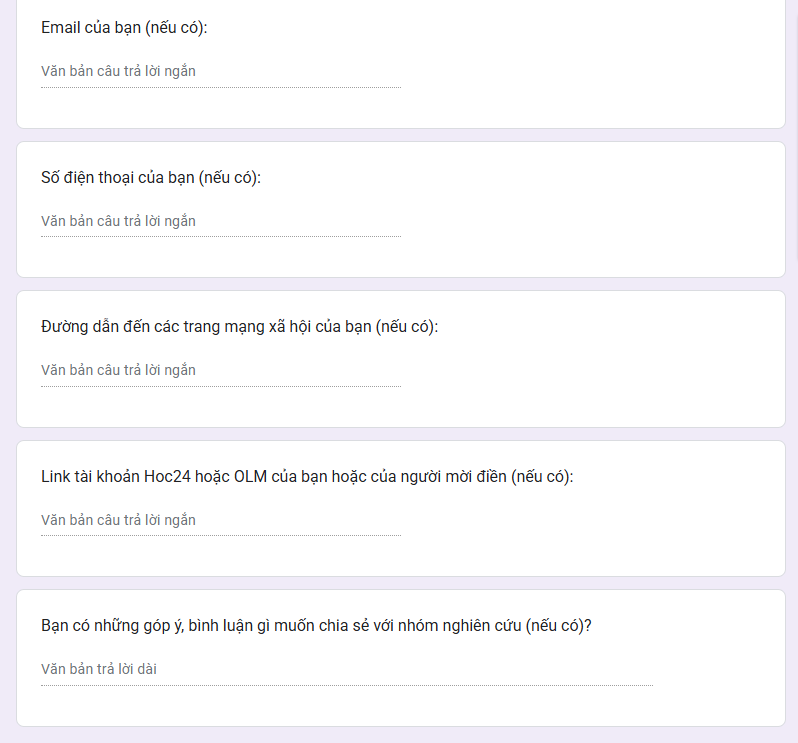
Để nhận thưởng, các bạn hãy gửi tin nhắn riêng đến thầy với những thông tin sau nhé:
- Họ và tên.
- Lớp, trường đang theo học.
- Giải thưởng đạt được và giá trị giải.
- Số tài khoản ngân hàng, tên chủ sở hữu số tài khoản, tên ngân hàng (hoặc số tài khoản Momo, đổi sang thẻ cào, đổi sang COIN, nếu các bạn muốn).
- Số điện thoại hoặc email liên hệ.
Đối với mục b) 1 vé tham gia bốc thăm trúng thưởng trong chương trình Livestream diễn ra dự kiến vào giữa tháng 4/2025, BTC sẽ có một buổi livestream dự kiến diễn ra vào giữa tháng 4, những thông tin mới nhất về sự kiện các bạn có thể cập nhật trên diễn đàn OLM và Hoc24 nhé.
Đối với mục d) 50 người mời được nhiều bạn điền form nhất (tối thiểu 5 bạn) sẽ được nhận giấy chứng nhận có dấu đỏ đến từ Công ty cổ phần Công nghệ Giáo dục Việt Nam, nếu các bạn đã mời được ít nhất 5 người, hãy nhắn tin riêng cho thầy những thông tin sau để nhận giấy chứng nhận nhé:
- Họ và tên.
- Lớp, trường đang theo học.
- Số người đã mời.
Xin chúc mừng các bạn đã đạt giải! BTC rất mong sẽ được thấy sự tham gia của các bạn trong những sự kiện sắp tới do OLM và Hoc24 tổ chức!
Với form khảo sát ở trên, BTC vẫn mở form điền để tiếp nhận những đóng góp của các bạn. Nếu các bạn muốn đóng góp và đánh giá chất lượng những nền tảng học tập trực tuyến, hãy truy cập link form BTC đã gửi ở đầu bài viết và đánh giá nhé!
Trân trọng,
Đội ngũ nghiên cứu OLM.







chúc mừng nha
Nhận thưởng gì vậy ạ