(2 điểm)
a. Hiện tượng cảm ứng điện từ là hiện tượng gì? Nêu điều kiện xuất hiện dòng điện cảm ứng.
b. Nêu cấu tạo và nguyên tắc hoạt động của máy phát điện xoay chiều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Muốn dựng ảnh A'B' của AB qua thấu kính (AB vuông góc với trục chính của thấu kính, A nằm trên trục chính), chỉ cần dựng ảnh B' của B bằng cách vẽ đường truyền của hai trong ba tia sáng đặc biệt, sau đó từ B' hạ vuông góc xuống trục chính ta có ảnh A' của A.
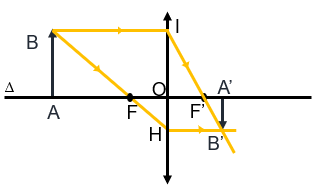
Ảnh thu được là ảnh thật, ngược chiều vật.
b. h=2cm;d=36cm;f=12cmh=2cm;d=36cm;f=12cm
Xét \Delta ABFΔABF đồng dạng với \Delta OHFΔOHF, ta có: \dfrac{AB}{OH}=\dfrac{AF}{OF}OHAB=OFAF
Vì OH=A'B'OH=A′B′ \Rightarrow\dfrac{AB}{A'B'}=\dfrac{AF}{OF}\Rightarrow\dfrac{h}{h'}=\dfrac{d-f}{f}⇒A′B′AB=OFAF⇒h′h=fd−f
\Rightarrow h'=\dfrac{hf}{d-f}=\dfrac{2.12}{36-12}=1cm⇒h′=d−fhf=

a. ARN được tổng hợp theo 2 nguyên tắc là nguyên tắc bổ sung và nguyên tắc khuôn mẫu, ARN là bản sao của một đoạn ADN (tương ứng với một gen), ngoài ra ở một số virut ARN là vật chất di truyền.
Nôi dung nguyên tắc bổ sung: Trong di truyền học, sinh học phân tử, nguyên tắc bổ sung là nguyên tắc liên kết giữa một nucleotide và một nucleotide khác đối diện, trong các đại phân tử DNA hay RNA.
Nội dung nguyên tắc khuôn mẫu: các mạch ADN của mẹ làm mạch khuôn để tổng hợp mạch ADN mới (có ở nhân đôi ADN)

a) Điện trở tương đương của mạch là:
Rtđ=R1+R2=25+15=40 (Ω)
Cường độ dòng điện đi qua mỗi điện trở là:
I1=I2=I=U/Rtđ=12/40=0,3 (A)
b) Điện trở của R2 là:
R2=\(\dfrac{\rho\times l}{S}\)=15 (Ω)
<=> \(\dfrac{0,5\times10^{-6}\times l}{0,06\times10^{-6}}\)=15
<=>0,5.l=0,9
<=>l=1,8 (m)
c) Hiệu điện thế hai đầu R2 là :
U2=U-Uđ=12-6=6 (V)
Cường độ dòng điện đi qua R1 là:
I1=\(\dfrac{U_đ}{R_1}=\dfrac{6}{25}=0,24\) (A)
Cường độ dòng điện đi qua đèn là:
Iđ=\(\dfrac{P_đ}{U_đ}=\dfrac{3}{6}=0,5\) (A)
Cường độ dòng điện đi qua R2 là:
I2=I=Iđ+I1=0,5+0,24=0,74 (A)
Điện trở của R2 lúc đó là:
R2=U2/I2=6/0,74≈8,11 (Ω)
a)\(R_1ntR_2\Rightarrow\)\(R_tđ=R_1+R_2=25+15=40\)\(\Omega\)
\(I_1=I_2=I=\dfrac{U}{R_{tđ}}=\dfrac{12}{40}=0,3A\)
b)Điện trở dây: \(R=\rho\cdot\dfrac{l}{S}\)
\(\Rightarrow\)Chiều dài dây: \(l=\dfrac{R\cdot S}{\rho}=\dfrac{15\cdot0,06\cdot10^{-6}}{0,5\cdot10^{-6}}=1,8m\)
c)\(R_Đ=\dfrac{U^2_Đ}{P_Đ}=\dfrac{6^2}{3}=12\Omega;I_{Đđm}=\dfrac{P_Đ}{U_Đ}=\dfrac{3}{6}=0,5A\)
CTM: \(\left(R_1//Đ\right)ntR_2\)
Để đèn sáng bình thường\(\Rightarrow I_Đ=I_{Đđm}=0,5A\Rightarrow U_Đ=0,5\cdot12=6V\Rightarrow U_{1Đ}=6V\)
\(U_1=6V\Rightarrow I_1=\dfrac{6}{25}=0,24A\)
\(I_2=I_1+I_Đ=0,24+0,5=0,74A\)
\(U_2=U-U_{1Đ}=12-6=6V\)
\(R_2=\dfrac{U_2}{I_2}=\dfrac{6}{0,74}=\dfrac{300}{37}\approx8,108\Omega\)

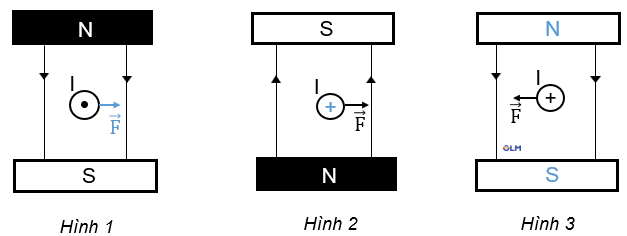
a. Quy tắc bàn tay trái: Đặt bàn tay trái sao cho các đường sức từ hướng vào lòng bàn tay, chiều từ cổ tay đến ngón tay giữa hướng theo chiều dòng điện thì ngón tay cái choãi ra 90° chỉ chiều của lực điện từ.
a. Quy tắc xác định chiều của lực điện từ (Quy tắc bàn tay trái): Đặt bàn tay trái sao cho các đường sức từ hướng vào lòng bàn tay, chiều từ cổ tay đến ngón tay giữa hướng theo chiều dòng điện thì ngón tay cái choãi ra 90o chỉ chiều của lực điện từ.
b. Hình 1 cần xác định chiều lực từ tác dụng lên dây dẫn.

a) Công suất tỏa nhiệt của bếp là:
\(P=I^2.R=2,5^2.80=500\left(W\right)\)
b) Nhiệt lương để đun nước từ 25oC
\(Q_i=m.c.\Delta t=1,5.4200.\left(100-25\right)=472500\left(J\right)\)
Nhiệt lượng bếp tỏa ra là:
\(Q=I^2.R.t=P.t=500.20.60=600000\left(J\right)\)
Hiệu suất của bếp là:
\(H=\dfrac{Q_i}{Q}.100\%=\dfrac{472500}{600000}.100\%=78,75\%\)
a, Nhiệt lượng mà bếp tỏa ra trong là: Q=I2Rt=2,52.80.=500J
b, nước sôi ở 100oC, m = 1,5 kg. Nhiệt lượng mà nước nhận được là: Qn = m.c.(t2 - t1) = 1,5 . 4200 . (100 - 25) = 472500 J
Nhiệt lượng mà bếp điện tỏa ra trong 20 phút là: Qtp = 500 . 20 .60 = 600000 J
Hiệu suất của bếp là: H = Aci/Atp . 100% = 472500/600000 . 100%= 78,75%
c, Điện năng bếp điện tiêu thụ trong 30 ngày là: A=I2Rt=2,52.80.3.30=45000(W.h)=45(kW.h)
Tiền điện phải trả là: 45 . 1500 = 67500 (đồng) em không biết cách viết a trên b như thế nào nên em viết :/

a. Quy tắc bàn tay trái (còn gọi là quy tắc Fleming) là quy tắc định hướng của lực. Do một từ trường tác động lên một đoạn mạch có dòng điện chạy qua và đặt trong từ trường. Đặt bàn tay trái sao cho các đường cảm ứng từ hướng vào lòng bàn tay. Chiều từ cổ tay đến ngón tay giữa hướng theo chiều dòng điện. Thì ngón tay cái choãi ra 90° chỉ chiều của lực điện từ.
b. Kim nam châm về phía của cuộn dây,khi đóng khóa K dòng điện sẽ chạy rồi áp dụng quy tắc nắm bàn tay phải thì một bên là cực nam, một bên là cực bắc nên chúng sẽ hút nhau.
a) Nắm bàn tay phải, rồi đặt sao cho bốn ngón tay hướng theo chiều dòng điện chạy qua các vòng dây thì ngón tay cái choãi ra chỉ chiều của đường sức từ trong lòng ống dây.
b) Kim nam châm bị đẩy ra, vì khi đóng khóa K thì dòng điện sẽ chạy rồi áp dụng quy tắc nắm tay phải thì 2 bên là ống dây cực bắc mà bên kim nam châm cũng cực bắc suy ra 2 bên đẩy nhau

Bạn nhân chéo rồi rút gọn thì được:
\(x^4-3x^3+3x+1=0\\ \Leftrightarrow(x^2-2x-1)(x^2-x-1)=0\)
Bạn tự giải tiếp nhé.

Ta có thể dùng cosy hoặc đặt a,b lần lượt là hai số hạng vế trái của phương, đưa phương trình về hệ phương trình không triệt để. Từ đó giải phương.
Đầu kiện: \(x\ge0\)
Ta có:
\(4\sqrt{x}=2\sqrt{4x}\le4+x\\ \Rightarrow x^2+4-4\sqrt{x}\ge x^2-x\\ \Rightarrow\sqrt{x^2+4-4\sqrt{x}}\ge\sqrt{x^2-x}\)
\(6\sqrt{x}=2\sqrt{9x}\le9+x\\ \Rightarrow\sqrt{x^2+4-6\sqrt{x}}\ge\sqrt{x^2-x-5}\)
Suy ra \(1\ge\sqrt{x^2-x}+\sqrt{x^2-x-5}\)
Đặt \(\sqrt{x^2-x}=a;0\le a\le1\\ \sqrt{x^2-x-5}=b;0\le b\le1.\\ \Rightarrow a^2-b^2=\left(x^2-x\right)-\left(x^2-x-5\right)=5.Vôlí\)
Vậy phương trình đã cho vô nghiệm.

Với `x \ne 0,x \ne 1` có:
`A=([x\sqrt{x}]/[\sqrt{x}-1]-[x^2]/[x\sqrt{x}])(1/\sqrt{x}-1)^2`
`A=([x\sqrt{x}]/[\sqrt{x}-1]-x/\sqrt{x})([1-\sqrt{x}]/\sqrt{x})^2`
`A=[x^2-x(\sqrt{x}-1)]/[\sqrt{x}(\sqrt{x}-1)].[(\sqrt{x}-1)^2]/x`
`A=[x(x-\sqrt{x}-1)]/\sqrt{x}.[\sqrt{x}-1]/x`
`A=[x-\sqrt{x}-1]/[\sqrt{x}-1]`
Hello