ĐIỀN KHẢO SÁT VỀ GIÁO DỤC TRỰC TUYẾN, NHẬN NGAY 5 COIN, 10GP CÙNG HÀNG TRĂM GIẢI THƯỞNG LÊN ĐẾN HÀNG CHỤC TRIỆU ĐỒNG
Link điền khảo sát: https://bit.ly/khaosathoc24olm

Một trong những hoạt động chính trong chuỗi sự kiện, chính là để giúp những người xây dựng nền tảng, nội dung và dịch vụ như chúng tôi - các thầy cô các hệ thống học tập trực tuyến có thể hỗ trợ cộng đồng các bạn học sinh và giúp các bạn có một trải nghiệm tốt hơn. Khảo sát được thực hiện bởi các thầy cô trong hội đồng điều hành, ban quản lí các nền tảng học tập trực tuyến OLM và Hoc24, nên chúng tôi cam kết uy tín tuyệt đối.
Các bạn sẽ trả lời tổng cộng 18 câu hỏi đánh giá trên thang đo từ 1 đến 5, đánh giá trên mọi lĩnh vực của tất cả các nền tảng học tập trực tuyến nói chung. Chúng tôi sẽ sử dụng những kết quả đó và xin cam kết sẽ cải thiện triệt để, hoàn toàn những vấn đề còn tồn đọng để cung cấp đến cho các bạn những sản phẩm, dịch vụ tốt nhất. Thời gian hoàn thiện khảo sát dự kiến là từ 5 đến 10 phút. Chúng tôi cam kết thông tin bạn cung cấp sẽ được bảo mật tuyệt đối.
Về cơ cấu phần thưởng trong hoạt động này:
Lưu ý phần thưởng sẽ được chuyển đến muộn nhất trong 7 ngày.
1. Phần thưởng cá nhân: mỗi form điền thành công sẽ nhận được trực tiếp 5 COIN và 10GP vào tài khoản OLM hoặc Hoc24. Ngoài ra, các bạn sẽ nhận được trong hộp thư tài khoản một mã giảm giá 10% tất cả các dịch vụ của OLM, gói 1 tháng đến 1 năm.
Nếu các bạn mời được người bạn khác điền form (người bạn đó có nhập thông tin của bạn vào form họ điền trong mục nhận thưởng), bạn sẽ nhận được trực tiếp 2 COIN và 3GP vào tài khoản OLM hoặc Hoc24. Tối đa 5 lần nhận phần thưởng này.
2. Phần thưởng quỹ: mỗi form điền thành công sẽ nhận được:
a) 1 vé tham gia bốc thăm trúng thưởng trong chương trình Livestream diễn ra dự kiến vào giữa tháng 4/2025.
Cơ cấu giải thưởng:
1 GIẢI NHẤT: 800.000đ.
1 GIẢI NHÌ: 400.000đ.
2 GIẢI BA: 200.000đ.
4 GIẢI TƯ: 100.000đ.
10 GIẢI NĂM: 40.000đ.
20 GIẢI KHUYẾN KHÍCH: 20.000đ.
b) 10 người mời được nhiều bạn điền form nhất sẽ được nhận phần thưởng tiền mặt đến từ nhà tài trợ OLM và Hoc24.
Cụ thể phần thưởng:
1 GIẢI NHẤT: 800.000đ.
1 GIẢI NHÌ: 400.000đ.
1 GIẢI BA: 200.000đ.
2 GIẢI TƯ: 100.000đ.
5 GIẢI NĂM: 50.000đ.
c) 50 người mời được nhiều bạn điền form nhất (tối thiểu 5 bạn) sẽ được nhận giấy chứng nhận có dấu đỏ đến từ Công ty cổ phần Công nghệ Giáo dục Việt Nam. Chúng tôi cam kết giấy chứng nhận sẽ được cung cấp đầy đủ dữ liệu, và các bạn có thể sử dụng với hồ sơ của các bạn ở bất cứ hoạt động nào các bạn muốn, và công ty sẽ chứng thực nếu cần xác minh.
Thời gian chúng tôi thực hiện thu thập dữ liệu từ khảo sát là từ hôm nay (7/2/2025) đến hết ngày 28/2/2025.
Form khảo sát được xây dựng và chịu trách nhiệm bởi:
1. Hà Đức Thọ - Cố vấn nghiên cứu, quản lí cấp cao OLM và Hoc24.
2. Lê Quốc Trần Anh - Trưởng nhóm nghiên cứu, giáo viên tại OLM và Hoc24.
3. Hà Quang Minh - Phó trưởng nhóm nghiên cứu, giáo viên tại OLM và Hoc24.
Cùng với rất nhiều thầy cô khác tại các viện nghiên cứu...
Chúng tôi rất hi vọng các bạn sẽ đóng góp thật thẳng những suy nghĩ và đánh giá của mình, để chúng tôi cải thiện các nền tảng học tập trực tuyến trong Việt Nam nói chung một cách tốt nhất, trọng tâm nhất. Xin cảm ơn!
Một số câu hỏi thường gặp:
1. Tôi điền thông tin nhận thưởng ở đâu?
Trả lời: Trong phần cuối cùng của khảo sát, đây là mục điền thông tin nhận thưởng. Để nhận thưởng COIN và GP, các bạn bắt buộc cần điền vào mục tài khoản OLM hoặc Hoc24 (câu hỏi thứ tư). Nếu không nhận COIN và GP, các bạn bắt buộc cần điền vào mục email của bạn để chúng tôi gửi thưởng qua email. Những câu hỏi còn lại đều không bắt buộc phải điền.
2. Nếu tôi mời được bạn và tôi muốn nhận thưởng, bạn tôi cần điền form trong mục nhận thưởng như thế nào?
Trả lời: Người bạn mà bạn mời sẽ điền nhận thưởng cho bạn trong phần cuối cùng. Nếu bạn muốn nhận COIN và GP, bạn của bạn bắt buộc phải điền link tài khoản OLM hoặc Hoc24 của chính bạn, xong chúng tôi sẽ chuyển thưởng cho bạn.
Nếu bạn không muốn nhận COIN và GP (chỉ muốn nhận mã giảm giá hoặc tham gia lấy các giải thưởng quỹ), người bạn của bạn bắt buộc phải điền email của chính bạn, để chúng tôi thống kê. Bảng xếp hạng sẽ được cập nhật 3 ngày một lần để các bạn theo dõi tiến độ.
3. Tôi có bị giới hạn số lần mời bạn không?
Trả lời: Bạn không bị giới hạn số lần mời, và không có giới hạn số quyền lợi thưởng được nhận.
4. Nếu tôi hoặc bạn tôi điền nhầm thông tin nhận thưởng, tôi phải làm gì? Trả lời: Trong trường hợp đó, chúng tôi rất tiếc nhưng chúng tôi không thể hỗ trợ sâu vấn đề này. Tuy nhiên, bạn có thể thử liên hệ chúng tôi chính qua những bài viết thông báo chúng tôi đăng và chúng tôi sẽ cố gắng hỗ trợ hết sức.


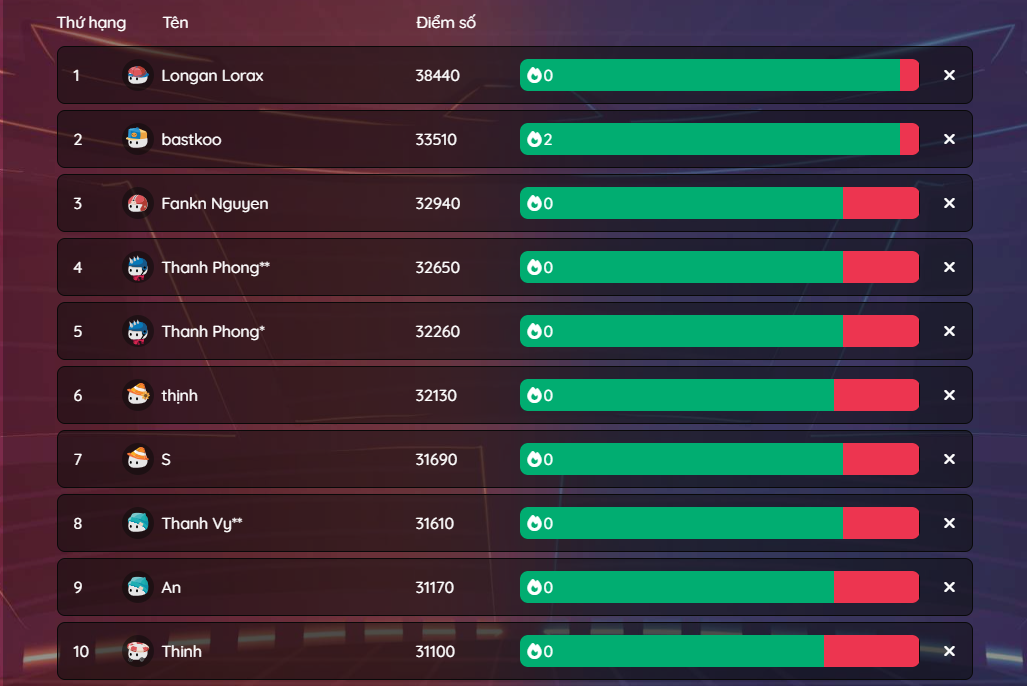
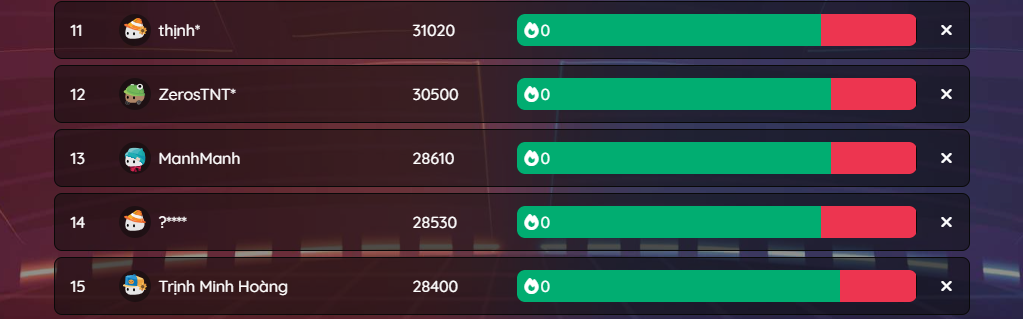







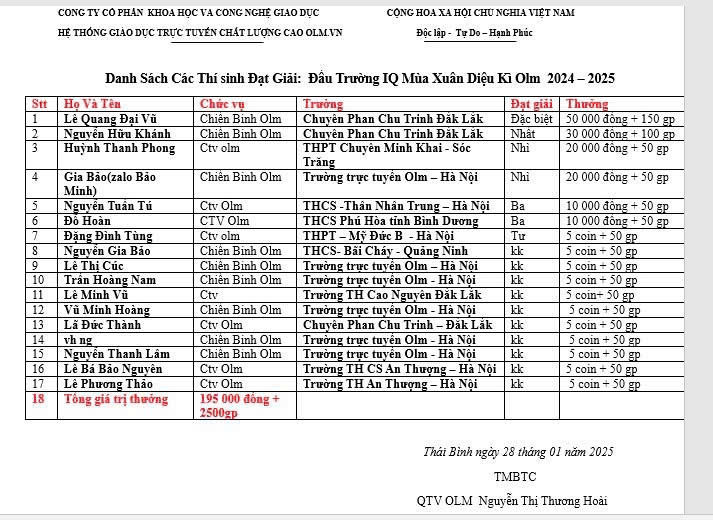
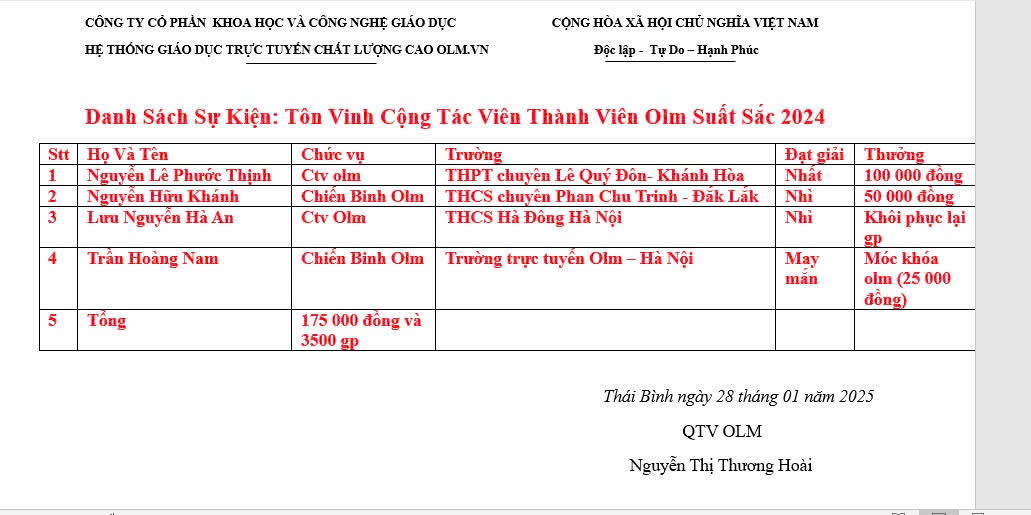
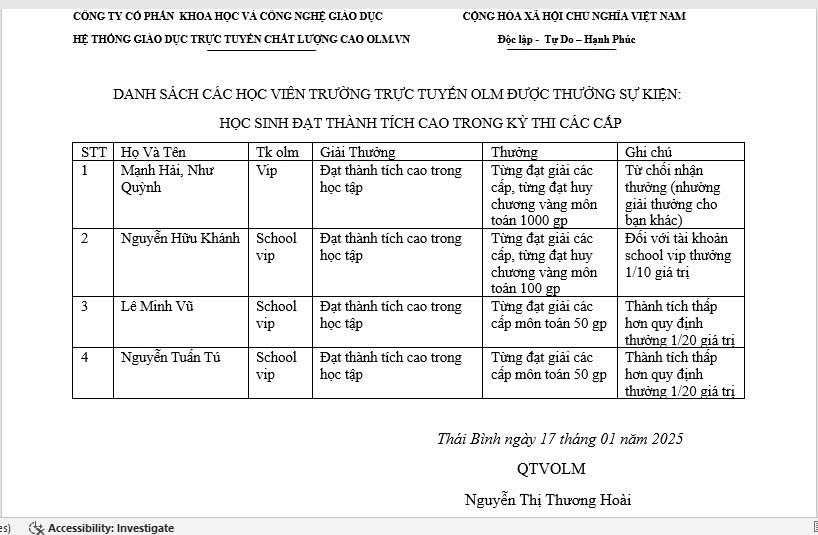
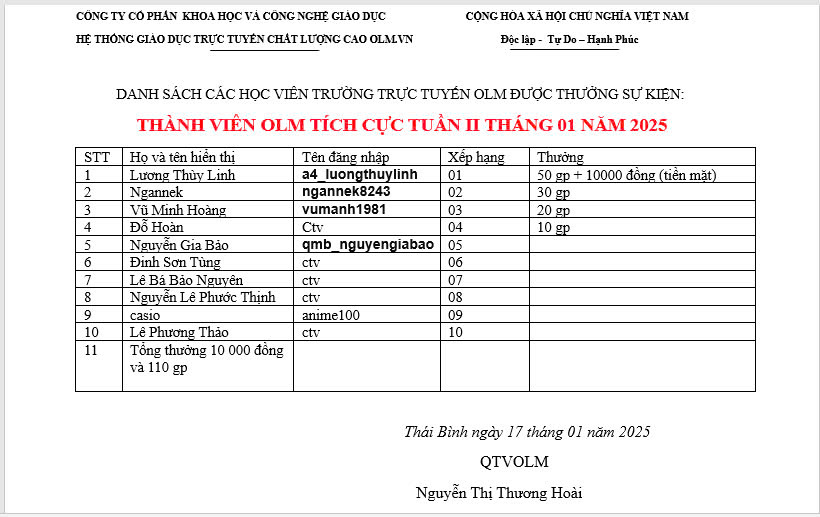
Tham gia ngay đi mn ơi!
Giải thưởng hấp dẫn lắm!