Tính giá trị biểu thức \(P=\frac{\sqrt{xy}+\sqrt{y^2}}{y}-\sqrt{\frac{x}{y}}\)với x,y thỏa mãn đẳng thức: \(4x^2+9y^2=16xy\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+) Xét n≥27n≥27
Ta có : A=427+42016+4n=427⋅(1+41989+4n−27)A=427+42016+4n=427⋅(1+41989+4n−27)
Dễ thấy 427=22⋅27=(227)2427=22⋅27=(227)2 là số chính phương
Do đó để A là số chính phương thì 1+41989+4n−271+41989+4n−27 là số chính phương
Đặt B2=1+41989+4n−27B2=1+41989+4n−27 và n−27=kn−27=k
Khi đó : B2=1+41989+4kB2=1+41989+4k
⇔B2−(2k)2=1+41989⇔B2−(2k)2=1+41989
⇔(B−2k)(B+2k)=1+41989⇔(B−2k)(B+2k)=1+41989
Ta có : B+2k≤1+41989B+2k≤1+41989 và B−2k≥1B−2k≥1
⇒B−2k+41989≥1+41989≥B+2k⇒B−2k+41989≥1+41989≥B+2k
Hay B−2k+41989≥B+2kB−2k+41989≥B+2k
⇔2⋅2k≤41989⇔2⋅2k≤41989
⇔2k+1≤23978⇔2k+1≤23978
⇔k+1≤3978⇔k+1≤3978
⇔k≤3977⇔k≤3977
Để n lớn nhất thì k lớn nhất,nên:
Nếu k=3977k=3977 ta có B2=1+41989+43977B2=1+41989+43977
⇔B2=(23977)2+2⋅23977+1⇔B2=(23977)2+2⋅23977+1
⇔B2=(23977+1)2⇔B2=(23977+1)2( đúng )
Vậy k=3977⇒n=3977+27=4004k=3977⇒n=3977+27=4004( thỏa )
+) Xét n≤27n≤27 nên hiển nhiên n≤4004n≤4004
Suy ra n lớn nhất để A là số chính phương thì n=4004
Nếu thấy đúng thì k cho mình nha
\(A=4^{27}+4^{2016}+4^n\)
Với \(n\ge27\):
\(A=4^{27}\left(1+4^{1989}+4^{n-27}\right)\)
\(A\)là số chính phương suy ra \(B=4^{n-27}+4^{1989}+1\)là số chính phương.
\(B=\left(2^{n-27}\right)^2+2^{3978}+1\)
\(=\left(2^{3977+n-4004}\right)^2+2.2^{3977}+1\)
Với \(n=4004\)thì:
\(B=\left(2^{3977}\right)^2+2.2^{3977}+1=\left(2^{3977}+1\right)^2\)là số chính phương.
Với \(n>4004\)thì:
\(B>\left(2^{3977+n-4004}\right)^2\)
\(B< \left(2^{3977+n-4004}\right)^2+2.2^{3977+n-4004}+1\)
\(=\left(2^{3977+n-4004}+1\right)^2\)
Suy ra \(\left(2^{3977+n-4004}\right)^2< B< \left(2^{3977+n-4004}+1\right)^2\)do đó \(B\)không là số chính phương.
Vậy giá trị lớn nhất của \(n\)là \(4004\).

\(n^2+2n+\sqrt{n^2+2n+18}+9\)là số chính phương thì \(\sqrt{n^2+2n+18}\)là số tự nhiên.
Khi đó \(n^2+2n+18=m^2\)
\(\Leftrightarrow\left(m-n-1\right)\left(m+n+1\right)=1.17\)
Do \(m,n\)là số tự nhiên nên
\(\hept{\begin{cases}m-n-1=1\\m+n+1=17\end{cases}}\Leftrightarrow\hept{\begin{cases}m=9\\n=7\end{cases}}\)
Với \(n=7\)thì \(n^2+2n+\sqrt{n^2+2n+18}+9=7^2+2.7+\sqrt{7^2+2.7+18}+9\)
\(=81=9^2\)là số chính phương (thỏa mãn).
Vậy \(n=7\).

\(2\ge2x+3y\ge2\sqrt{2x.3y}\Rightarrow xy\le\frac{1}{6}.\)
\(A=\frac{4}{4x^2+9y^2}+\frac{9}{xy}=\frac{4}{4x^2+9y^2}+\frac{4}{12xy}+\frac{26}{3xy}\ge\frac{\left(2+2\right)^2}{4x^2+9y^2+12xy}+\frac{26}{3xy}\)
\(\ge\frac{4^2}{2^2}+\frac{26}{3.\frac{1}{6}}=56\)
Dấu \(=\)khi \(\hept{\begin{cases}\frac{2}{4x^2+9y^2}=\frac{2}{12xy}\\2x=3y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{1}{3}\end{cases}}\)
Áp dụng bất đẳng thức Cô – si cho hai số dương, ta có: 2x + 3y ≥ 2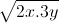
⇔ 2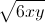 ≤ 2x + 3y
≤ 2x + 3y
Mà 2x + 3y ≤ 2
Do đó 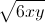 ≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
A = 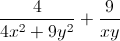 = 4(
= 4(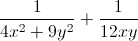 ) +
) + 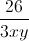 ≥ 4
≥ 4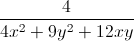 +
+ 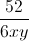 = 16
= 16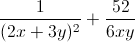 ≥ 16.
≥ 16.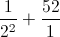 = 56
= 56
Dấu “ = “ xảy ra ⇔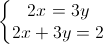 ⇔
⇔ 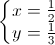
Vậy giá trị nhỏ nhất của biểu thức A là 56.

sửa đề : \(\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)
\(=\sqrt{5^2+2.5\sqrt{2}+2}-\sqrt{4^2+2.4\sqrt{2}+2}\)
\(=\sqrt{\left(5+\sqrt{2}\right)^2}-\sqrt{\left(4+\sqrt{2}\right)^2}=\left|5+\sqrt{2}\right|-\left|4+\sqrt{2}\right|\)
\(=5+\sqrt{2}-4-\sqrt{2}=1\)
=1 nha
t.i.c.k mình nha
bạn nào 10sp gúp mình đi

\(\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+\sqrt{16}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\frac{\sqrt{2}+\sqrt{3}+2+2+\sqrt{2}\sqrt{3}+\sqrt{2}\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=\frac{\left(1+\sqrt{2}\right)\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=1+\sqrt{2}\)

\(x=\left(\sqrt{10}-\sqrt{6}\right)\sqrt{4+\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8+2\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)\)
\(=2\)
Với \(x=2\):
\(\frac{\sqrt{\frac{1}{x}+4+4x}}{\sqrt{x}\left(2x^2-x-1\right)}=\frac{\sqrt{\frac{1}{2}+4+8}}{\sqrt{2}\left(8-2-1\right)}=\frac{1}{2}\)

Gọi vận tốc dòng nước là \(x\left(km/h\right),0< x< 20\).
Vận tốc của cano khi đi xuôi dòng là: \(20+x\left(km/h\right)\).
Vận tốc của cano khi đi ngược dòng là: \(20-x\left(km/h\right)\)
Theo bài ra, ta có phương trình:
\(\frac{30}{20+x}+\frac{24}{20-x}=3\)
\(\Leftrightarrow\frac{30\left(20-x\right)+24\left(20+x\right)}{\left(20+x\right)\left(20-x\right)}=\frac{3\left(20+x\right)\left(20-x\right)}{\left(20+x\right)\left(20-x\right)}\)
\(\Rightarrow200-10x+160+8x=400-x^2\)
\(\Leftrightarrow x^2-2x-40=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1+\sqrt{41}\left(tm\right)\\x=1-\sqrt{41}\left(l\right)\end{cases}}\)


ĐK: \(0\le x\le1\).
Ta có:
với \(0\le x\le1\)thì \(0\le1-x\le1\Leftrightarrow\sqrt{1-x}\left(1-\sqrt{1-x}\right)\ge0\Leftrightarrow\sqrt{1-x}\ge1-x\)
do đó \(x+\sqrt{1-x}\ge x+1-x=1\Rightarrow\sqrt{x+\sqrt{1-x}}\ge1\).
Do đó để phương trình đã cho có nghiệm thì:
\(\hept{\begin{cases}\sqrt{x}=0\\x+\sqrt{1-x}=1\end{cases}}\Leftrightarrow x=0\left(tm\right)\).
ĐK: \(y\ne0,xy\ge0\).
\(4x^2+9y^2=16xy\)
Chia cả hai vế cho \(y^2\)ta được:
\(4\left(\frac{x}{y}\right)^2+9=\frac{16x}{y}\)
\(\Leftrightarrow\frac{x}{y}=\frac{4\pm\sqrt{7}}{2}\)
Với \(y>0\)thì \(x\ge0\)
\(P=\frac{\sqrt{xy}+\sqrt{y^2}}{y}-\sqrt{\frac{x}{y}}=\frac{\sqrt{x}\sqrt{y}+y}{y}-\sqrt{\frac{x}{y}}=\sqrt{\frac{x}{y}}+1-\sqrt{\frac{x}{y}}=1\)
Với \(y< 0\)thì \(x\le0\):
\(P=\frac{\sqrt{xy}+\sqrt{y^2}}{y}-\sqrt{\frac{x}{y}}=\frac{\sqrt{-x}\sqrt{-y}-y}{y}-\sqrt{\frac{x}{y}}=-\sqrt{\frac{x}{y}}-1-\sqrt{\frac{x}{y}}=-2\sqrt{\frac{x}{y}}-1\)
\(=-2\sqrt{\frac{4\pm\sqrt{7}}{2}}-1=-\left(1\pm\sqrt{7}\right)-1=-2\pm\sqrt{7}\)