Ta có thể dùng cosy hoặc đặt a,b lần lượt là hai số hạng vế trái của phương, đưa phương trình về hệ phương trình không triệt để. Từ đó giải phương.

Đầu kiện: \(x\ge0\)

Ta có:

\(4\sqrt{x}=2\sqrt{4x}\le4+x\\ \Rightarrow x^2+4-4\sqrt{x}\ge x^2-x\\ \Rightarrow\sqrt{x^2+4-4\sqrt{x}}\ge\sqrt{x^2-x}\) 

\(6\sqrt{x}=2\sqrt{9x}\le9+x\\ \Rightarrow\sqrt{x^2+4-6\sqrt{x}}\ge\sqrt{x^2-x-5}\)

Suy ra \(1\ge\sqrt{x^2-x}+\sqrt{x^2-x-5}\)

Đặt \(\sqrt{x^2-x}=a;0\le a\le1\\ \sqrt{x^2-x-5}=b;0\le b\le1.\\ \Rightarrow a^2-b^2=\left(x^2-x\right)-\left(x^2-x-5\right)=5.Vôlí\)

Vậy phương trình đã cho vô nghiệm.

a.

Số 2 ở hàng đơn vị trong dãy số trên là dãy số: \(22;32;42;...;292;302\)

Số chữ số 2 ở hàng đơn vị trong dãy số trên bằng: \(\dfrac{302-22}{10}+1=29.số\)

Số 2 được viết ở hàng trục trong dãy số trên là dãy số:\(20;22;24;26;28;\\ 120;122;124;126;128;\\ 220;222;224;226;228\)

Số chữ số 2 được viết ở hàng trục là: \(5\times3=15.số\)

Số 2 được viết ở hàng trăm là dãy số: \(200;202;204;....;296;298\)

Số chữ số 2 được dùng ở hàng trăm trong dãy số trên là: \(\dfrac{298-200}{2}+1=50.số\)

Số chữ số 2 được dùng trong dãy số đã cho là: \(29+15+50=94.số\)

b.

Dãy số \(14;16;18;...;98\) cần dùng số chữ số để viết là: \(\left(\dfrac{98-14}{2}+1\right)\times2=86\)

Để viết được 366 chữ số ta cần dùng thêm các số có 3 chữ số để viết thêm: \(366-86=280.số\)

Ta có \(280:3=93.dư.1\)

Vậy chữ số 366 là chữ số hàng trăm của số thứ 94 trong dãy: \(100;102;....;304\)

Số thứ 94 trong dãy trên bằng: \(\left(94-1\right)\times2+100=286\)

Chữ số 366 trong dãy số đã cho là chữ số 2.

Đầu kiện: \(x+y\ne0\Leftrightarrow x\ne-y\)

Ta có:

\(3x^3-y^3=\dfrac{1}{x+y}\\ \Leftrightarrow\left(3x^3-y^3\right)\left(x+y\right)=1\\ \Leftrightarrow\left(3x^3-y^3\right)\left(x+y\right)=\left(x^2+y^2\right)^2\)(*)

Xét \(y=0\Rightarrow x=\pm1\) thay vào phương trình (*) ta thấy không thõa mãn.

Với \(y\ne0\) chia hai vế phương trình (*) cho \(y^4\) ta có:

\(\dfrac{\left(3x^3-y^3\right)\left(x+y\right)}{y^4}=\dfrac{\left(x^2+y^2\right)^2}{y^4}\\ \Leftrightarrow\left(\dfrac{3x^3}{y^3}-1\right)\left(\dfrac{x}{y}+1\right)=\left(\dfrac{x^2}{y^2}+1\right)^2\)

Đặt \(t=\dfrac{x}{y}\) thay vào phương trình trên ta có:

\(\left(3t^3-1\right)\left(t+1\right)=\left(t^2+1\right)^2\)

\(\Leftrightarrow3t^4-t+3t^3-1=t^4+2t^2+1\\ \Leftrightarrow2t^4+3t^3-2t^2-t-2=0\\ \)

\(\Leftrightarrow2t^3\left(t+2\right)-t^2\left(t+2\right)-\left(t+2\right)=0\\ \Leftrightarrow\left(t+2\right)\left(2t^3-t^2-1\right)=0\\ \Leftrightarrow\left(t+2\right)\left(t^3-1+t^3-t^2=0\right)\\ \Leftrightarrow\left(t+2\right)\left(t-1\right)\left(2t^2+t+1\right)=0\\ \)

\(\Rightarrow\left[{}\begin{matrix}t+2=0\\t-1=0\\2t^2+t+1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}t=-2\\t=1\\\Delta< 0,vô.nghiệm\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-2y\\x=y\end{matrix}\right.\)

Thay x vào phương trình \(x^2+y^2=1\) tìm y => x.

So với đầu kiện bài toán kết luận nghiệm

Với `x \ne 0,x \ne 1` có:

`A=([x\sqrt{x}]/[\sqrt{x}-1]-[x^2]/[x\sqrt{x}])(1/\sqrt{x}-1)^2`

`A=([x\sqrt{x}]/[\sqrt{x}-1]-x/\sqrt{x})([1-\sqrt{x}]/\sqrt{x})^2`

`A=[x^2-x(\sqrt{x}-1)]/[\sqrt{x}(\sqrt{x}-1)].[(\sqrt{x}-1)^2]/x`

`A=[x(x-\sqrt{x}-1)]/\sqrt{x}.[\sqrt{x}-1]/x`

`A=[x-\sqrt{x}-1]/[\sqrt{x}-1]`

`a)`Ta có: \(\left\{{}\begin{matrix}AB\perp AC\\HE\perp AC\end{matrix}\right.\) \(\Rightarrow\)`AB////HE`

`b)`Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)

\(\Rightarrow\widehat{C}=180^o-90^o-60^o=30^o\)

Xét tam giác AHC, có:

\(\widehat{HAC}=180^o-30^o-90^o=60^o\)

\(\widehat{A}=\widehat{BAH}+\widehat{HAC}\)

\(\Rightarrow\widehat{BAH}=90^o-60^o=30^o\)

Ta có: \(\widehat{BAH}=\widehat{AHE}=30^o\) ( so le trong )

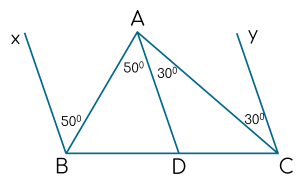
Vì \(\widehat{xBA}=\widehat{BAD}\left(=50^o\right)\) mà \(\widehat{xBA}\text{ và }\widehat{BAD}\) là 2 góc so le trong

=> Bx//AD (1)

Vì \(\widehat{DAC}=\widehat{ACy}\left(=30^o\right)\) mà \(\widehat{DAC}\text{ và }\widehat{ACy}\) là 2 góc so le trong

=> AD // Cy (2)

Từ (1) và (2) => Bx // Cy

Ta có:

`@` \(\widehat{ABx}=\widehat{DAB}=50^o\)

`=>Bx////AD` ( 2 góc so le trong bằng nhau ) (1)

`@`\(\widehat{ACy}=\widehat{DAC}=30^o\)

`=>Cy////AD` ( 2 góc so le trong bằng nhau ) (2)

\(\left(1\right);\left(2\right)\Rightarrow\)`Bx////Cy`

số tiền lãi mà mẹ minh được nhận sau 6 tháng là

2062400 - 2000000 = 62400 (đồng)

mỗi tháng số tiền lãi mà mẹ minh nhận được là

62400 : 6 = 10400 (đồng)

% lãi hàng tháng là 

10400 : 2000000 x 100 = 0,52% 

đs....

số tiền lãi mà mẹ minh được nhận sau 6 tháng là

2062400 - 2000000 = 62400 (đồng)

mỗi tháng số tiền lãi mà mẹ minh nhận được là

62400 : 6 = 10400 (đồng)

% lãi hàng tháng là 

10400 : 2000000 x 100 = 0,52% 

\(Q=-2\sqrt{x-3}+1\le1\)

Dấu ''='' xảy ra khi x = 3 

.

a + b, A=\(\dfrac{x-3\sqrt{x}+2}{x-4\sqrt{x}+3}\) = \(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}\)=\(\dfrac{\sqrt{x}-2}{\sqrt{x}-3}\)

ĐKXĐ: \(\sqrt{x}-3\)\(\Leftrightarrow\sqrt{x}\)\(\ne\)3\(\Leftrightarrow\) x\(\ne\)9

 

c, \(\dfrac{\sqrt{x}-2}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3+1}{\sqrt{x}-3}=1+\dfrac{1}{\sqrt{x}-3}\Rightarrow\sqrt{x}-3\inƯ\left(1\right)=\left\{\pm1\right\}\)