Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5 + 2x = x - 5
<=> 2x - x = -5 - 5
<=> x = -10
Vậy pt có nghiệm x = -10


1.Gọi n là số ngày chị Mai làm theo kế hoạch
---> Số dụng cụ làm theo kế hoạch là 20n
Theo đề ra ta có 20n = (n - 2)25 - 10
=>20n=25n-50-10
=>20n=25n-60
=>5n=60
=>n=12
=>số ngày chị Mai làm theo kế hoạch là 12
mà mỗi ngày chị phải làm 20 dụng cụ
Vậy số dụng cụ chị Mai làm theo kế hoạch là:20*12=240 (dụng cụ)

\(B=\frac{\left(x-2\right)^2+2016}{\left(x-1\right)^2}=\frac{\left(t-1\right)^2+2016}{t^2}=\frac{t^2-2t+2017}{t^2}\)
\(=1-\frac{2}{t}+\frac{2017}{t^2}=1-2a+2017a^2=2017\left(a^2-2.\frac{1}{4034}+\frac{1}{4034}^2\right)-\frac{2017}{4034^2}+1\)
\(=2017\left(a-\frac{1}{4034}\right)^2+1-\frac{1}{2017^3}\ge1-\frac{1}{2017^3}\)
tự xét dấu =
\(B=\frac{\left(x-2\right)^2+2016}{\left(x-1\right)^2}\)
\(\Leftrightarrow\frac{\left(t-1\right)^2+2016}{1^2}\)
\(\Leftrightarrow\frac{t^2-2t+2017}{t^2}\)
\(\Leftrightarrow1-\frac{2}{t}+\frac{2017}{t^2}\)
\(\Leftrightarrow1-2a+2017a^2\)
\(\Leftrightarrow a^2-2\times[\frac{1}{4034}+\frac{1^2}{4034}]-\frac{2017}{4034^2}+1\)
\(\Leftrightarrow2017\left(a-\frac{1}{4034}\right)^2+1-\frac{1}{2017}^3\)
phần cuối tự làm nha

A B C P M N D E F
a) Ta có ^APB = ^BAC/2 + ^ABC/2 + ^ACB = 900 + ^ACB/2 = ^AMP; ^BAP = MAP
Suy ra \(\Delta\)AMP ~ \(\Delta\)APB (g.g) => \(\frac{AM}{PM}=\frac{AP}{BP}\). Tương tự \(\frac{PN}{BN}=\frac{AP}{BP}\)
Từ đó \(\frac{AM}{BN}.\frac{PN}{PM}=\left(\frac{AP}{BP}\right)^2\). Dễ thấy PM = PN, vậy \(\frac{AM}{BN}=\left(\frac{AP}{BP}\right)^2\)
b) Theo hệ thức lượng và tam giác đồng dạng, ta có biến đổi sau:
\(\frac{AM}{AC}+\frac{BN}{BC}+\frac{CP^2}{BC.AC}\)
\(=\frac{AM}{AP}.\frac{AP}{AC}+\frac{BN}{BP}.\frac{BP}{BC}+\frac{CP^2}{BC.AC}\)
\(=\frac{AP^2}{AB.AC}+\frac{BP^2}{BA.BC}+\frac{CP^2}{CA.CB}\)
\(=\frac{AP^2.BC+BP^2.CA+CP^2.AB}{BC.CA.AB}\)
\(=\frac{AP^2.\sin A+BP^2.\sin B+CA^2.\sin C}{2S}\)(S là diện tích tam giác ABC)
\(=\frac{AP^2.\sin\frac{A}{2}.\cos\frac{A}{2}+BP^2.\sin\frac{B}{2}.\cos\frac{B}{2}+CP^2.\sin\frac{C}{2}.\cos\frac{C}{2}}{S}\)
\(=\frac{FA.FP+DB.DP+EC.EP}{S}=\frac{dt\left[AFPE\right]+dt\left[BDPF\right]+dt\left[CEPD\right]}{S}=1.\)


M N P 3 4 H D K
a, Xét tam giác NMP vuông tại M, có đường cao MH
Áp dụng định lí Py ta go ta có :
\(NP^2=MN^2+MP^2=9+16=25\Rightarrow NP=5\)cm
Vì ND là đường phân giác nên : \(\frac{MN}{NP}=\frac{MD}{DP}\)mà \(DP=MP-MD=4-MD\)
hay \(\frac{3}{5}=\frac{MD}{4-MD}\Rightarrow12-3MD=5MD\)
\(\Leftrightarrow8MD=12\Leftrightarrow MD=\frac{12}{8}=\frac{3}{2}\)cm
b, Xét tam giác MHN và tam giác MNP ta có :
^NHM = ^NMP = 900
^N _ chung
Vậy tam giác MHN ~ tam giác MNP ( g.g )
c, Xét tam giác NDM và tam giác NKH ta cs :
^MNP = ^NHK = 900
\(\frac{MN}{NH}=\frac{MK}{KH}\)( NK là đường phân giác )
Vậy tam giác NDM ~ tam giác NKH ( c.g.c )
\(\Rightarrow\frac{ND}{NK}=\frac{NM}{NH}\)( tỉ số đồng dạng ) \(\Rightarrow ND.NH=NM.NK\)
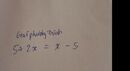

Gọi độ dài 1 cạnh hình vuông là x ( m ; x > 0 )
=> Diện tích hình vuông ban đầu = x2 ( m2 )
Tăng một cạnh lên 5m và giảm cạnh liền đi 3m thì được hình chữ nhật có diện tích > diện tích hình vuông 9m2
=> Ta có phương trình : x2 + 9 = ( x + 5 )( x - 3 )
<=> x2 + 9 = x2 + 2x - 15
<=> -2x = -24 <=> x = 12 (tm)
Vậy ...