Lời giải của Le Minh Huy:
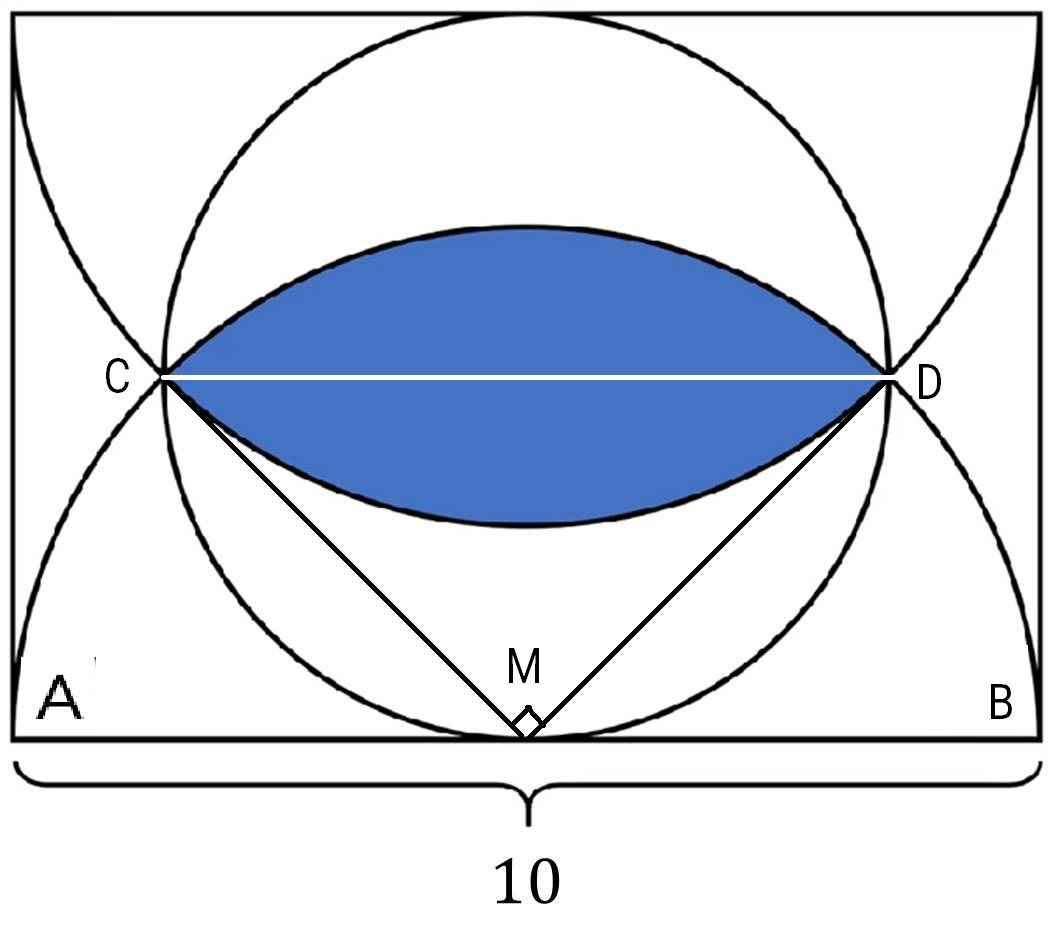
Ta có: MC = MD = MA =10/2 = 5(đvđd)(cùng là bán kính của đường tròn tâm M)
Vì ΔMCD nội tiếp hình tròn có tâm là trung điểm của CD nên \(\widehat{CMD}=90^O\)
Diện tích hình quạt tròn cung \(90^o\) giới hạn bởi MC và MD là: \(S=\dfrac{\pi R^2n}{360}=\dfrac{\pi\cdot5^2\cdot90}{360}=\dfrac{25\pi}{4}\left(đvdt\right)\)
Diện tích ΔMCD là: \(S_{MCD}=\dfrac{5\cdot5}{2}=\dfrac{25}{2}\left(dvdt\right)\)
Một nửa phần được tô màu có diện tích là: \(S_1=S-S_{MCD}=\dfrac{25}{4}\pi-\dfrac{25}{2}\left(đvdt\right)\)
Vậy diện tích phần được tô màu là: \(2S_1=\dfrac{25}{2}\pi-25\left(đvdt\right)\)
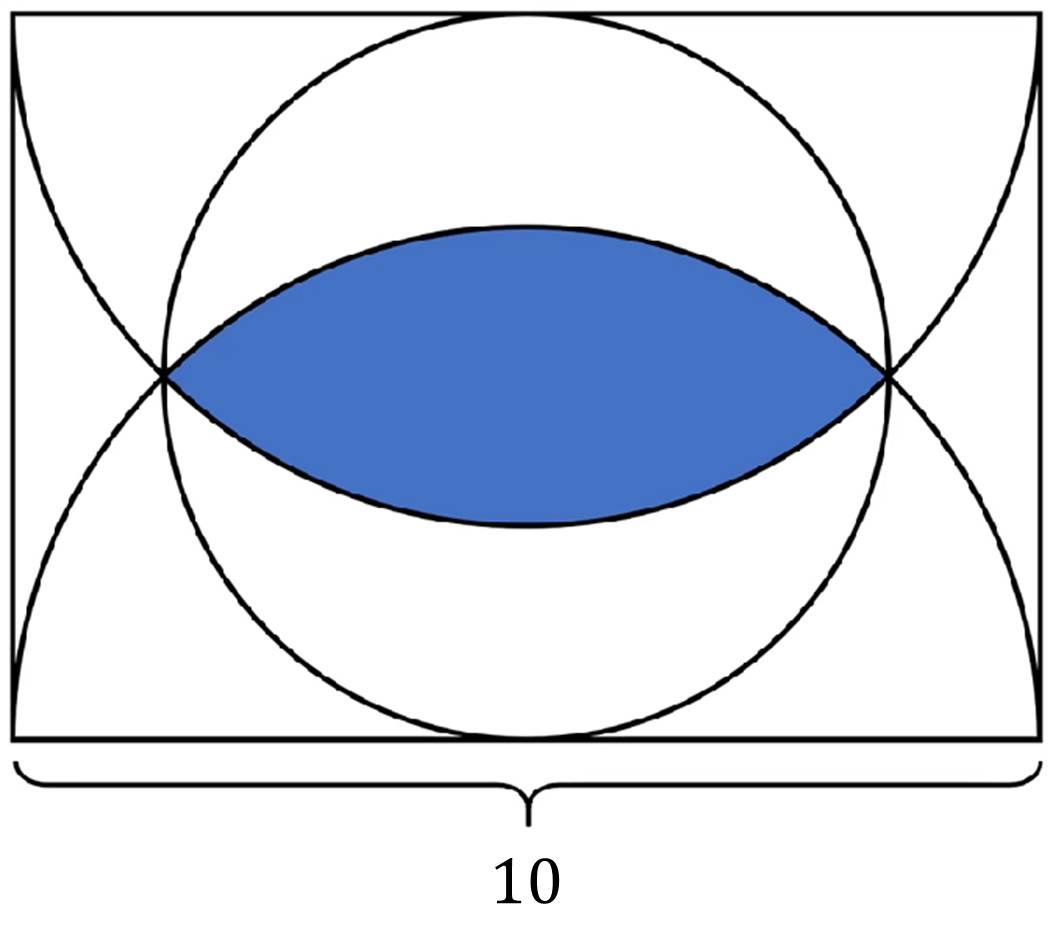
Dựa vào hình trên, tính diện tích phần được tô màu xanh dương.
-------------------------
Các bạn nhấn vào nút Tham dự bài thi bên dưới để trình bày lời giải đầy đủ của mình. Mười bạn có lời giải hay và sớm nhất sẽ được cộng/thưởng 2 tháng VIP của Online Math. Giải thưởng sẽ được công bố vào Thứ Sáu ngày 6/5/2022. Câu đố tiếp theo sẽ lên mạng vào Thứ Sáu ngày 6/5/2022.

