Xét tính đơn điệu của hàm số SVIP

Cho hàm số $y=f'(x)$ có bảng xét dấu như sau:

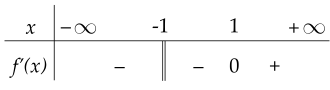
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Cho hàm số $y=f\left(x \right)$ có bảng biến thiên như sau:

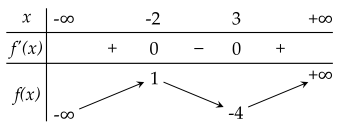
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Cho hàm số $y=f\left(x \right)$ có đồ thị như hình vẽ.

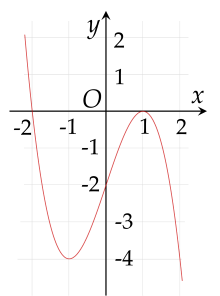
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=x+1$, $\forall x\in \mathbb{R}$. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Cho hàm số $y=f(x)$ có đạo hàm $f'(x) = x^2 + 16$. Khi đó, hàm số $y=f(x)$ luôn

Hàm số nào sau đây đồng biến trên khoảng $\big(-\infty ; + \infty\big)$?

Hàm số $y=\dfrac{5-2x}{x+3}$ nghịch biến trên khoảng nào dưới đây?

Cho hàm số $y=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-12x-1$. Mệnh đề nào sau đây đúng?

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

Hàm số $y=x^3 - 2x^2 + x + 1$ nghịch biến trên khoảng nào dưới đây?