Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Vẽ đồ thị hàm số $y = ax^2$ ($a \ne 0$) SVIP
Cho hàm số $y=2x^2$.
a) Vẽ đồ thị của hàm số $y=2x^2$.
b) Các điểm $M( -4;32 )$, $N\Big( -\dfrac{1}{2};\dfrac{1}{2} \Big)$, $Q\Big( \dfrac{3}{4};\dfrac{9}{16} \Big)$ có thuộc đồ thị hàm số hay không?
Hướng dẫn giải:
Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=2x^2$ | $8$ | $2$ | $0$ | $2$ | $8$ |
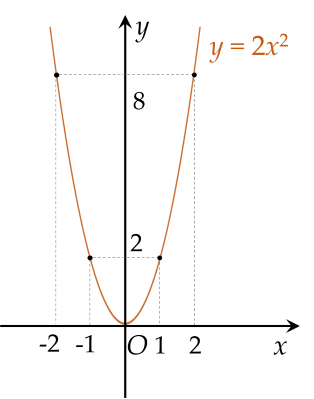
Vẽ các điểm $A( -2;8 )$, $B( -1;2 )$, $O( 0;0 )$, $C( 1;2 )$, $D( 2;8 )$ thuộc đồ thị hàm số $y = 2x^2$ trong mặt phẳng $Oxy$.
Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y = 2x^2$.
b)
+ Thay $x=-4$ vào đồ thị của hàm số $y = 2x^2$ ta được: $y=2.(-4)^2=32$,
Do đó điểm $M( -4;32 )$ thuộc đồ thị hàm số đã cho.
+ Thay $x=-\dfrac12$ vào đồ thị của hàm số $y = 2x^2$ ta được: $y=2.\Big( -\dfrac{1}{2} \Big)^2=\dfrac12$,
Do đó điểm $N\Big( -\dfrac{1}{2};\dfrac{1}{2} \Big)$ thuộc đồ thị hàm số đã cho.
+ Thay $x=\dfrac{3}{4}$ vào đồ thị của hàm số $y = 2x^2$ ta được: $y=2.\Big( \dfrac{3}{4} \Big)^2=\dfrac{9}{8}\ne \dfrac{9}{16}$,
Do đó điểm $Q\Big( \dfrac{3}{4};\dfrac{9}{16} \Big)$ không thuộc đồ thị hàm số đã cho.
Cho hàm số $y=-\dfrac14x^2$ có đồ thị $(P)$.
a) Vẽ đồ thị $(P)$.
b) Các điểm $E( -8;-16 )$, $F\Big( -\dfrac{1}{3};-\dfrac{1}{36} \Big)$, $Q\Big( \dfrac{2}{5};\dfrac{4}{100} \Big)$ có thuộc đồ thị hàm số hay không?
Hướng dẫn giải:
Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-4$ | $-2$ | $0$ | $2$ | $4$ |
| $y = -\dfrac14x^2$ | $-4$ | $-1$ | $0$ | $-1$ | $-4$ |
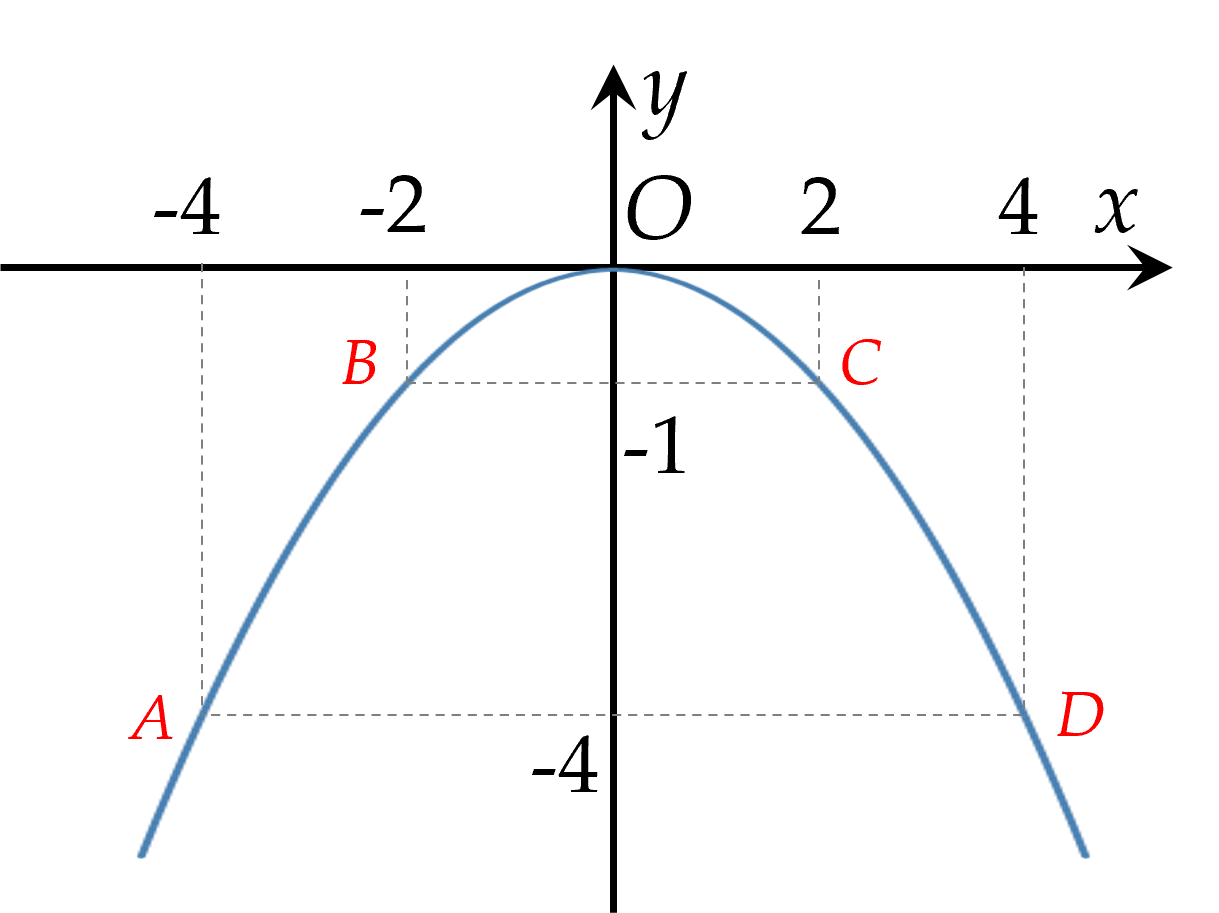
Vẽ các điểm $A( -4;-4 ),$ $B( -2;-1 )$, $O( 0;0 ),$ $C( 2;-1 ),$ $D( 4;-4 )$ thuộc đồ thị hàm số $y=-\dfrac14x^2$ trong mặt phẳng $Oxy$.
Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y=-\dfrac14x^2$.
b)
- Thay $x=-8$ vào đồ thị của hàm số $y=-\dfrac14x^2$ ta được: $y=-\dfrac14(-8)^2=-16$,
Do đó điểm $E( -8;-16 )$ thuộc đồ thị hàm số đã cho.
- Thay $x=-\dfrac13$ vào đồ thị của hàm số $y=-\dfrac14x^2$ ta được: $y=-\dfrac14\Big( -\dfrac{1}{3} \Big)^2=-\dfrac{1}{36}$,
Do đó điểm $F\Big( -\dfrac{1}{3};-\dfrac{1}{36} \Big)$ thuộc đồ thị hàm số đã cho.
- Thay $x=\dfrac{2}{5}$ vào đồ thị của hàm số $y=-\dfrac14x^2$ ta được: $y=-\dfrac14\Big( \dfrac{2}{5} \Big)^2=-\dfrac{4}{100} \ne \dfrac{4}{100}$,
Do đó điểm $Q\Big( \dfrac{2}{5};\dfrac{4}{100} \Big)$ không thuộc đồ thị hàm số đã cho.
Cho hàm số $y=\dfrac12x^2$.
a) Vẽ đồ thị của hàm số $y=\dfrac12x^2$.
b) Các điểm $M\Big( -5;-\dfrac{25}{2} \Big)$, $N\Big( -\dfrac{3}{2};\dfrac{9}{8} \Big)$, $Q\Big( \dfrac{1}{2};2 \Big)$ có thuộc đồ thị hàm số hay không?
Hướng dẫn giải:
- Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-4$ | $-2$ | $0$ | $2$ | $4$ |
| $y = \dfrac12x^2$ | $8$ | $2$ | $0$ | $2$ | $8$ |
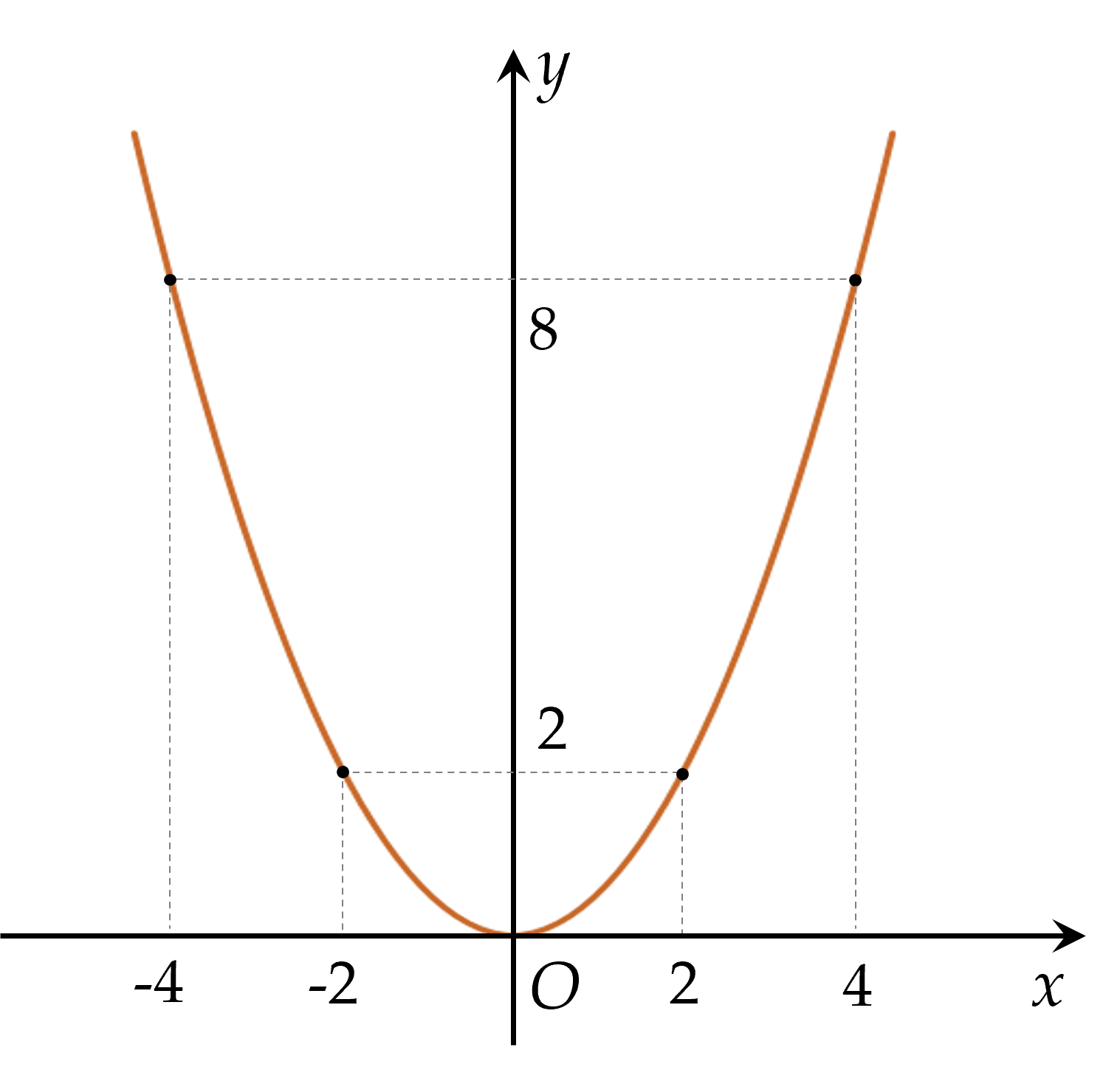
- Vẽ các điểm $A( -4;8 ), \, B( -2;2 ), \, O( 0;0 ), \, C( 2;2 ), \, D( 4;8 )$ thuộc đồ thị hàm số $y=\dfrac12x^2$ trong mặt phẳng $Oxy$.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y=\dfrac12x^2$.
b)
- Thay $x=-5$ vào đồ thị của hàm số $y=\dfrac12x^2$ ta được: $y=\dfrac{1}{2}.(-5)^2=\dfrac{25}{2}\ne -\dfrac{25}{2}$,
Do đó điểm $M\Big( -5;-\dfrac{25}{2} \Big)$ không thuộc đồ thị hàm số đã cho.
- Thay $x=-\dfrac{3}{2}$ vào đồ thị của hàm số $y=\dfrac12x^2$ ta được: $y=\dfrac{1}{2}.\Big( -\dfrac{3}{2} \Big)^2=\dfrac{9}{8}$,
Do đó điểm $N\Big( -\dfrac{3}{2};\dfrac{9}{8} \Big)$ thuộc đồ thị hàm số đã cho.
- Thay $x=\dfrac{1}{2}$ vào đồ thị của hàm số $y=\dfrac12x^2$ ta được: $y=\dfrac{1}{2}.\Big( \dfrac{1}{2} \Big)^2=\dfrac{1}{8}\ne 2$,
Do đó điểm $Q\Big( \dfrac{1}{2};2 \Big)$ không thuộc đồ thị hàm số đã cho.
Cho đồ thị hàm số $y=x^2$ có đồ thị $(P)$.
a) Vẽ đồ thị $(P)$.
b) Tìm các điểm trên Parabol có tung độ bằng $16$.
c) Tìm các điểm trên Parabol (khác gốc tọa độ) cách đều hai trục tọa độ.
Hướng dẫn giải:
- Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:
| $x$ | $-2$ | $-1$ | $0$ | $1$ | $2$ |
| $y=x^2$ | $4$ | $1$ | $0$ | $1$ | $4$ |
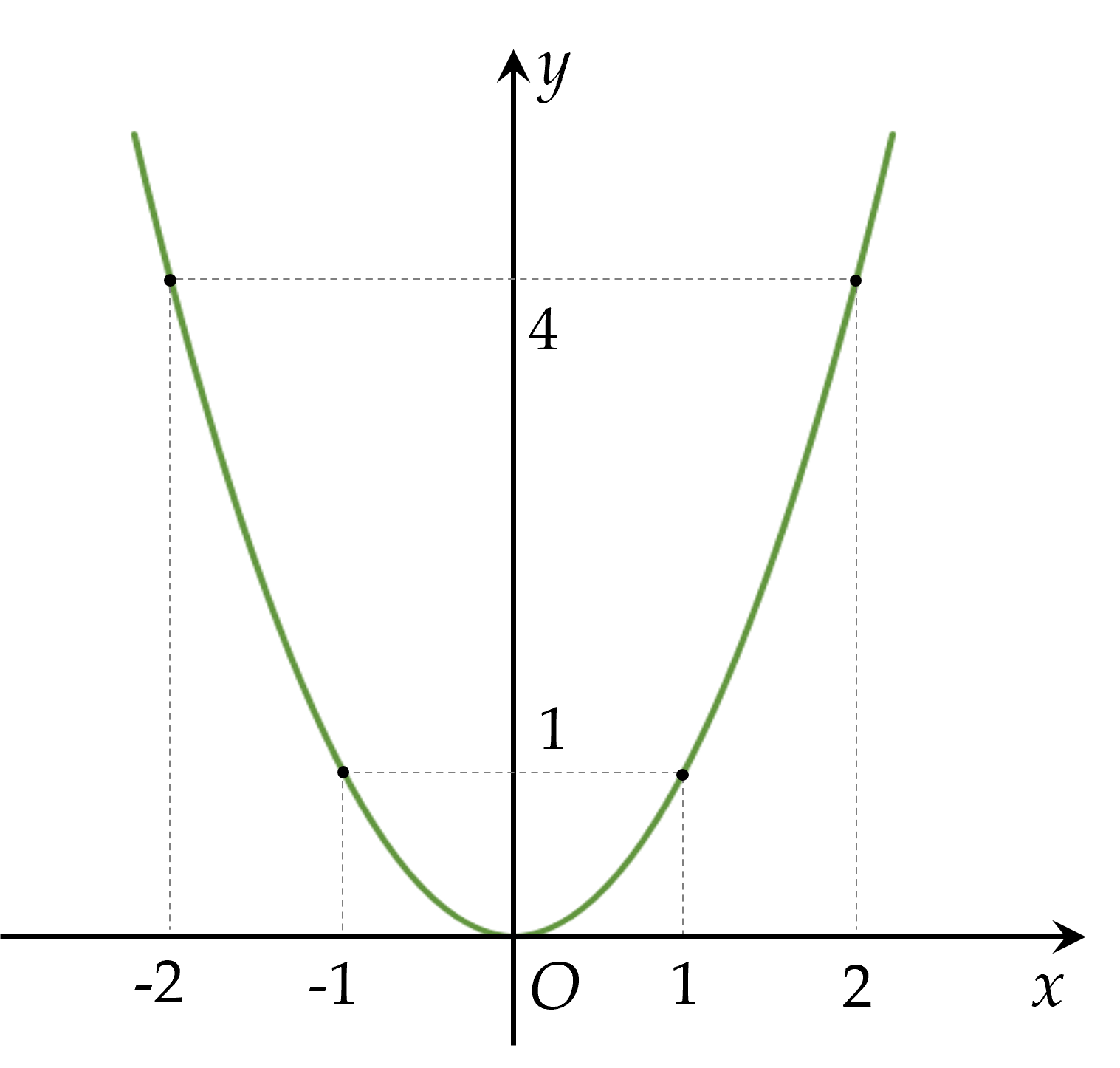
- Vẽ các điểm $A( -2;4 ), \, B( -1;1 ), \, O( 0;0 ), \, C( 1;1 ), \, D( 2;4 )$ thuộc đồ thị hàm số $y=x^2$ trong mặt phẳng $Oxy$.
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y=x^2$.
b) Gọi $C$ là điểm thuộc $(P)$ có tung độ bằng $16$.
Ta có: $y_C=16$ hay $(x_C)^2=16$ suy ra $x_C=\pm 4$.
Vậy $C( 4;16 )$ hoặc $C( -4;16 )$.
c) Gọi $D$ là điểm thuộc $(P)$ cách đều hai trục tọa độ.
Ta có: $d\left( D,Ox \right)=\left| y_D \right|=x_{D}^{2};$
$d\left( D,Oy \right)=\left| x_D \right|$.
Theo giả thiết ta có: $x_{D}^{2}=\left| x_D \right|$ suy ra $\left| x_D \right|=0$ (loại) hoặc $\left| x_D \right|=1$.
Vậy $D( 1;1 )$ hoặc $D( -1;1 )$.
