Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Ứng dụng tích phân để tính diện tích hình phẳng SVIP
Cho hàm số y=f(x) xác định và liên tục trên đoạn. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a,x=b được tính theo công thức nào?
Cho hàm số y=f(x) và y=g(x) có đồ thị như hình vẽ:
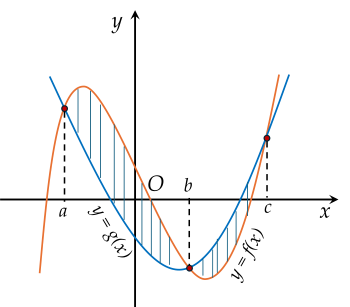
Diện tích S của phần gạch chéo trong hình vẽ trên được tính bằng công thức là
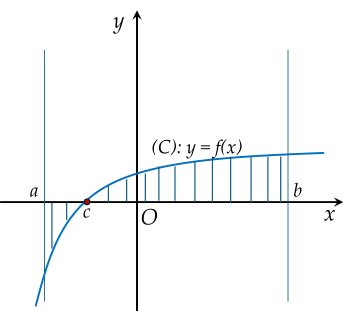
Diện tích hình phẳng (H) được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a,x=b (a<b) (phần gạch chéo như hình vẽ) được tính theo công thức nào?
Diện tích S hình phẳng giới hạn bởi các đường y=2x2, y=−1, x=0 và x=1 là
Diện tích hình phẳng giới hạn bởi hai đường y=x2 và y=x là
Cho hình phẳng (D) giới hạn bởi đồ thị của ba hàm số y=f(x), y=g(x), y=h(x) như hình bên dưới:

Diện tích hình phẳng (D) là
Diện tích hình phẳng giới hạn bởi parabol y=x2 và đường thẳng y=3x−2 là
Cho đường thẳng y=x−a (a là tham số thực dương) và đồ thị hàm số y=x. Gọi S1,S2 lần lượt là diện tích hai hình phẳng được gạch chéo trong hình vẽ dưới đây:
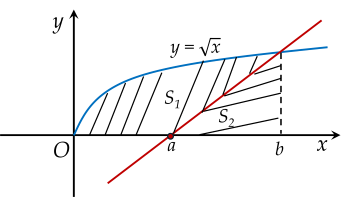
Khi S1=35S2 thì a bằng bao nhiêu?
Trả lời:
Cho đồ thị hàm số y=f(x) và y=g(x) như hình vẽ bên dưới:
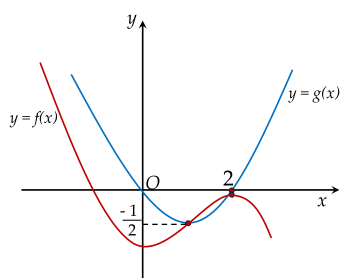
Biết đồ thị của hàm số y=g(x) là một Parabol đỉnh I có tung độ bằng −21 và y=f(x) là một hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là x1,x2,x3 thỏa mãn x1.x2.x3=−6. Diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số y=f(x) và y=g(x) gần nhất giá trị nguyên nào?
Trả lời:
Cho hàm số y=f(x) liên tục trên đoạn [0;8] và có đồ thị như hình vẽ:
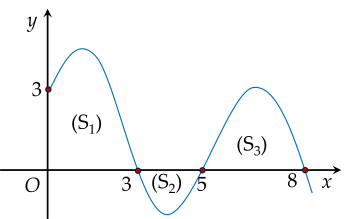
| a) S1=∫03f(x)dx. |
|
| b) S2+S3=∫38f(x)dx. |
|
| c) S1−S2=−∫05f(x)dx. |
|
| d) ∫08f(x)dx>∫58f(x)dx. |
|
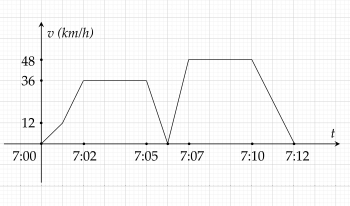
Anh Đức đi làm lúc 7 giờ và đến cơ quan lúc 7 giờ 12 phút bằng xe gắn máy, trên đường đến cơ quan anh Đức gặp một người băng qua đường nên anh phải giảm tốc độ để đảm bảo an toàn rồi sau đó lại từ từ tăng tốc độ để đến cơ quan làm việc. Hỏi quãng đường kể từ lúc anh Đức giảm tốc độ để tránh tai nạn cho đến khi tới cơ quan dài bao nhiêu mét? (Đồ thị dưới đây mô tả vận tốc chuyển động của anh Đức theo thời gian khi đến cơ quan)

Bạn có thể đăng câu hỏi về bài học này ở đây
