Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Ứng dụng của hàm số bậc hai SVIP

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Ứng dụng của hàm số bậc hai trong:
1. Tìm GTLN, GTNN của hàm số:
Cho hàm số $y = ax^2 + bx + c$, $a \ne 0$, đồ thị hàm số có tọa độ đỉnh $I\left(-\dfrac b{2a} ; -\dfrac{\Delta}{4a}\right)$.
+ Nếu $a > 0$ thì hàm số đạt giá trị nhỏ nhất là $-\dfrac{\Delta}{4a}$ khi $x = -\dfrac b{2a}$;
+ Nếu $a < 0$ thì hàm số đạt giá trị loén nhất là $-\dfrac{\Delta}{4a}$ khi $x = -\dfrac b{2a}$;
2. Bài toán thực tế: quỹ đạo chuyển động của vật thể có hình dạng parabol,...
Điểm cao nhất (hoặc thấp nhất) của đồ thị hàm số bậc hai y=ax2+bx+c với a=0 là
Xét hàm số bậc hai y=ax2+bx+c với a=0 thì biệt thức Δ=b2−4ac.
Biệt thức Δ ứng với hàm số y=−2x2−2x+4 bằng
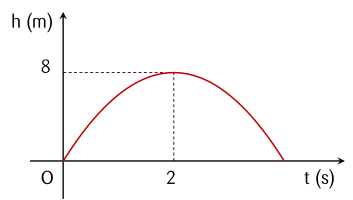
Hình trên là đồ thị của hàm số bậc hai y=ax2+bx+c với
Đồ thị hàm số h=f(t)=at2+bt với a<0 có tọa độ đỉnh (2;8) suy ra
Nghiệm (a;b) của hệ phương trình {−b=4a4a+2b=8 là
Hàm số liên hệ giữa độ cao h (m) theo thời gian t (giây) là h=f(t)=−2t2+8t.
Khi t=3 (giây) thì độ cao h là
Giá trị t thỏa mãn {t>0−2t2+8t=0 là
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
Bạn có thể đăng câu hỏi về bài học này ở đây
