Tự luận (8 điểm) SVIP

Hướng dẫn giải:

a) $A$ xác định khi $x+4\ne 0$; $x-4\ne0$; $x^2-16\ne0$

Hay $x\ne-4$; $x\ne4$.

b) Ta có: $A=\dfrac{1}{x+4}+\dfrac{x}{x-4}+\dfrac{24-x^2}{x^2-16}$

$=\dfrac{x-4}{(x-4)(x+4)}+\dfrac{x(x+4)}{(x-4)(x+4)}+\dfrac{24-x^2}{(x-4)(x+4)}$

$=\dfrac{x-4+x^2+4x+24-x^2}{(x-4)(x+4)}$

$=\dfrac{5x+20}{(x-4)(x+4)}$

$=\dfrac{5(x+4)}{(x-4)(x+4)}$

$=\dfrac{5}{x-4}$.

c) Tại $x=10$ (thoả mãn điều kiện xác định), ta có $A=\dfrac{5}{10-4}=\dfrac{5}{6}$.

Hướng dẫn giải:

a) $(x+1)(x-3)-x^2+6x-9=0$.

$x^2-3x+x-3-x^2+6x-9=0$

$4x-12=0$

$4x=12$

$x=3$.

b) $2(x+3)+4(2-2x)=2(x-2)$.

$2x+6+8-8x=2x-4$

$-6x+14=2x-4$

$-8x=-18$

$x=\dfrac{18}{8}=\dfrac{9}{4}$.

Hướng dẫn giải:

a) $6x^2-3xy =3x(2x-y)$.

b) $x^3-16x=x(x^2-16)=x(x-4)(x+4)$.

c) $x^2-y^2+4x-4y$

$=(x^2-y^2)+(4x-4y)$

$=(x-y)(x+y)+4(x-y)$

$=(x-y)(x+y+4)$.

Hướng dẫn giải:

a) Vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta nhiều nhất là năm 2020; ít nhất là năm 2015.

b) Tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước năm 2020 so với năm 2015 là:

$\dfrac{10284,2}{6944,9}.100\%=148,1\%$

Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng $148,1\% - 100\% = 48,1\%$ so với năm 2015.

Hướng dẫn giải:

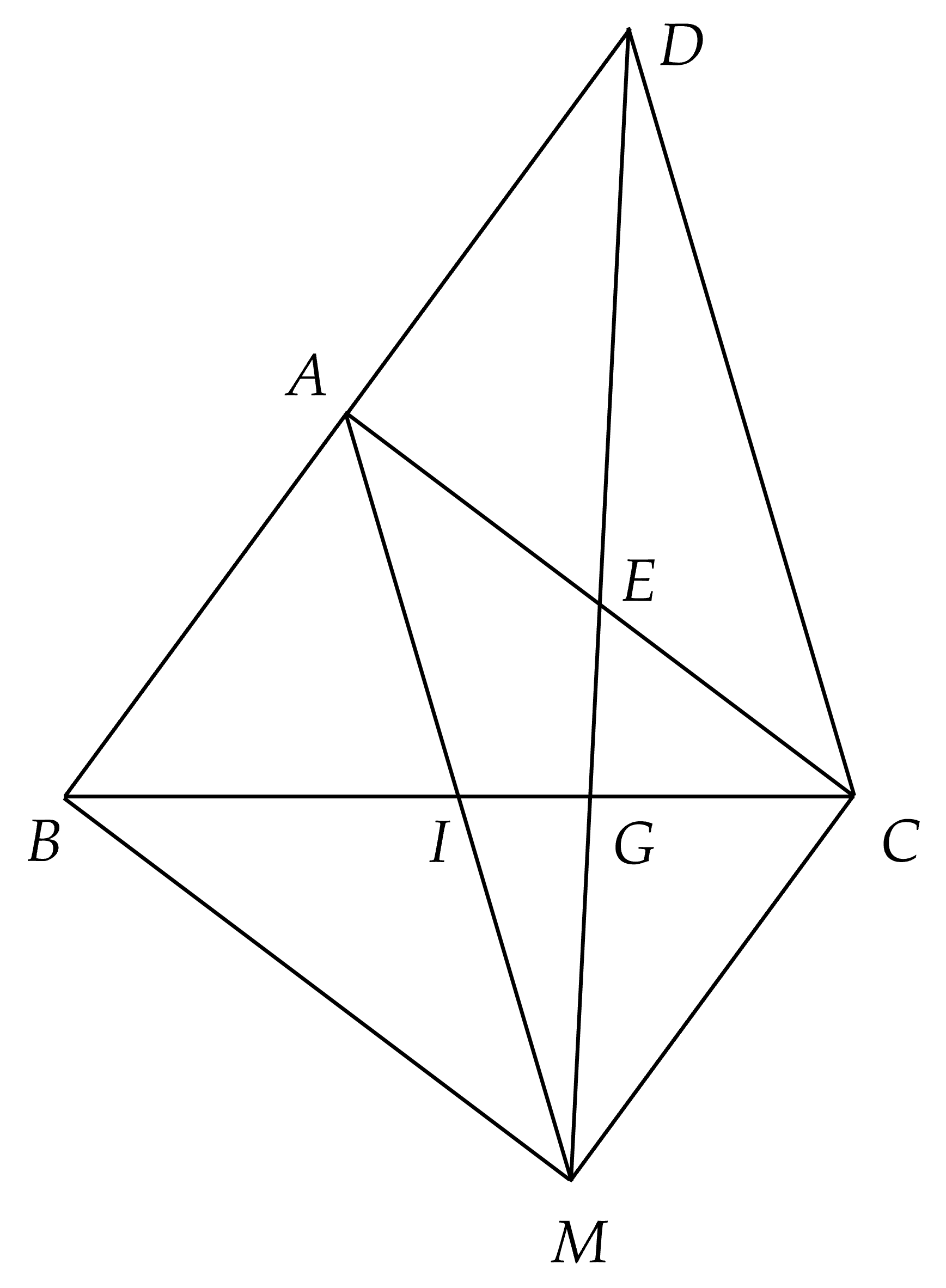
a) Xét tứ giác $ABMC$ có $AM$ cắt $BC$ tại $I$, $I$ là trung điểm của $AM$, $I$ là trung điểm của $BC$

$\Rightarrow ABMC$ là hình bình hành (dấu hiệu nhận biết).

mà $\widehat{BAC}=90^\circ$ ($\Delta ABC$ vuông tại $A$) nên $ABMC$ là hình chữ nhật (dấu hiệu nhận biết).

b) Vì $D$ đối xứng với $B$ qua $A$ nên $BA=AD$ mà $BA=CM$ (do $ABMC$ là hình chữ nhật) nên $AD=CM$ (1)

Vì $ABCD$ là hình chữ nhật  (cmt) nên $AB//CM$ hay$AD//CM$ (2)

Từ (1) và (2) ta có $AMCD$ là hình bình hành (dấu hiệu nhận biết).

c) Gọi $E$ là giao điểm của $AC$ và $DM$.

Do $AMCD$ là hình bình hành (cmt) nên $EA=EC$, $EM=ED$

Ta có:

$IM=IA \Rightarrow CI$ là đường trung tuyến của $\Delta ACM$;

$EA=EA \Rightarrow ME$ là đường trung tuyến của $\Delta ACM$

mà $IC \cap ME$ tại $G$.

Suy ra $G$ là trọng tâm của $\Delta ACM$

$\Rightarrow MG=\dfrac{2}{3}EM$.

Mà $EM=ED=\dfrac{1}{2}DM$ (cmt) 

$\Rightarrow MG = \dfrac{2}{3}. \dfrac{1}{2}DM=\dfrac{1}{3}DM$

$\Rightarrow DM=3GM$ (đpcm).

Hướng dẫn giải:

Khối lượng cá sau một vụ là

$T=(480-20n)n=-20n^2+480n$

$=-20(n^2-24n)$

$=-20(n^2-2.12n+144-144)$

$=-20(n-12)^2+2880$

Vì $-20(n-12)^2\ge 0 \,\forall n$ nên $-20(n-12)^2+2880\ge 2880 \,\forall n$ hay $T\ge 0 \,\forall n$.

Dấu bằng xảy ra khi và chỉ khi $n=12$.

Vậy phải thả $12$ con cá trên một đơn vị diện tích để khối lượng cá thu được sau một vụ là nhiều nhất.